
Question Number 188591 by 073 last updated on 03/Mar/23
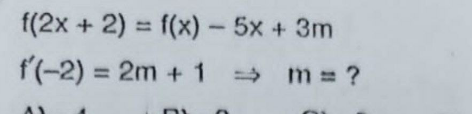
Commented by manxsol last updated on 03/Mar/23
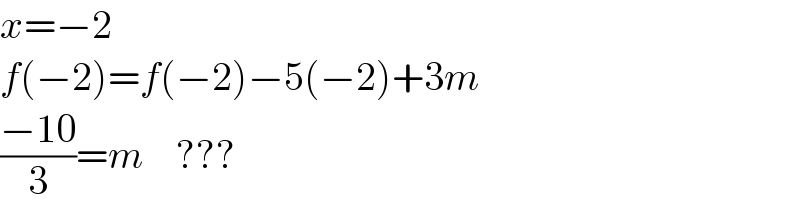
$${x}=−\mathrm{2} \\ $$$${f}\left(−\mathrm{2}\right)={f}\left(−\mathrm{2}\right)−\mathrm{5}\left(−\mathrm{2}\right)+\mathrm{3}{m} \\ $$$$\frac{−\mathrm{10}}{\mathrm{3}}={m}\:\:\:\:??? \\ $$
Commented by 073 last updated on 03/Mar/23

$$\mathrm{no} \\ $$
Commented by Frix last updated on 04/Mar/23

$$\mathrm{Yes}! \\ $$
Answered by floor(10²Eta[1]) last updated on 03/Mar/23
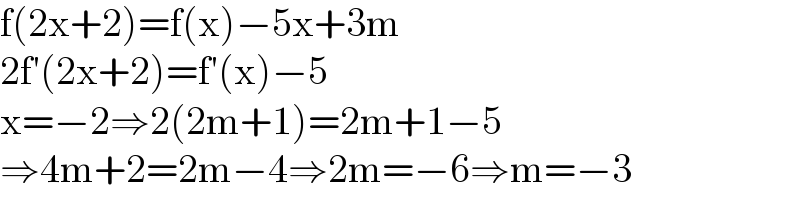
$$\mathrm{f}\left(\mathrm{2x}+\mathrm{2}\right)=\mathrm{f}\left(\mathrm{x}\right)−\mathrm{5x}+\mathrm{3m} \\ $$$$\mathrm{2f}'\left(\mathrm{2x}+\mathrm{2}\right)=\mathrm{f}'\left(\mathrm{x}\right)−\mathrm{5} \\ $$$$\mathrm{x}=−\mathrm{2}\Rightarrow\mathrm{2}\left(\mathrm{2m}+\mathrm{1}\right)=\mathrm{2m}+\mathrm{1}−\mathrm{5} \\ $$$$\Rightarrow\mathrm{4m}+\mathrm{2}=\mathrm{2m}−\mathrm{4}\Rightarrow\mathrm{2m}=−\mathrm{6}\Rightarrow\mathrm{m}=−\mathrm{3} \\ $$
Commented by 073 last updated on 03/Mar/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$
Answered by qaz last updated on 03/Mar/23
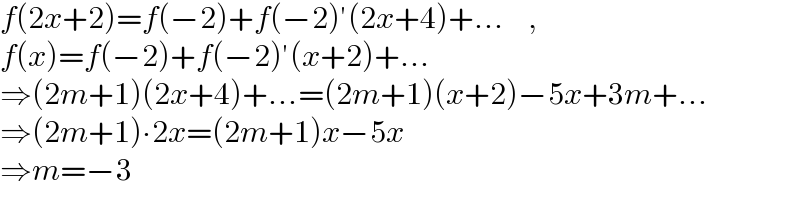
$${f}\left(\mathrm{2}{x}+\mathrm{2}\right)={f}\left(−\mathrm{2}\right)+{f}\left(−\mathrm{2}\right)'\left(\mathrm{2}{x}+\mathrm{4}\right)+...\:\:\:\:, \\ $$$${f}\left({x}\right)={f}\left(−\mathrm{2}\right)+{f}\left(−\mathrm{2}\right)'\left({x}+\mathrm{2}\right)+... \\ $$$$\Rightarrow\left(\mathrm{2}{m}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{4}\right)+...=\left(\mathrm{2}{m}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)−\mathrm{5}{x}+\mathrm{3}{m}+... \\ $$$$\Rightarrow\left(\mathrm{2}{m}+\mathrm{1}\right)\centerdot\mathrm{2}{x}=\left(\mathrm{2}{m}+\mathrm{1}\right){x}−\mathrm{5}{x} \\ $$$$\Rightarrow{m}=−\mathrm{3} \\ $$
Commented by 073 last updated on 03/Mar/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$
Answered by CElcedricjunior last updated on 03/Mar/23

$$\boldsymbol{{f}}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{2}\right)=\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)−\mathrm{5}\boldsymbol{{x}}+\mathrm{3}\boldsymbol{{m}} \\ $$$$\boldsymbol{{f}}'\left(−\mathrm{2}\right)=\mathrm{2}\boldsymbol{{m}}+\mathrm{1}\:\:\:\left(\mathrm{1}\right) \\ $$$$\boldsymbol{{calculons}}\:\boldsymbol{{m}} \\ $$$$\boldsymbol{{f}}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{2}\right)=\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)−\mathrm{5}\boldsymbol{{x}}+\mathrm{3}\boldsymbol{{m}}\:\blacksquare\mathscr{C}{edric}\:{junior} \\ $$$$=>\mathrm{2}\boldsymbol{{f}}'\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{2}\right)=\boldsymbol{{f}}'\left(\boldsymbol{{x}}\right)−\mathrm{5} \\ $$$$=>\boldsymbol{{f}}'\left(−\mathrm{2}\right)=−\mathrm{5}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)=\left(\mathrm{2}\right)=>−\mathrm{5}=\mathrm{2}\boldsymbol{{m}}+\mathrm{1}=>\boldsymbol{{m}}=−\mathrm{3}\:\bigstar{Moivre} \\ $$$$\begin{array}{|c|c|}{\boldsymbol{{m}}=−\mathrm{3}}\\{\boldsymbol{{f}}'\left(−\mathrm{2}\right)=−\mathrm{5}}\\\hline\end{array} \\ $$$$ \\ $$
Commented by 073 last updated on 03/Mar/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$
Answered by Frix last updated on 04/Mar/23
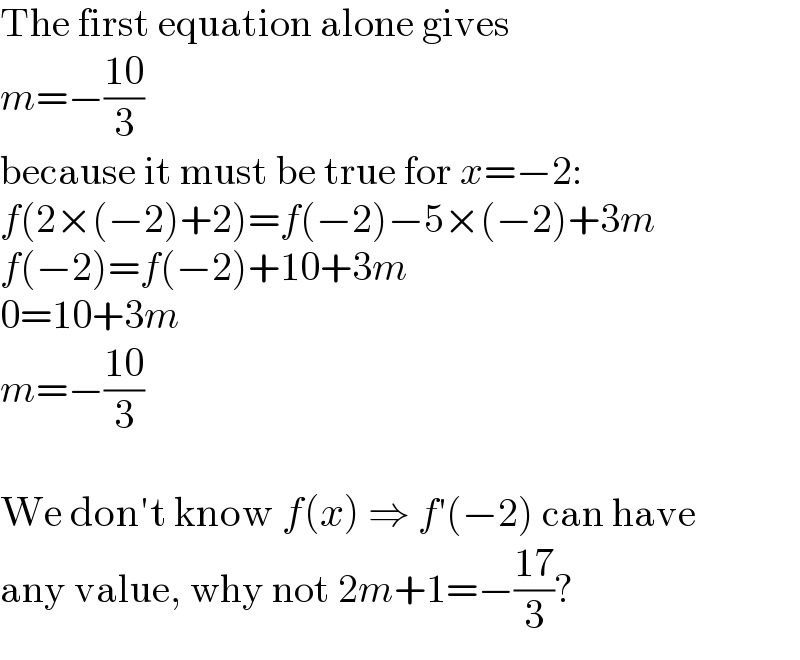
$$\mathrm{The}\:\mathrm{first}\:\mathrm{equation}\:\mathrm{alone}\:\mathrm{gives} \\ $$$${m}=−\frac{\mathrm{10}}{\mathrm{3}} \\ $$$$\mathrm{because}\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{true}\:\mathrm{for}\:{x}=−\mathrm{2}: \\ $$$${f}\left(\mathrm{2}×\left(−\mathrm{2}\right)+\mathrm{2}\right)={f}\left(−\mathrm{2}\right)−\mathrm{5}×\left(−\mathrm{2}\right)+\mathrm{3}{m} \\ $$$${f}\left(−\mathrm{2}\right)={f}\left(−\mathrm{2}\right)+\mathrm{10}+\mathrm{3}{m} \\ $$$$\mathrm{0}=\mathrm{10}+\mathrm{3}{m} \\ $$$${m}=−\frac{\mathrm{10}}{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:{f}\left({x}\right)\:\Rightarrow\:{f}'\left(−\mathrm{2}\right)\:\mathrm{can}\:\mathrm{have} \\ $$$$\mathrm{any}\:\mathrm{value},\:\mathrm{why}\:\mathrm{not}\:\mathrm{2}{m}+\mathrm{1}=−\frac{\mathrm{17}}{\mathrm{3}}? \\ $$
Commented by manxsol last updated on 05/Mar/23

$${Thanks},{Sir}\:{Frix} \\ $$
