
Question Number 188568 by 073 last updated on 03/Mar/23
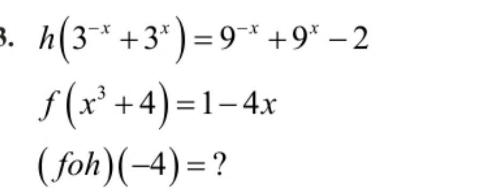
Answered by floor(10²Eta[1]) last updated on 03/Mar/23
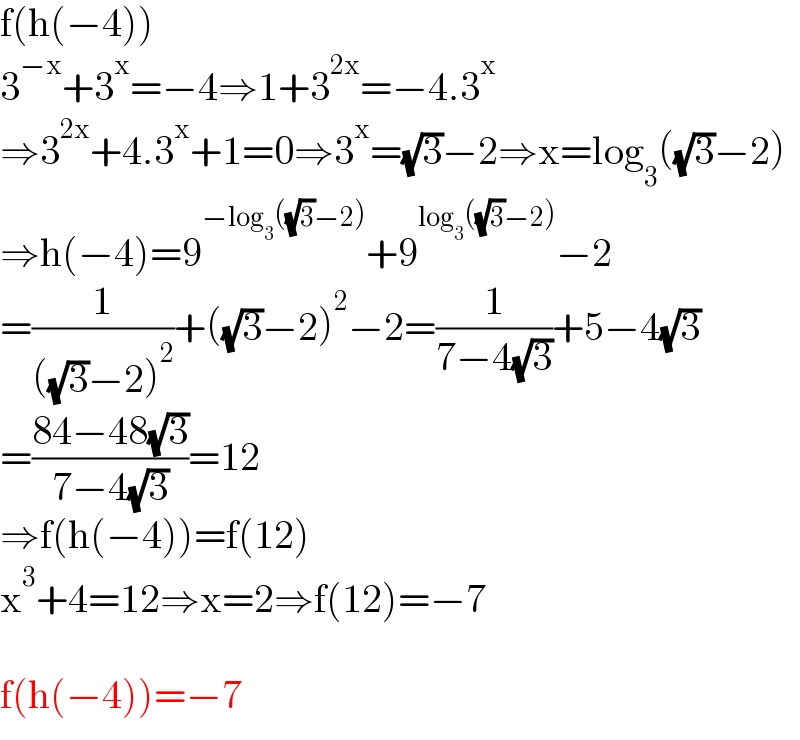
$$\mathrm{f}\left(\mathrm{h}\left(−\mathrm{4}\right)\right) \\ $$$$\mathrm{3}^{−\mathrm{x}} +\mathrm{3}^{\mathrm{x}} =−\mathrm{4}\Rightarrow\mathrm{1}+\mathrm{3}^{\mathrm{2x}} =−\mathrm{4}.\mathrm{3}^{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{2x}} +\mathrm{4}.\mathrm{3}^{\mathrm{x}} +\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{3}^{\mathrm{x}} =\sqrt{\mathrm{3}}−\mathrm{2}\Rightarrow\mathrm{x}=\mathrm{log}_{\mathrm{3}} \left(\sqrt{\mathrm{3}}−\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{h}\left(−\mathrm{4}\right)=\mathrm{9}^{−\mathrm{log}_{\mathrm{3}} \left(\sqrt{\mathrm{3}}−\mathrm{2}\right)} +\mathrm{9}^{\mathrm{log}_{\mathrm{3}} \left(\sqrt{\mathrm{3}}−\mathrm{2}\right)} −\mathrm{2} \\ $$$$=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{3}}−\mathrm{2}\right)^{\mathrm{2}} }+\left(\sqrt{\mathrm{3}}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}=\frac{\mathrm{1}}{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}}+\mathrm{5}−\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$=\frac{\mathrm{84}−\mathrm{48}\sqrt{\mathrm{3}}}{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}}=\mathrm{12} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{h}\left(−\mathrm{4}\right)\right)=\mathrm{f}\left(\mathrm{12}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{4}=\mathrm{12}\Rightarrow\mathrm{x}=\mathrm{2}\Rightarrow\mathrm{f}\left(\mathrm{12}\right)=−\mathrm{7} \\ $$$$ \\ $$$$\mathrm{f}\left(\mathrm{h}\left(−\mathrm{4}\right)\right)=−\mathrm{7} \\ $$
Commented by 073 last updated on 03/Mar/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$$$\mathrm{thanks} \\ $$
Answered by manxsol last updated on 04/Mar/23
![y=3^x +(1/3^x )⇒y^2 =9^x +(1/9^x )+2 h(y)=y^2 −4 h(x)=x^2 −4 foh ((ℜ),() ) h^( ↷) ((([-4,+∞^() ])),() ) f^↷ ((([-7,+∞])),() ) f(h(−4))= h(-4)=12 f(12)=f(x^3 +4)=1−4x 12=x^3 +4x⇒x=2 f(12)=1−4(2) f(12)=−7 f(h(−4))=−7](Q188666.png)
$${y}=\mathrm{3}^{{x}} +\frac{\mathrm{1}}{\mathrm{3}^{{x}} }\Rightarrow{y}^{\mathrm{2}} =\mathrm{9}^{{x}} +\frac{\mathrm{1}}{\mathrm{9}^{{x}} }+\mathrm{2} \\ $$$${h}\left({y}\right)={y}^{\mathrm{2}} −\mathrm{4} \\ $$$${h}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{4} \\ $$$${foh} \\ $$$$\begin{pmatrix}{\Re}\\{}\end{pmatrix}\:\overset{\:\:\curvearrowright} {{h}}\:\:\begin{pmatrix}{\left[-\mathrm{4},\overset{} {+\infty}\right]}\\{}\end{pmatrix}\:\:\overset{\curvearrowright} {{f}}\:\:\begin{pmatrix}{\left[-\mathrm{7},+\infty\right]}\\{}\end{pmatrix} \\ $$$${f}\left({h}\left(−\mathrm{4}\right)\right)= \\ $$$${h}\left(-\mathrm{4}\right)=\mathrm{12} \\ $$$${f}\left(\mathrm{12}\right)={f}\left({x}^{\mathrm{3}} +\mathrm{4}\right)=\mathrm{1}−\mathrm{4}{x} \\ $$$$\mathrm{12}={x}^{\mathrm{3}} +\mathrm{4}{x}\Rightarrow{x}=\mathrm{2} \\ $$$${f}\left(\mathrm{12}\right)=\mathrm{1}−\mathrm{4}\left(\mathrm{2}\right) \\ $$$${f}\left(\mathrm{12}\right)=−\mathrm{7} \\ $$$${f}\left({h}\left(−\mathrm{4}\right)\right)=−\mathrm{7} \\ $$
