
Question Number 188535 by Rupesh123 last updated on 03/Mar/23
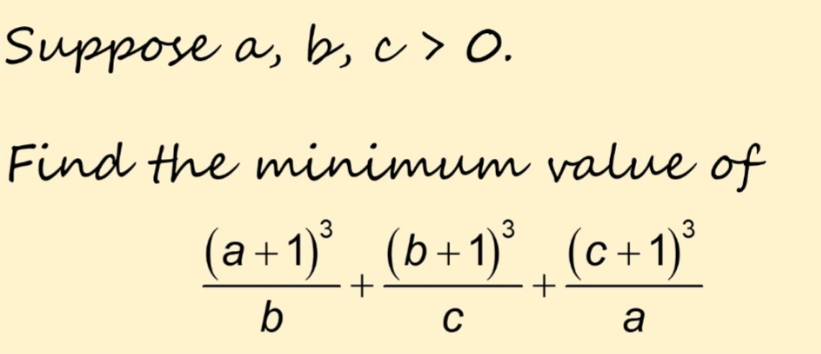
Answered by mr W last updated on 03/Mar/23
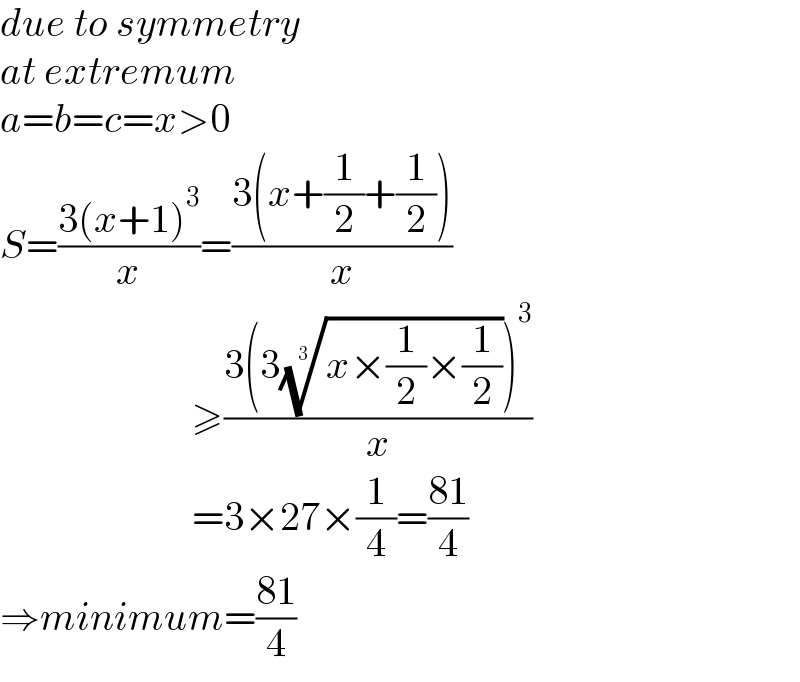
$${due}\:{to}\:{symmetry} \\ $$$${at}\:{extremum} \\ $$$${a}={b}={c}={x}>\mathrm{0} \\ $$$${S}=\frac{\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{{x}}=\frac{\mathrm{3}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\geqslant\frac{\mathrm{3}\left(\mathrm{3}\sqrt[{\mathrm{3}}]{{x}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}}\right)^{\mathrm{3}} }{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}×\mathrm{27}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{81}}{\mathrm{4}} \\ $$$$\Rightarrow{minimum}=\frac{\mathrm{81}}{\mathrm{4}} \\ $$
Commented by Rupesh123 last updated on 03/Mar/23
Excellent
Commented by cortano12 last updated on 04/Mar/23
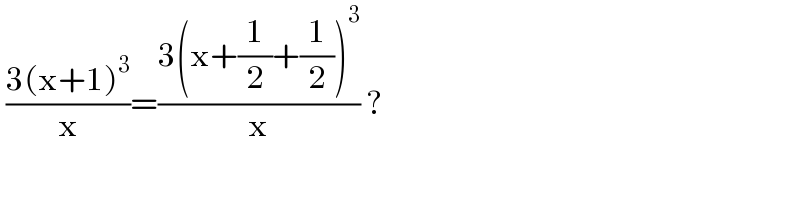
$$\:\frac{\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{x}}=\frac{\mathrm{3}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }{\mathrm{x}}\:? \\ $$
