Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 188417 by 073 last updated on 01/Mar/23

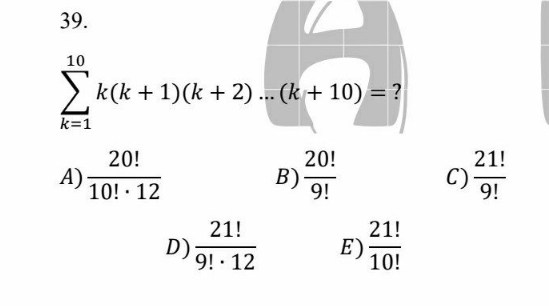
Commented by SEKRET last updated on 01/Mar/23

D

$$\:\boldsymbol{\mathrm{D}} \\ $$

Answered by SEKRET last updated on 01/Mar/23

Σ_(k=1) ^(10) (((k−1)!∙k∙(k+1)....(k+10))/((k−1)!))=? Σ_(k=1) ^(10) (((k+10)!)/((k−1)!))=Σ_(k=1) ^(10) (((k+10)!∙(k+11−(k−1)))/(12∙(k−1)!)) Σ_(k=1) ^(10) (((k+11)! −(k+10)!∙(k−1))/(12∙(k−1)!)) = =(1/(12))∙Σ_(k=1) ^(10) ((((k+11)!)/((k−1)!)) − (((k+10)!∙(k−1))/((k−1)!)))= = (1/(12))∙(((12!)/(0!))−((11!∙0)/(0!))+((13!)/(1!))−((12!)/(0!))+((14!)/(2!))−((13!)/(1!))+...+((21!)/(9!))−((20!)/(8!))) =(1/(12))∙(((12!)/(0!))+((13!)/(1!))−((12!)/(0!))+((14!)/(2!))−((13!)/(1!))+...+((21!)/(9!))−((20!)/(8!))) = ((21!)/(12∙9!)) ABDULAZIZ ABDUVALIYEV

$$\:\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\frac{\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!\centerdot\boldsymbol{\mathrm{k}}\centerdot\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)....\left(\boldsymbol{\mathrm{k}}+\mathrm{10}\right)}{\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!}=? \\ $$$$\:\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\:\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{10}\right)!}{\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!}=\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{10}\right)!\centerdot\left(\boldsymbol{\mathrm{k}}+\mathrm{11}−\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)\right)}{\mathrm{12}\centerdot\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!} \\ $$$$\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\:\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{11}\right)!\:−\left(\boldsymbol{\mathrm{k}}+\mathrm{10}\right)!\centerdot\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)}{\mathrm{12}\centerdot\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\centerdot\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\:\left(\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{11}\right)!}{\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!}\:−\:\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{10}\right)!\centerdot\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)}{\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)!}\right)= \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{12}}\centerdot\left(\frac{\mathrm{12}!}{\mathrm{0}!}−\frac{\mathrm{11}!\centerdot\mathrm{0}}{\mathrm{0}!}+\frac{\mathrm{13}!}{\mathrm{1}!}−\frac{\mathrm{12}!}{\mathrm{0}!}+\frac{\mathrm{14}!}{\mathrm{2}!}−\frac{\mathrm{13}!}{\mathrm{1}!}+...+\frac{\mathrm{21}!}{\mathrm{9}!}−\frac{\mathrm{20}!}{\mathrm{8}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\centerdot\left(\frac{\mathrm{12}!}{\mathrm{0}!}+\frac{\mathrm{13}!}{\mathrm{1}!}−\frac{\mathrm{12}!}{\mathrm{0}!}+\frac{\mathrm{14}!}{\mathrm{2}!}−\frac{\mathrm{13}!}{\mathrm{1}!}+...+\frac{\mathrm{21}!}{\mathrm{9}!}−\frac{\mathrm{20}!}{\mathrm{8}!}\right) \\ $$$$=\:\frac{\mathrm{21}!}{\mathrm{12}\centerdot\mathrm{9}!} \\ $$$$\:\:\boldsymbol{{ABDULAZIZ}}\:\:\:\boldsymbol{{ABDUVALIYEV}} \\ $$$$ \\ $$

Commented by 073 last updated on 02/Mar/23

nice solution

$$\mathrm{nice}\:\mathrm{solution} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com