
Question Number 188310 by normans last updated on 27/Feb/23
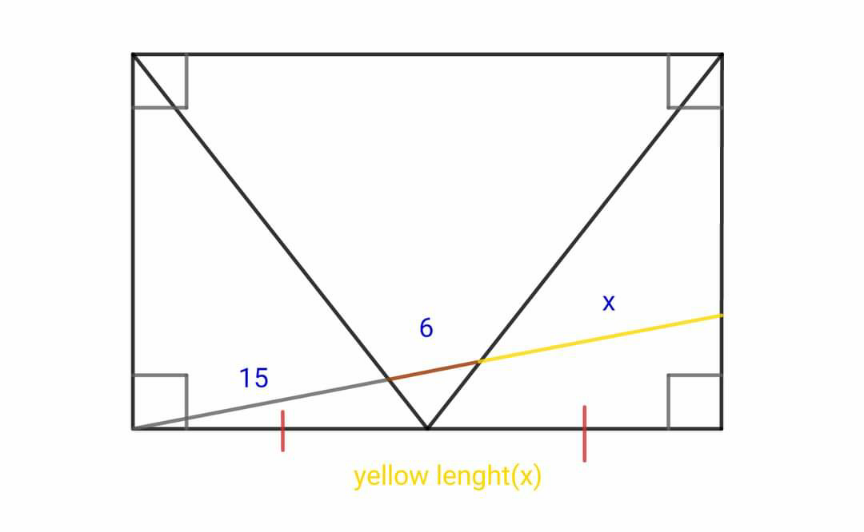
Commented by normans last updated on 27/Feb/23
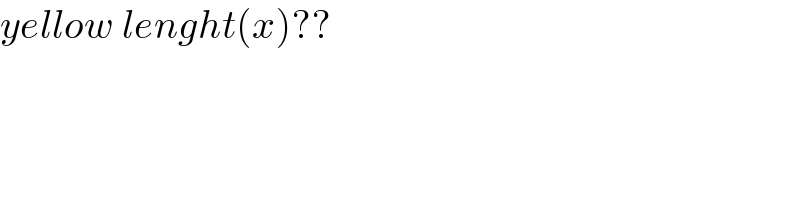
$${yellow}\:{lenght}\left({x}\right)?? \\ $$
Answered by HeferH last updated on 27/Feb/23

$$\mathrm{15} \\ $$
Answered by mr W last updated on 27/Feb/23
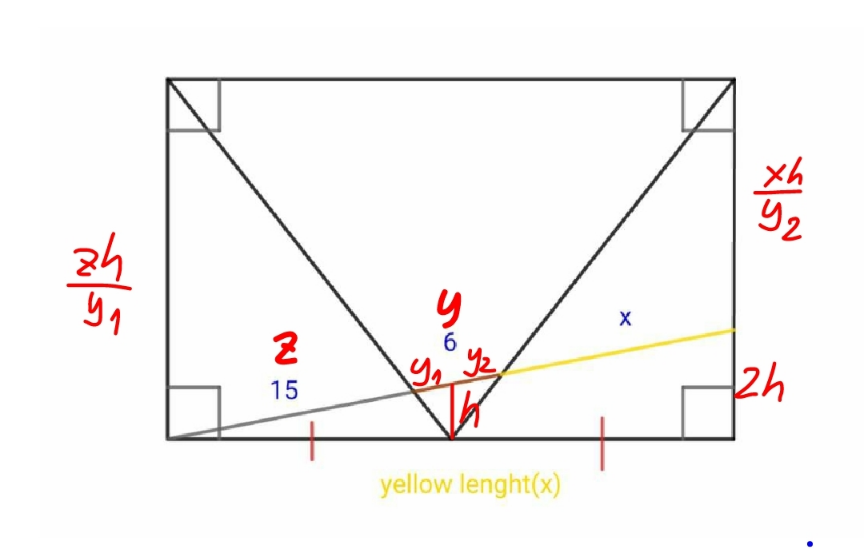
Commented by mr W last updated on 27/Feb/23
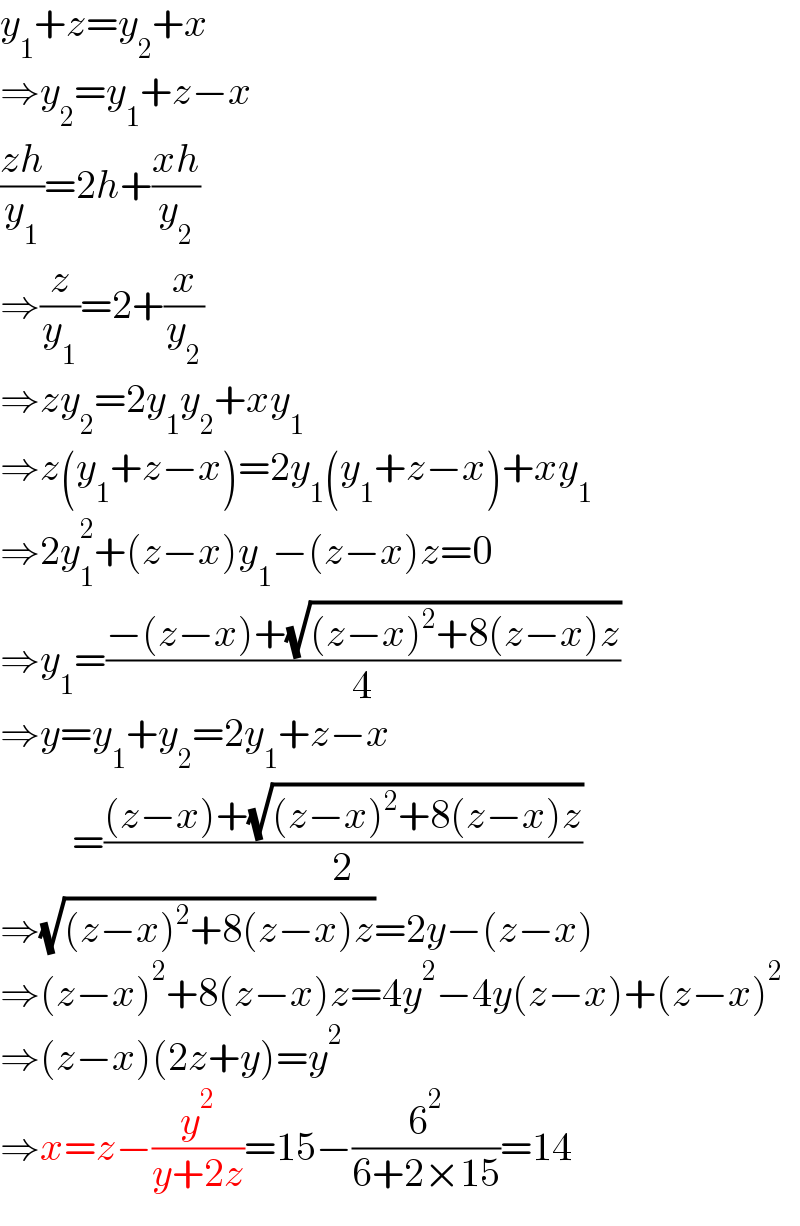
$${y}_{\mathrm{1}} +{z}={y}_{\mathrm{2}} +{x} \\ $$$$\Rightarrow{y}_{\mathrm{2}} ={y}_{\mathrm{1}} +{z}−{x} \\ $$$$\frac{{zh}}{{y}_{\mathrm{1}} }=\mathrm{2}{h}+\frac{{xh}}{{y}_{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{z}}{{y}_{\mathrm{1}} }=\mathrm{2}+\frac{{x}}{{y}_{\mathrm{2}} } \\ $$$$\Rightarrow{zy}_{\mathrm{2}} =\mathrm{2}{y}_{\mathrm{1}} {y}_{\mathrm{2}} +{xy}_{\mathrm{1}} \\ $$$$\Rightarrow{z}\left({y}_{\mathrm{1}} +{z}−{x}\right)=\mathrm{2}{y}_{\mathrm{1}} \left({y}_{\mathrm{1}} +{z}−{x}\right)+{xy}_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}{y}_{\mathrm{1}} ^{\mathrm{2}} +\left({z}−{x}\right){y}_{\mathrm{1}} −\left({z}−{x}\right){z}=\mathrm{0} \\ $$$$\Rightarrow{y}_{\mathrm{1}} =\frac{−\left({z}−{x}\right)+\sqrt{\left({z}−{x}\right)^{\mathrm{2}} +\mathrm{8}\left({z}−{x}\right){z}}}{\mathrm{4}} \\ $$$$\Rightarrow{y}={y}_{\mathrm{1}} +{y}_{\mathrm{2}} =\mathrm{2}{y}_{\mathrm{1}} +{z}−{x} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\left({z}−{x}\right)+\sqrt{\left({z}−{x}\right)^{\mathrm{2}} +\mathrm{8}\left({z}−{x}\right){z}}}{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\left({z}−{x}\right)^{\mathrm{2}} +\mathrm{8}\left({z}−{x}\right){z}}=\mathrm{2}{y}−\left({z}−{x}\right) \\ $$$$\Rightarrow\left({z}−{x}\right)^{\mathrm{2}} +\mathrm{8}\left({z}−{x}\right){z}=\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}{y}\left({z}−{x}\right)+\left({z}−{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left({z}−{x}\right)\left(\mathrm{2}{z}+{y}\right)={y}^{\mathrm{2}} \\ $$$$\Rightarrow{x}={z}−\frac{{y}^{\mathrm{2}} }{{y}+\mathrm{2}{z}}=\mathrm{15}−\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{6}+\mathrm{2}×\mathrm{15}}=\mathrm{14} \\ $$
