Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 188163 by normans last updated on 26/Feb/23

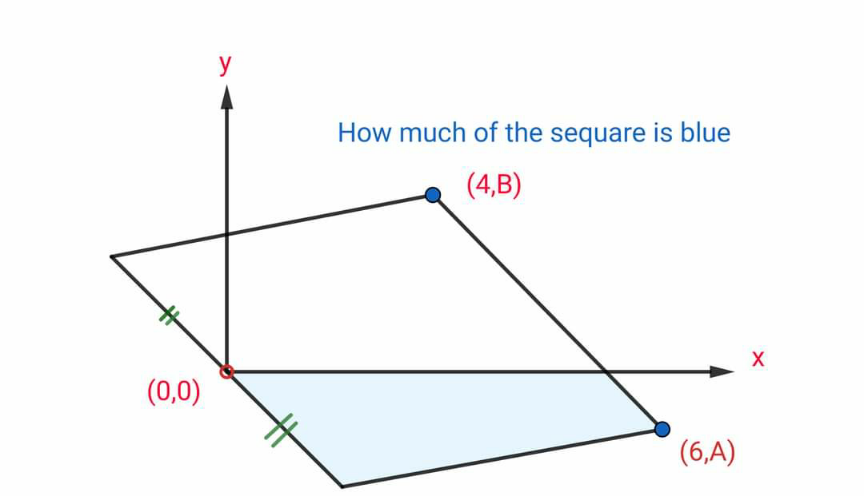
Commented by mr W last updated on 26/Feb/23

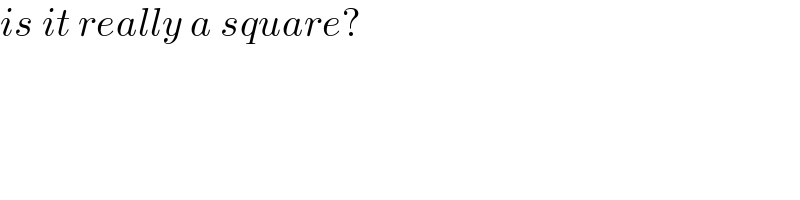
is it really a square?

$${is}\:{it}\:{really}\:{a}\:{square}? \\ $$

Commented by normans last updated on 26/Feb/23

yes

$${yes} \\ $$

Answered by mr W last updated on 26/Feb/23

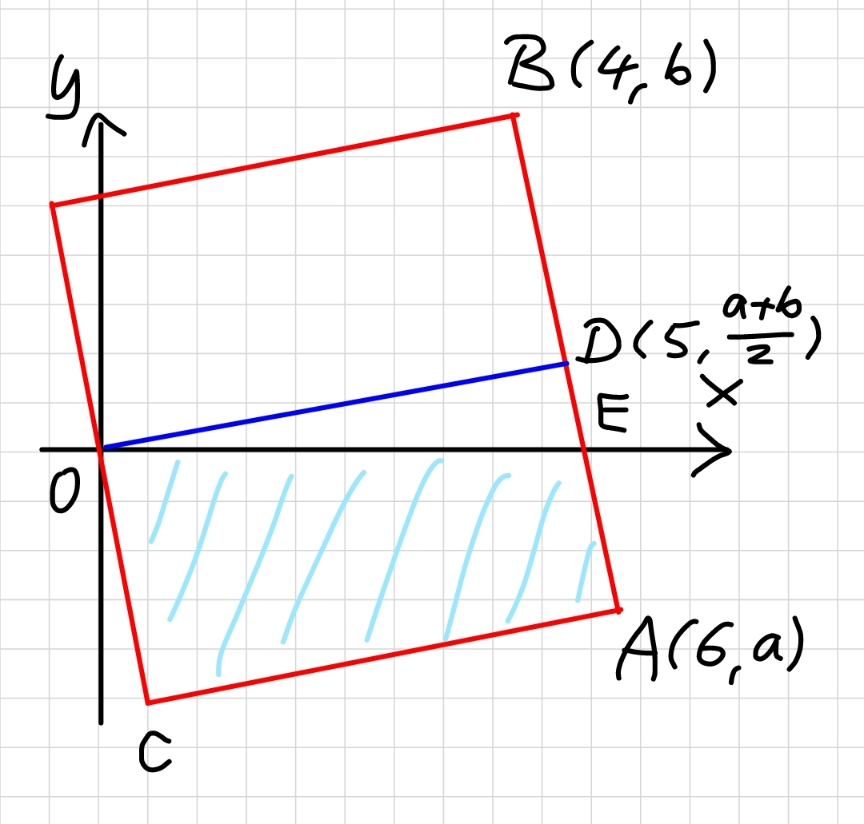
Commented by mr W last updated on 26/Feb/23

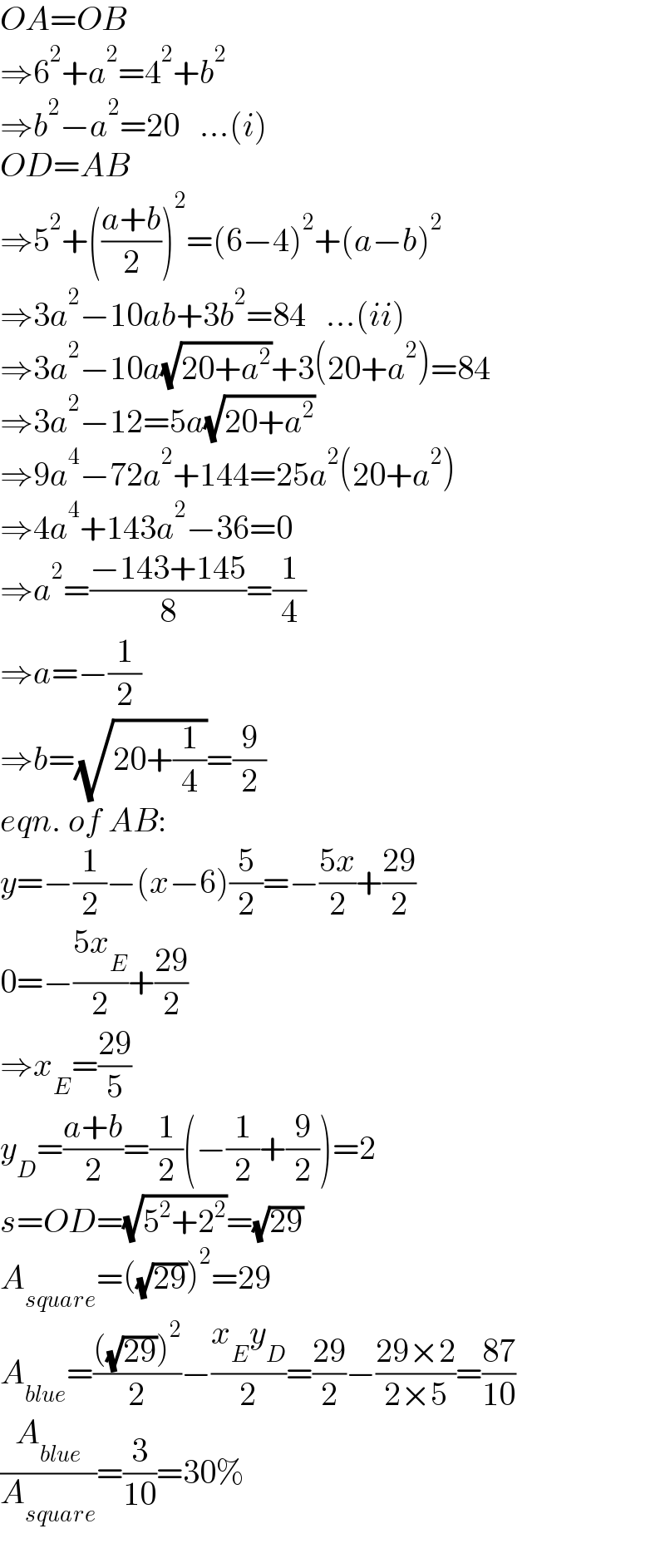
OA=OB ⇒6^2 +a^2 =4^2 +b^2 ⇒b^2 −a^2 =20 ...(i) OD=AB ⇒5^2 +(((a+b)/2))^2 =(6−4)^2 +(a−b)^2 ⇒3a^2 −10ab+3b^2 =84 ...(ii) ⇒3a^2 −10a(√(20+a^2 ))+3(20+a^2 )=84 ⇒3a^2 −12=5a(√(20+a^2 )) ⇒9a^4 −72a^2 +144=25a^2 (20+a^2 ) ⇒4a^4 +143a^2 −36=0 ⇒a^2 =((−143+145)/8)=(1/4) ⇒a=−(1/2) ⇒b=(√(20+(1/4)))=(9/2) eqn. of AB: y=−(1/2)−(x−6)(5/2)=−((5x)/2)+((29)/2) 0=−((5x_E )/2)+((29)/2) ⇒x_E =((29)/5) y_D =((a+b)/2)=(1/2)(−(1/2)+(9/2))=2 s=OD=(√(5^2 +2^2 ))=(√(29)) A_(square) =((√(29)))^2 =29 A_(blue) =((((√(29)))^2 )/2)−((x_E y_D )/2)=((29)/2)−((29×2)/(2×5))=((87)/(10)) (A_(blue) /A_(square) )=(3/(10))=30%

$${OA}={OB} \\ $$$$\Rightarrow\mathrm{6}^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{20}\:\:\:...\left({i}\right) \\ $$$${OD}={AB} \\ $$$$\Rightarrow\mathrm{5}^{\mathrm{2}} +\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\mathrm{6}−\mathrm{4}\right)^{\mathrm{2}} +\left({a}−{b}\right)^{\mathrm{2}} \: \\ $$$$\Rightarrow\mathrm{3}{a}^{\mathrm{2}} −\mathrm{10}{ab}+\mathrm{3}{b}^{\mathrm{2}} =\mathrm{84}\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow\mathrm{3}{a}^{\mathrm{2}} −\mathrm{10}{a}\sqrt{\mathrm{20}+{a}^{\mathrm{2}} }+\mathrm{3}\left(\mathrm{20}+{a}^{\mathrm{2}} \right)=\mathrm{84} \\ $$$$\Rightarrow\mathrm{3}{a}^{\mathrm{2}} −\mathrm{12}=\mathrm{5}{a}\sqrt{\mathrm{20}+{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{9}{a}^{\mathrm{4}} −\mathrm{72}{a}^{\mathrm{2}} +\mathrm{144}=\mathrm{25}{a}^{\mathrm{2}} \left(\mathrm{20}+{a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{4}{a}^{\mathrm{4}} +\mathrm{143}{a}^{\mathrm{2}} −\mathrm{36}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{−\mathrm{143}+\mathrm{145}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{a}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{b}=\sqrt{\mathrm{20}+\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$${y}=−\frac{\mathrm{1}}{\mathrm{2}}−\left({x}−\mathrm{6}\right)\frac{\mathrm{5}}{\mathrm{2}}=−\frac{\mathrm{5}{x}}{\mathrm{2}}+\frac{\mathrm{29}}{\mathrm{2}} \\ $$$$\mathrm{0}=−\frac{\mathrm{5}{x}_{{E}} }{\mathrm{2}}+\frac{\mathrm{29}}{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{E}} =\frac{\mathrm{29}}{\mathrm{5}} \\ $$$${y}_{{D}} =\frac{{a}+{b}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{2}}\right)=\mathrm{2} \\ $$$${s}={OD}=\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }=\sqrt{\mathrm{29}} \\ $$$${A}_{{square}} =\left(\sqrt{\mathrm{29}}\right)^{\mathrm{2}} =\mathrm{29} \\ $$$${A}_{{blue}} =\frac{\left(\sqrt{\mathrm{29}}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}_{{E}} {y}_{{D}} }{\mathrm{2}}=\frac{\mathrm{29}}{\mathrm{2}}−\frac{\mathrm{29}×\mathrm{2}}{\mathrm{2}×\mathrm{5}}=\frac{\mathrm{87}}{\mathrm{10}} \\ $$$$\frac{{A}_{{blue}} }{{A}_{{square}} }=\frac{\mathrm{3}}{\mathrm{10}}=\mathrm{30\%} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com