Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 188147 by normans last updated on 26/Feb/23

Answered by Rasheed.Sindhi last updated on 26/Feb/23

5 ∣ ABC ⇒C=0 or 5 C=0⇒D=0,4,8 [∵ 4∣ABCD] C=5⇒D=2,6 [∵ 4∣ABCD] CD=00,04,08,52,56 BCD=000,900,504,108,252,756 [∵9∣BCD] B=0⇒A=3,6,9 [∵ 6∣AB ] B=9,5,1,7⇒A has no value [∵ 6∣AB ] B=2⇒A=1,4,7 [∵ 6∣AB ] A=1,3,4,6,7,9

$$\mathrm{5}\:\mid\:{ABC}\:\Rightarrow{C}=\mathrm{0}\:{or}\:\mathrm{5} \\ $$$${C}=\mathrm{0}\Rightarrow{D}=\mathrm{0},\mathrm{4},\mathrm{8}\:\:\left[\because\:\mathrm{4}\mid{ABCD}\right] \\ $$$${C}=\mathrm{5}\Rightarrow{D}=\mathrm{2},\mathrm{6}\:\:\:\:\:\:\left[\because\:\mathrm{4}\mid{ABCD}\right] \\ $$$${CD}=\mathrm{00},\mathrm{04},\mathrm{08},\mathrm{52},\mathrm{56} \\ $$$${BCD}=\mathrm{000},\mathrm{900},\mathrm{504},\mathrm{108},\mathrm{252},\mathrm{756}\:\:\left[\because\mathrm{9}\mid{BCD}\right] \\ $$$${B}=\mathrm{0}\Rightarrow{A}=\mathrm{3},\mathrm{6},\mathrm{9}\:\:\:\:\left[\because\:\mathrm{6}\mid{AB}\:\right] \\ $$$${B}=\mathrm{9},\mathrm{5},\mathrm{1},\mathrm{7}\Rightarrow{A}\:{has}\:{no}\:{value}\:\left[\because\:\mathrm{6}\mid{AB}\:\right] \\ $$$${B}=\mathrm{2}\Rightarrow{A}=\mathrm{1},\mathrm{4},\mathrm{7}\:\:\:\:\:\:\left[\because\:\mathrm{6}\mid{AB}\:\right] \\ $$$$ \\ $$$${A}=\mathrm{1},\mathrm{3},\mathrm{4},\mathrm{6},\mathrm{7},\mathrm{9} \\ $$

Commented by JDamian last updated on 26/Feb/23

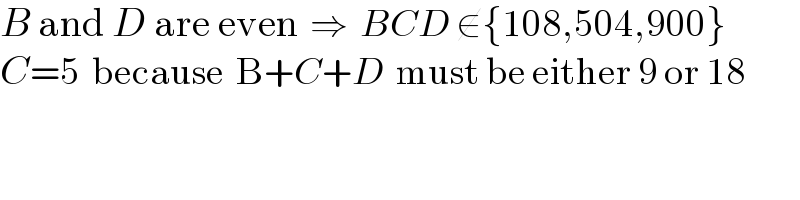
B and D are even ⇒ BCD ∉{108,504,900} C=5 because B+C+D must be either 9 or 18

$${B}\:\mathrm{and}\:{D}\:\mathrm{are}\:\mathrm{even}\:\:\Rightarrow\:\:{BCD}\:\notin\left\{\mathrm{108},\mathrm{504},\mathrm{900}\right\} \\ $$$${C}=\mathrm{5}\:\:\mathrm{because}\:\:\mathrm{B}+{C}+{D}\:\:\mathrm{must}\:\mathrm{be}\:\mathrm{either}\:\mathrm{9}\:\mathrm{or}\:\mathrm{18} \\ $$

Commented by Rasheed.Sindhi last updated on 26/Feb/23

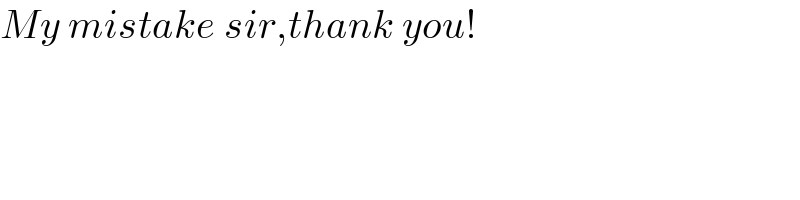
My mistake sir,thank you!

$${My}\:{mistake}\:{sir},{thank}\:{you}! \\ $$

Answered by mr W last updated on 26/Feb/23

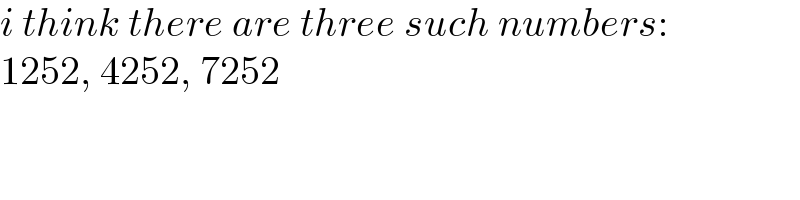
i think there are three such numbers: 1252, 4252, 7252

$${i}\:{think}\:{there}\:{are}\:{three}\:{such}\:{numbers}: \\ $$$$\mathrm{1252},\:\mathrm{4252},\:\mathrm{7252} \\ $$

Commented by mr W last updated on 26/Feb/23

ABCD B=even, ≤8 C=0 or 5 B+C+D=9 or 18 if C=0: B+D=9 ⇒D=odd ⇒rejected B+D=18 ⇒D≥10 ⇒impossible if C=5: B+D=4 ⇒(B, D)=(0,4) or (4,0) or (2,2) B+D=13 ⇒D=odd ⇒rejected A054, A450, A252 are remaining. A054: A=6 or 9 ⇒not divisible by 4 ⇒rejected A450: A=2 or 5 or 8 ⇒not divisible by 4 ⇒rejected A252: A=1 or 4 or 7 ⇒divisible by 4 ⇒ok so the number is 1252, 4252 or 7252.

$${ABCD} \\ $$$${B}={even},\:\leqslant\mathrm{8} \\ $$$${C}=\mathrm{0}\:{or}\:\mathrm{5} \\ $$$${B}+{C}+{D}=\mathrm{9}\:{or}\:\mathrm{18} \\ $$$${if}\:{C}=\mathrm{0}:\:{B}+{D}=\mathrm{9}\:\Rightarrow{D}={odd}\:\Rightarrow{rejected} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{B}+{D}=\mathrm{18}\:\Rightarrow{D}\geqslant\mathrm{10}\:\Rightarrow{impossible} \\ $$$${if}\:{C}=\mathrm{5}:\:{B}+{D}=\mathrm{4}\:\Rightarrow\left({B},\:{D}\right)=\left(\mathrm{0},\mathrm{4}\right)\:{or}\:\left(\mathrm{4},\mathrm{0}\right)\:{or}\:\left(\mathrm{2},\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{B}+{D}=\mathrm{13}\:\Rightarrow{D}={odd}\:\Rightarrow{rejected} \\ $$$${A}\mathrm{054},\:{A}\mathrm{450},\:{A}\mathrm{252}\:{are}\:{remaining}. \\ $$$${A}\mathrm{054}:\:{A}=\mathrm{6}\:{or}\:\mathrm{9}\:\Rightarrow{not}\:{divisible}\:{by}\:\mathrm{4}\:\Rightarrow{rejected} \\ $$$${A}\mathrm{450}:\:{A}=\mathrm{2}\:{or}\:\mathrm{5}\:{or}\:\mathrm{8}\:\Rightarrow{not}\:{divisible}\:{by}\:\mathrm{4}\:\Rightarrow{rejected} \\ $$$${A}\mathrm{252}:\:{A}=\mathrm{1}\:{or}\:\mathrm{4}\:{or}\:\mathrm{7}\:\Rightarrow{divisible}\:{by}\:\mathrm{4}\:\Rightarrow{ok} \\ $$$${so}\:{the}\:{number}\:{is}\:\mathrm{1252},\:\mathrm{4252}\:{or}\:\mathrm{7252}. \\ $$

Answered by manxsol last updated on 26/Feb/23

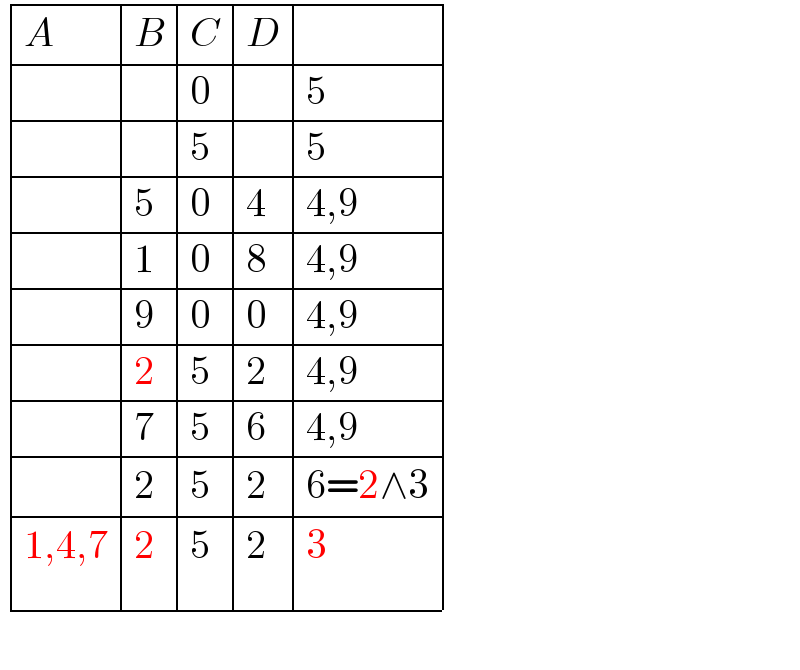
determinant ((A,B,C,D,),(,,0,,5),(,,5,,5),(,5,0,4,(4,9)),(,1,0,8,(4,9)),(,9,0,0,(4,9)),(,2,5,2,(4,9)),(,7,5,6,(4,9)),(,2,5,2,(6=2∧3)),((1,4,7),2,5,2,3))

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}{{A}}&\hline{{B}}&\hline{{C}}&\hline{{D}}&\hline{}\\{}&\hline{}&\hline{\mathrm{0}}&\hline{}&\hline{\mathrm{5}}\\{}&\hline{}&\hline{\mathrm{5}}&\hline{}&\hline{\mathrm{5}}\\{}&\hline{\mathrm{5}}&\hline{\mathrm{0}}&\hline{\mathrm{4}}&\hline{\mathrm{4},\mathrm{9}}\\{}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{8}}&\hline{\mathrm{4},\mathrm{9}}\\{}&\hline{\mathrm{9}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{4},\mathrm{9}}\\{}&\hline{\mathrm{2}}&\hline{\mathrm{5}}&\hline{\mathrm{2}}&\hline{\mathrm{4},\mathrm{9}}\\{}&\hline{\mathrm{7}}&\hline{\mathrm{5}}&\hline{\mathrm{6}}&\hline{\mathrm{4},\mathrm{9}}\\{}&\hline{\mathrm{2}}&\hline{\mathrm{5}}&\hline{\mathrm{2}}&\hline{\mathrm{6}=\mathrm{2}\wedge\mathrm{3}}\\{\mathrm{1},\mathrm{4},\mathrm{7}}&\hline{\mathrm{2}}&\hline{\mathrm{5}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}\\\hline\end{array} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com