
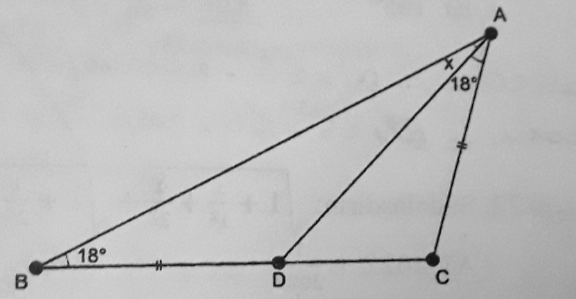
Question Number 188100 by Shrinava last updated on 25/Feb/23
Answered by a.lgnaoui last updated on 25/Feb/23
![△ADC ∡CDA=x+18; AC=b CD= ((sin 18)/b)=((sin (x+18))/a) ⇒(a/b)=((sin (x+18))/(sin 18)) (1) △ABC BD=AC=a BC=a+b ((sin(x+18) )/(a+b))=((sin 18)/a) a[sin (x+18)−sin 18]=bsin 18 (a/b)=((sin 18)/(sin (x+18)−sin 18)) (2) (1)=(2)⇒ ((sin (x+18))/(sin 18)) =((sin 18)/(sin (x+18)−sin 18)) posons z=sin (x+18) sin 18=c (z/c) =(c/(z−c))⇒ [z^2 −cz−c^2 =0] △=c^2 +4c { ((z=((c±(√(c^2 +4c^2 )))/2)=((c(1+(√5) ))/2))),(( 0< z<+1)) :} Aplication numerique: c=sin 18=0,309016994 z=(1/2)⇒ sin (x+18)=sin (30) x+18=30 [x=12]](Q188108.png)
$$\bigtriangleup{ADC}\:\:\:\:\measuredangle{CDA}={x}+\mathrm{18};\:\:{AC}={b}\:{CD}= \\ $$$$\frac{\mathrm{sin}\:\mathrm{18}}{{b}}=\frac{\mathrm{sin}\:\left({x}+\mathrm{18}\right)}{{a}}\:\Rightarrow\frac{\boldsymbol{{a}}}{\boldsymbol{{b}}}=\frac{\mathrm{sin}\:\:\left(\boldsymbol{{x}}+\mathrm{18}\right)}{\mathrm{sin}\:\mathrm{18}}\:\left(\mathrm{1}\right)\: \\ $$$$\bigtriangleup{ABC}\:\:{BD}={AC}={a}\:\:{BC}={a}+{b} \\ $$$$\:\:\:\:\frac{\mathrm{sin}\left({x}+\mathrm{18}\right)\:}{{a}+{b}}=\frac{\mathrm{sin}\:\mathrm{18}}{{a}} \\ $$$${a}\left[\mathrm{sin}\:\left({x}+\mathrm{18}\right)−\mathrm{sin}\:\mathrm{18}\right]={b}\mathrm{sin}\:\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{{a}}}{\boldsymbol{{b}}}=\frac{\mathrm{sin}\:\mathrm{18}}{\mathrm{sin}\:\left({x}+\mathrm{18}\right)−\mathrm{sin}\:\mathrm{18}}\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)=\left(\mathrm{2}\right)\Rightarrow\:\: \\ $$$$\:\frac{\mathrm{sin}\:\left({x}+\mathrm{18}\right)}{\mathrm{sin}\:\mathrm{18}}\:\:=\frac{\mathrm{sin}\:\mathrm{18}}{\mathrm{sin}\:\left({x}+\mathrm{18}\right)−\mathrm{sin}\:\mathrm{18}} \\ $$$${posons}\:\:\boldsymbol{{z}}=\mathrm{sin}\:\left(\boldsymbol{{x}}+\mathrm{18}\right)\:\:\:\:\mathrm{sin}\:\mathrm{18}=\boldsymbol{{c}} \\ $$$$\:\:\:\frac{\boldsymbol{{z}}}{\boldsymbol{{c}}}\:\:=\frac{\boldsymbol{{c}}}{\boldsymbol{{z}}−\boldsymbol{{c}}}\Rightarrow\:\left[\boldsymbol{{z}}^{\mathrm{2}} −\boldsymbol{{cz}}−\boldsymbol{{c}}^{\mathrm{2}} =\mathrm{0}\right] \\ $$$$\:\:\bigtriangleup={c}^{\mathrm{2}} +\mathrm{4}{c}\:\:\:\begin{cases}{\boldsymbol{{z}}=\frac{\boldsymbol{{c}}\pm\sqrt{{c}^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} }}{\mathrm{2}}=\frac{{c}\left(\mathrm{1}+\sqrt{\mathrm{5}}\:\right)}{\mathrm{2}}}\\{\:\mathrm{0}<\:\boldsymbol{{z}}<+\mathrm{1}}\end{cases} \\ $$$$\boldsymbol{{A}}{plication}\:{numerique}: \\ $$$$\:\:\:\:\:\:\:{c}=\mathrm{sin}\:\mathrm{18}=\mathrm{0},\mathrm{309016994} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{z}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\:\:\:\mathrm{sin}\:\left({x}+\mathrm{18}\right)=\mathrm{sin}\:\left(\mathrm{30}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}+\mathrm{18}=\mathrm{30} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\boldsymbol{{x}}=\mathrm{12}\right]\:\:\:\:\:\:\: \\ $$
Commented by a.lgnaoui last updated on 25/Feb/23

Commented by Shrinava last updated on 25/Feb/23
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by a.lgnaoui last updated on 26/Feb/23
$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by infinityaction last updated on 26/Feb/23

