Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 188079 by 073 last updated on 25/Feb/23

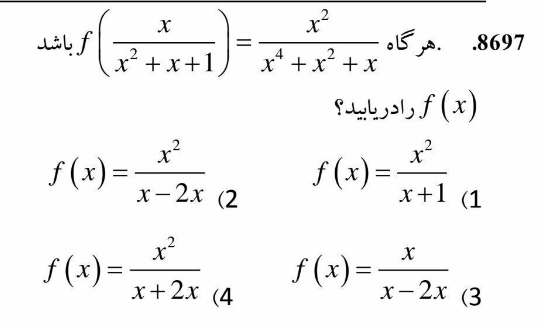
Commented by 073 last updated on 25/Feb/23

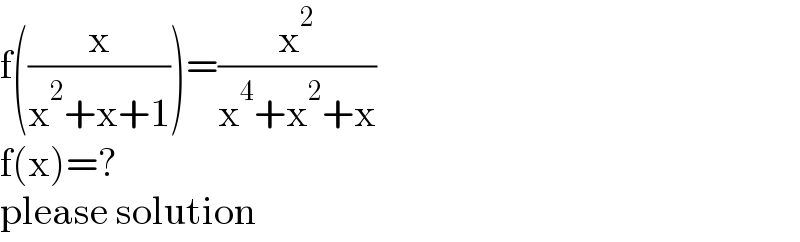
f((x/(x^2 +x+1)))=(x^2 /(x^4 +x^2 +x)) f(x)=? please solution

$$\mathrm{f}\left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{x}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=? \\ $$$$\mathrm{please}\:\mathrm{solution} \\ $$

Commented by mnjuly1970 last updated on 25/Feb/23

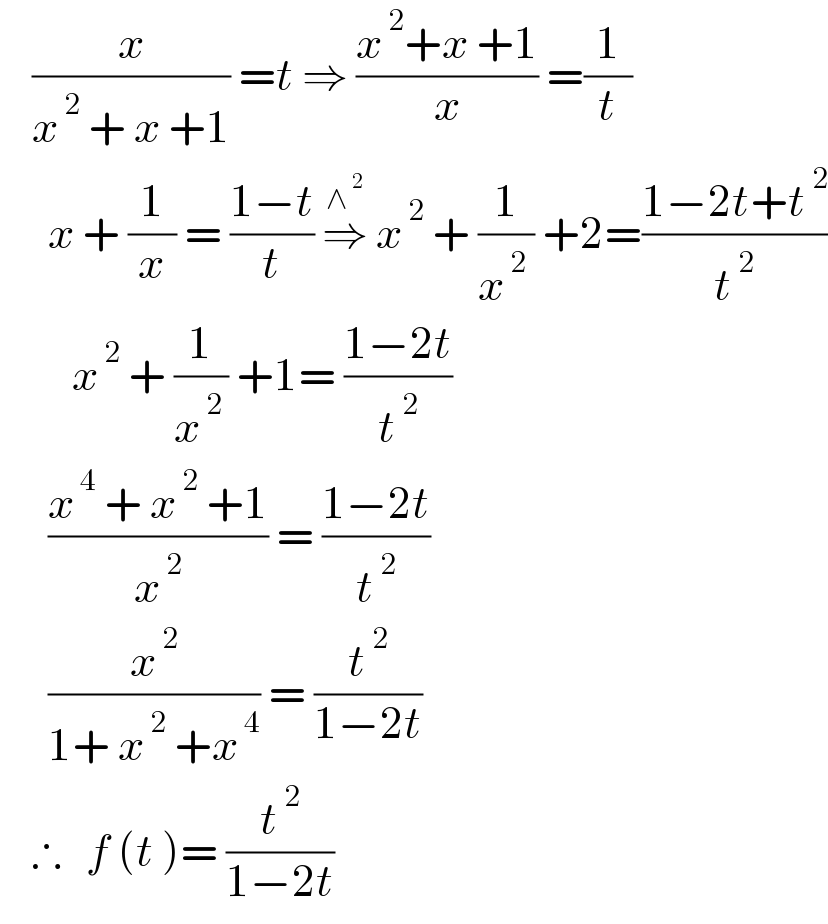
(x/(x^( 2) + x +1)) =t ⇒ ((x^( 2) +x +1)/x) =(1/t) x + (1/x) = ((1−t)/t) ⇒^∧^( 2) x^( 2) + (1/(x^( 2) )) +2=((1−2t+t^( 2) )/t^( 2) ) x^( 2) + (1/x^( 2 ) ) +1= ((1−2t)/t^( 2) ) ((x^( 4) + x^( 2) +1)/x^( 2) ) = ((1−2t)/t^( 2) ) (x^( 2) /(1+ x^( 2) +x^( 4) )) = (t^( 2) /(1−2t)) ∴ f (t )= (t^( 2) /(1−2t))

$$\:\:\:\:\frac{{x}}{{x}^{\:\mathrm{2}} \:+\:{x}\:+\mathrm{1}}\:={t}\:\Rightarrow\:\frac{{x}^{\:\mathrm{2}} +{x}\:+\mathrm{1}}{{x}}\:=\frac{\mathrm{1}}{{t}} \\ $$$$\:\:\:\:\:\:{x}\:+\:\frac{\mathrm{1}}{{x}}\:=\:\frac{\mathrm{1}−{t}}{{t}}\:\overset{\wedge^{\:\mathrm{2}} } {\Rightarrow}\:{x}^{\:\mathrm{2}} \:+\:\frac{\mathrm{1}}{{x}^{\:\mathrm{2}} \:}\:+\mathrm{2}=\frac{\mathrm{1}−\mathrm{2}{t}+{t}^{\:\mathrm{2}} }{{t}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:{x}^{\:\mathrm{2}} \:+\:\frac{\mathrm{1}}{{x}^{\:\mathrm{2}\:} }\:+\mathrm{1}=\:\frac{\mathrm{1}−\mathrm{2}{t}}{{t}^{\:\mathrm{2}} }\: \\ $$$$\:\:\:\:\:\:\frac{{x}^{\:\mathrm{4}} \:+\:{x}^{\:\mathrm{2}} \:+\mathrm{1}}{{x}^{\:\mathrm{2}} }\:=\:\frac{\mathrm{1}−\mathrm{2}{t}}{{t}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\frac{{x}^{\:\mathrm{2}} }{\mathrm{1}+\:{x}^{\:\mathrm{2}} \:+{x}^{\:\mathrm{4}} }\:=\:\frac{{t}^{\:\mathrm{2}} }{\mathrm{1}−\mathrm{2}{t}} \\ $$$$\:\:\:\:\therefore\:\:\:{f}\:\left({t}\:\right)=\:\frac{{t}^{\:\mathrm{2}} }{\mathrm{1}−\mathrm{2}{t}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com