
Question Number 188078 by Rupesh123 last updated on 25/Feb/23
Answered by a.lgnaoui last updated on 25/Feb/23
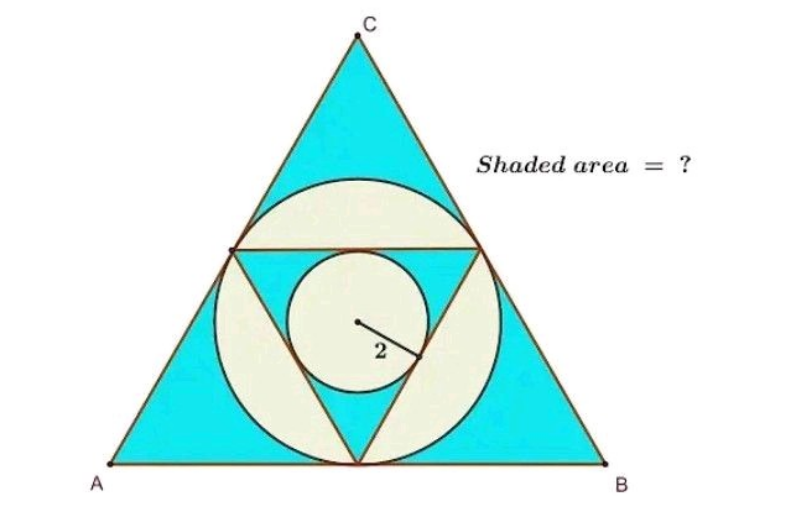
![from Graphe:△ABC Equilaterale big circle(radius OF=(√(4+((EF^2 )/4) )) ) sin (π/6)=(1/2)=(2/(OF))⇒(OF=4;EF=4(√(3.)) ) Area(big circleC_B =16π) Length of △ABC=8(√3) ⇒A=96(√3) Area(A_1 +A_2 +A_3 )=96(√3) −16π Area(C_B −C_S );C_S =Smal circle= 16π−4π=12π A′_1 +A_2 +A′_3 =[Area(smal triagle)−4π] =4(√3) ×(4(√3)×((√3)/2))−4π=24(√3) −4π Total Area=(A_1 +A_2 +A_3 )+(A_1 ′+A_2 ′+A_3 ′) (96(√3) −16π)+(24(√3) −4π)=120(√3) −20π ShadedArea=145](Q188085.png)
$${from}\:{Graphe}:\bigtriangleup{ABC}\:\:{Equilaterale} \\ $$$${big}\:{circle}\left({radius}\:{OF}=\sqrt{\mathrm{4}+\frac{{EF}^{\mathrm{2}} }{\mathrm{4}}\:}\:\right) \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}}{{OF}}\Rightarrow\left({OF}=\mathrm{4};{EF}=\mathrm{4}\sqrt{\mathrm{3}.}\:\:\right) \\ $$$${Area}\left({big}\:{circleC}_{{B}} =\mathrm{16}\pi\right) \\ $$$${Length}\:{of}\:\bigtriangleup{ABC}=\mathrm{8}\sqrt{\mathrm{3}}\:\:\Rightarrow{A}=\mathrm{96}\sqrt{\mathrm{3}} \\ $$$${Area}\left({A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} \right)=\mathrm{96}\sqrt{\mathrm{3}}\:−\mathrm{16}\pi \\ $$$${Area}\left({C}_{{B}} −{C}_{{S}} \right);{C}_{{S}} ={Smal}\:{circle}= \\ $$$$\mathrm{16}\pi−\mathrm{4}\pi=\mathrm{12}\pi \\ $$$${A}'_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}'_{\mathrm{3}} =\left[{Area}\left({smal}\:{triagle}\right)−\mathrm{4}\pi\right] \\ $$$$=\mathrm{4}\sqrt{\mathrm{3}}\:×\left(\mathrm{4}\sqrt{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−\mathrm{4}\pi=\mathrm{24}\sqrt{\mathrm{3}}\:−\mathrm{4}\pi \\ $$$${Total}\:{Area}=\left({A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} \right)+\left({A}_{\mathrm{1}} '+{A}_{\mathrm{2}} '+{A}_{\mathrm{3}} '\right) \\ $$$$\left(\mathrm{96}\sqrt{\mathrm{3}}\:−\mathrm{16}\pi\right)+\left(\mathrm{24}\sqrt{\mathrm{3}}\:−\mathrm{4}\pi\right)=\mathrm{120}\sqrt{\mathrm{3}}\:−\mathrm{20}\pi \\ $$$$ \\ $$$$\:\:\:\boldsymbol{{ShadedArea}}=\mathrm{145} \\ $$$$ \\ $$
Commented by Rupesh123 last updated on 25/Feb/23
Please check your solution well!
Commented by a.lgnaoui last updated on 25/Feb/23

$${thank}\:{you}. \\ $$
Commented by mr W last updated on 25/Feb/23

$${clearly}\:{wrong}! \\ $$$${the}\:{shaded}\:{area}\:{can}\:{not}\:{be}\:{more}\:{than} \\ $$$${the}\:{big}\:{equilateral}\:{triangle}! \\ $$
Commented by a.lgnaoui last updated on 25/Feb/23
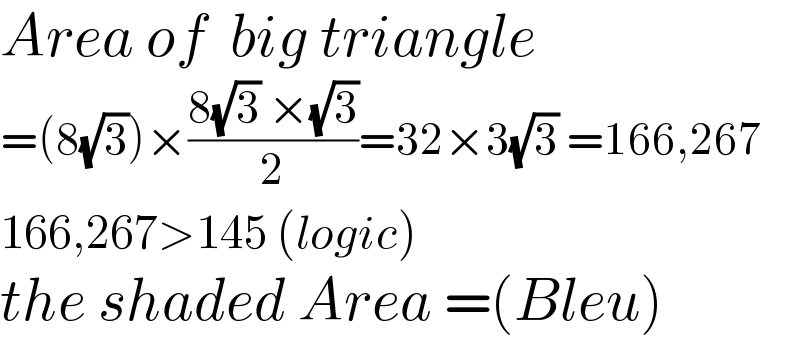
$${Area}\:{of}\:\:{big}\:{triangle}\: \\ $$$$=\left(\mathrm{8}\sqrt{\mathrm{3}}\right)×\frac{\mathrm{8}\sqrt{\mathrm{3}}\:×\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{32}×\mathrm{3}\sqrt{\mathrm{3}}\:=\mathrm{166},\mathrm{267} \\ $$$$\mathrm{166},\mathrm{267}>\mathrm{145}\:\left({logic}\right) \\ $$$${the}\:{shaded}\:{Area}\:=\left({Bleu}\right) \\ $$
Commented by mr W last updated on 25/Feb/23

$${you}\:{have}\:{paper}\:{and}\:{ruler},\:{why}\:{not} \\ $$$${draw}\:{such}\:{an}\:{equilateral}\:{and}\:{measure} \\ $$$${its}\:{base}\:{and}\:{height}\:{and}\:{then}\:{calculate} \\ $$$${its}\:{area}?\:{you}'{ll}\:{see}\:{its}\:{area}\:{is}\:{about} \\ $$$$\mathrm{83}.\:{when}\:{it}\:{is}\:{logic}\:{for}\:{you}\:{that}\:{the}\: \\ $$$${shaded}\:{area}\:{is}\:\mathrm{145},\:{then}\:{i}\:{must}\:{say} \\ $$$${you}\:{have}\:{no}\:{logic}. \\ $$
Answered by mr W last updated on 25/Feb/23
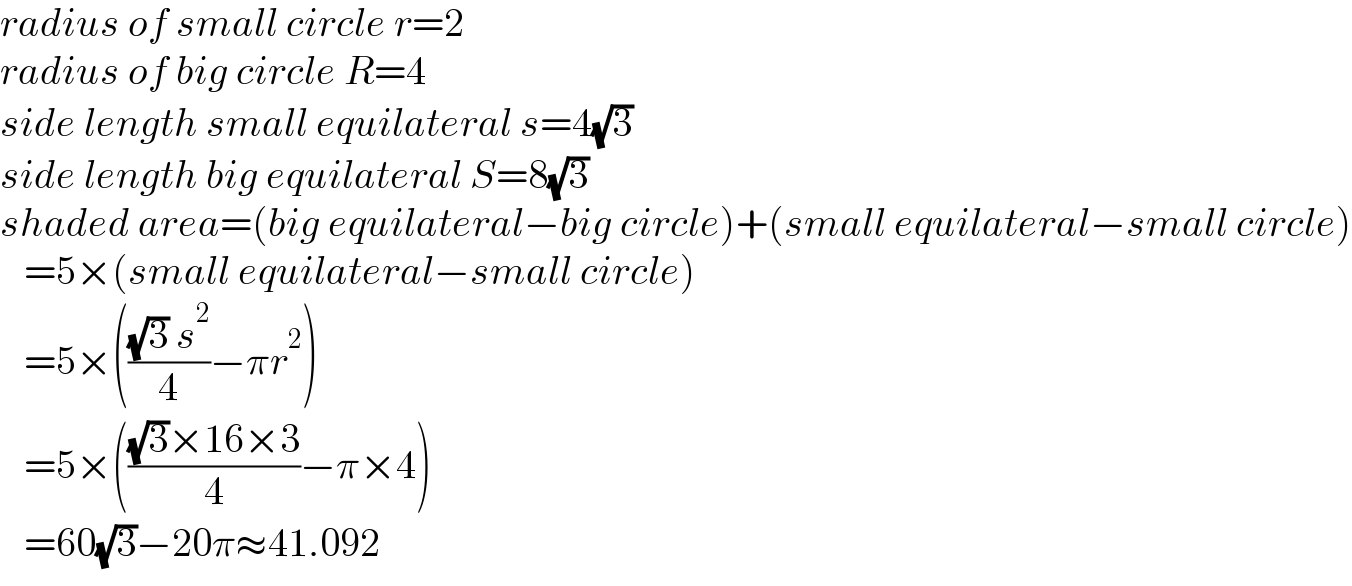
$${radius}\:{of}\:{small}\:{circle}\:{r}=\mathrm{2} \\ $$$${radius}\:{of}\:{big}\:{circle}\:{R}=\mathrm{4} \\ $$$${side}\:{length}\:{small}\:{equilateral}\:{s}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$${side}\:{length}\:{big}\:{equilateral}\:{S}=\mathrm{8}\sqrt{\mathrm{3}} \\ $$$${shaded}\:{area}=\left({big}\:{equilateral}−{big}\:{circle}\right)+\left({small}\:{equilateral}−{small}\:{circle}\right) \\ $$$$\:\:\:=\mathrm{5}×\left({small}\:{equilateral}−{small}\:{circle}\right) \\ $$$$\:\:\:=\mathrm{5}×\left(\frac{\sqrt{\mathrm{3}}\:{s}^{\mathrm{2}} }{\mathrm{4}}−\pi{r}^{\mathrm{2}} \right) \\ $$$$\:\:\:=\mathrm{5}×\left(\frac{\sqrt{\mathrm{3}}×\mathrm{16}×\mathrm{3}}{\mathrm{4}}−\pi×\mathrm{4}\right) \\ $$$$\:\:\:=\mathrm{60}\sqrt{\mathrm{3}}−\mathrm{20}\pi\approx\mathrm{41}.\mathrm{092} \\ $$
Commented by Rupesh123 last updated on 25/Feb/23
Excellent, sir!
