
Question Number 188016 by Rupesh123 last updated on 24/Feb/23

Answered by aleks041103 last updated on 24/Feb/23
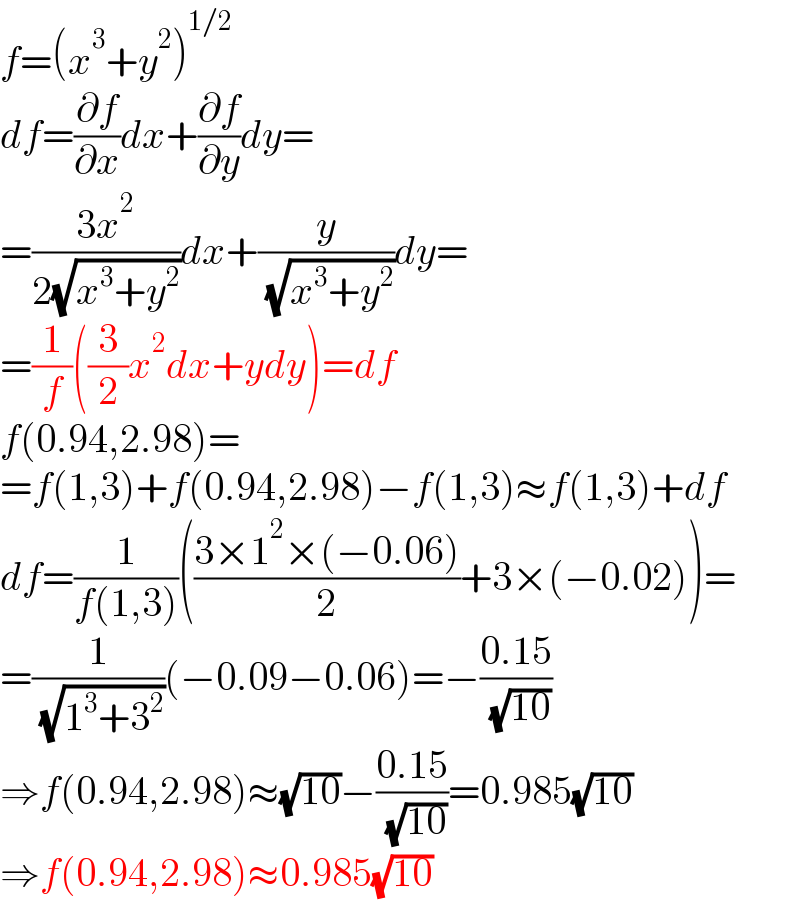
$${f}=\left({x}^{\mathrm{3}} +{y}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} \\ $$$${df}=\frac{\partial{f}}{\partial{x}}{dx}+\frac{\partial{f}}{\partial{y}}{dy}= \\ $$$$=\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{{x}^{\mathrm{3}} +{y}^{\mathrm{2}} }}{dx}+\frac{{y}}{\:\sqrt{{x}^{\mathrm{3}} +{y}^{\mathrm{2}} }}{dy}= \\ $$$$=\frac{\mathrm{1}}{{f}}\left(\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} {dx}+{ydy}\right)={df} \\ $$$${f}\left(\mathrm{0}.\mathrm{94},\mathrm{2}.\mathrm{98}\right)= \\ $$$$={f}\left(\mathrm{1},\mathrm{3}\right)+{f}\left(\mathrm{0}.\mathrm{94},\mathrm{2}.\mathrm{98}\right)−{f}\left(\mathrm{1},\mathrm{3}\right)\approx{f}\left(\mathrm{1},\mathrm{3}\right)+{df} \\ $$$${df}=\frac{\mathrm{1}}{{f}\left(\mathrm{1},\mathrm{3}\right)}\left(\frac{\mathrm{3}×\mathrm{1}^{\mathrm{2}} ×\left(−\mathrm{0}.\mathrm{06}\right)}{\mathrm{2}}+\mathrm{3}×\left(−\mathrm{0}.\mathrm{02}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}^{\mathrm{3}} +\mathrm{3}^{\mathrm{2}} }}\left(−\mathrm{0}.\mathrm{09}−\mathrm{0}.\mathrm{06}\right)=−\frac{\mathrm{0}.\mathrm{15}}{\:\sqrt{\mathrm{10}}} \\ $$$$\Rightarrow{f}\left(\mathrm{0}.\mathrm{94},\mathrm{2}.\mathrm{98}\right)\approx\sqrt{\mathrm{10}}−\frac{\mathrm{0}.\mathrm{15}}{\:\sqrt{\mathrm{10}}}=\mathrm{0}.\mathrm{985}\sqrt{\mathrm{10}} \\ $$$$\Rightarrow{f}\left(\mathrm{0}.\mathrm{94},\mathrm{2}.\mathrm{98}\right)\approx\mathrm{0}.\mathrm{985}\sqrt{\mathrm{10}} \\ $$
Commented by Rupesh123 last updated on 24/Feb/23
df = # dx + # dy is form of the answer Your answer should be in the form. So please check your answer for the df. Your second answer is correct
