Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 187989 by mnjuly1970 last updated on 24/Feb/23

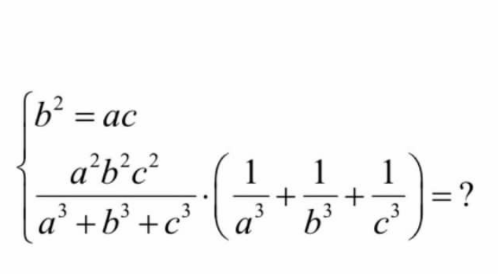
Answered by HeferH last updated on 24/Feb/23

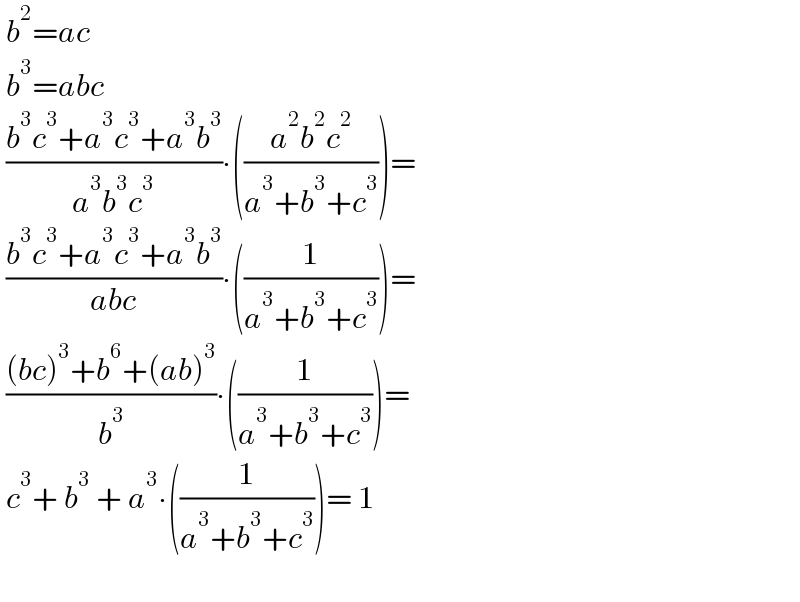
b^2 =ac b^3 =abc ((b^3 c^3 +a^3 c^3 +a^3 b^3 )/(a^3 b^3 c^3 ))∙(((a^2 b^2 c^2 )/(a^3 +b^3 +c^3 )))= ((b^3 c^3 +a^3 c^3 +a^3 b^3 )/(abc))∙((1/(a^3 +b^3 +c^3 )))= (((bc)^3 +b^6 +(ab)^3 )/b^3 )∙((1/(a^3 +b^3 +c^3 )))= c^3 + b^3 + a^3 ∙((1/(a^3 +b^3 +c^3 )))= 1

$$\:{b}^{\mathrm{2}} ={ac} \\ $$$$\:{b}^{\mathrm{3}} ={abc} \\ $$$$\:\frac{{b}^{\mathrm{3}} {c}^{\mathrm{3}} +{a}^{\mathrm{3}} {c}^{\mathrm{3}} +{a}^{\mathrm{3}} {b}^{\mathrm{3}} }{{a}^{\mathrm{3}} {b}^{\mathrm{3}} {c}^{\mathrm{3}} }\centerdot\left(\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\right)= \\ $$$$\:\frac{{b}^{\mathrm{3}} {c}^{\mathrm{3}} +{a}^{\mathrm{3}} {c}^{\mathrm{3}} +{a}^{\mathrm{3}} {b}^{\mathrm{3}} }{{abc}}\centerdot\left(\frac{\mathrm{1}}{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\right)= \\ $$$$\:\frac{\left({bc}\right)^{\mathrm{3}} +{b}^{\mathrm{6}} +\left({ab}\right)^{\mathrm{3}} }{{b}^{\mathrm{3}} }\centerdot\left(\frac{\mathrm{1}}{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\right)= \\ $$$$\:{c}^{\mathrm{3}} +\:{b}^{\mathrm{3}} \:+\:{a}^{\mathrm{3}} \centerdot\left(\frac{\mathrm{1}}{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\right)=\:\mathrm{1} \\ $$$$\: \\ $$

Answered by MathGuy last updated on 24/Feb/23

Answer :− ((a^2 b^2 c^2 )/(a^3 +b^3 +c^3 ))(((b^3 c^3 +c^3 a^3 +a^3 b^3 )/(a^3 b^3 c^3 ))) ⇒ (1/(a^3 +b^3 +c^3 ))(((b^3 c^3 +c^3 a^3 +a^3 b^3 )/(abc))) ⇒ (1/(a^3 +b^3 +c^3 ))(((b^2 c^2 )/a)+((c^2 a^2 )/b)+((a^2 b^2 )/c)) substitute b^2 =ac & c^2 a^2 =b^2 , in the expression under brackets and simplify. you will get (1/(a^3 +b^3 +c^3 ))(a^3 +b^3 +c^3 ) = 1

$${Answer}\::−\: \\ $$$$\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\left(\frac{{b}^{\mathrm{3}} {c}^{\mathrm{3}} +{c}^{\mathrm{3}} {a}^{\mathrm{3}} +{a}^{\mathrm{3}} {b}^{\mathrm{3}} }{{a}^{\mathrm{3}} {b}^{\mathrm{3}} {c}^{\mathrm{3}} }\right) \\ $$$$ \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\left(\frac{{b}^{\mathrm{3}} {c}^{\mathrm{3}} +{c}^{\mathrm{3}} {a}^{\mathrm{3}} +{a}^{\mathrm{3}} {b}^{\mathrm{3}} }{{abc}}\right) \\ $$$$ \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\left(\frac{{b}^{\mathrm{2}} {c}^{\mathrm{2}} }{{a}}+\frac{{c}^{\mathrm{2}} {a}^{\mathrm{2}} }{{b}}+\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{c}}\right) \\ $$$${substitute}\:{b}^{\mathrm{2}} ={ac}\:\&\:{c}^{\mathrm{2}} {a}^{\mathrm{2}} ={b}^{\mathrm{2}} ,\:{in}\:{the}\:{expression} \\ $$$${under}\:{brackets}\:{and}\:{simplify}. \\ $$$${you}\:{will}\:{get}\: \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right) \\ $$$$=\:\mathrm{1}\: \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com