Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

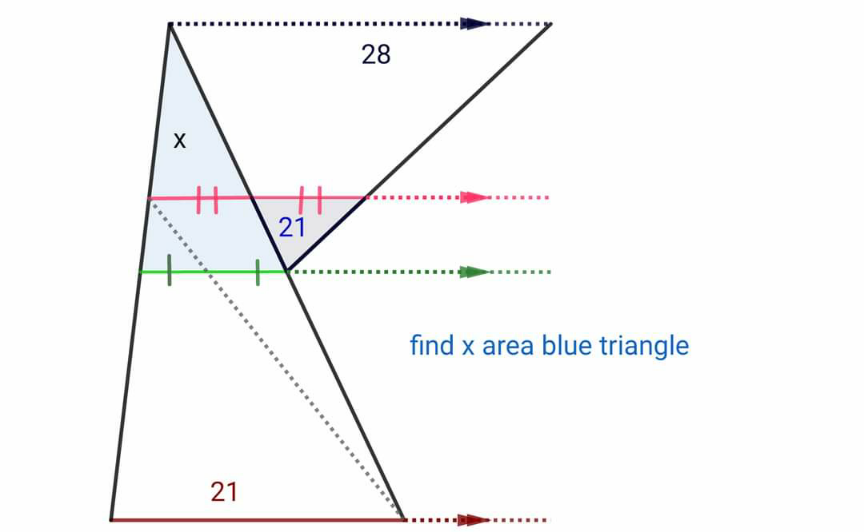
Question Number 187968 by normans last updated on 24/Feb/23

Commented by a.lgnaoui last updated on 24/Feb/23

21?

$$\mathrm{21}? \\ $$

Commented by a.lgnaoui last updated on 24/Feb/23

I think in top=21=mesure of line and down =(Area)

$${I}\:{think}\:\:{in}\:{top}=\mathrm{21}={mesure}\:{of}\:{line} \\ $$$${and}\:{down}\:=\left({Area}\right) \\ $$

Commented by a.lgnaoui last updated on 24/Feb/23

or the inverse

$${or}\:\:{the}\:{inverse} \\ $$

Commented by normans last updated on 25/Feb/23

no sir

$${no}\:{sir} \\ $$

Commented by mr W last updated on 25/Feb/23

wrong! even blind people can clearly see that blue area must be much bigger than the gray area 21. so 21 is clearly wrong. 100 is the right answer.

$${wrong}! \\ $$$${even}\:{blind}\:{people}\:{can}\:{clearly}\:{see}\:{that} \\ $$$${blue}\:{area}\:{must}\:{be}\:{much}\:{bigger}\:{than} \\ $$$${the}\:{gray}\:{area}\:\mathrm{21}.\:{so}\:\mathrm{21}\:{is}\:{clearly}\:{wrong}. \\ $$$$\mathrm{100}\:{is}\:{the}\:{right}\:{answer}. \\ $$

Answered by mr W last updated on 25/Feb/23

Commented by mr W last updated on 25/Feb/23

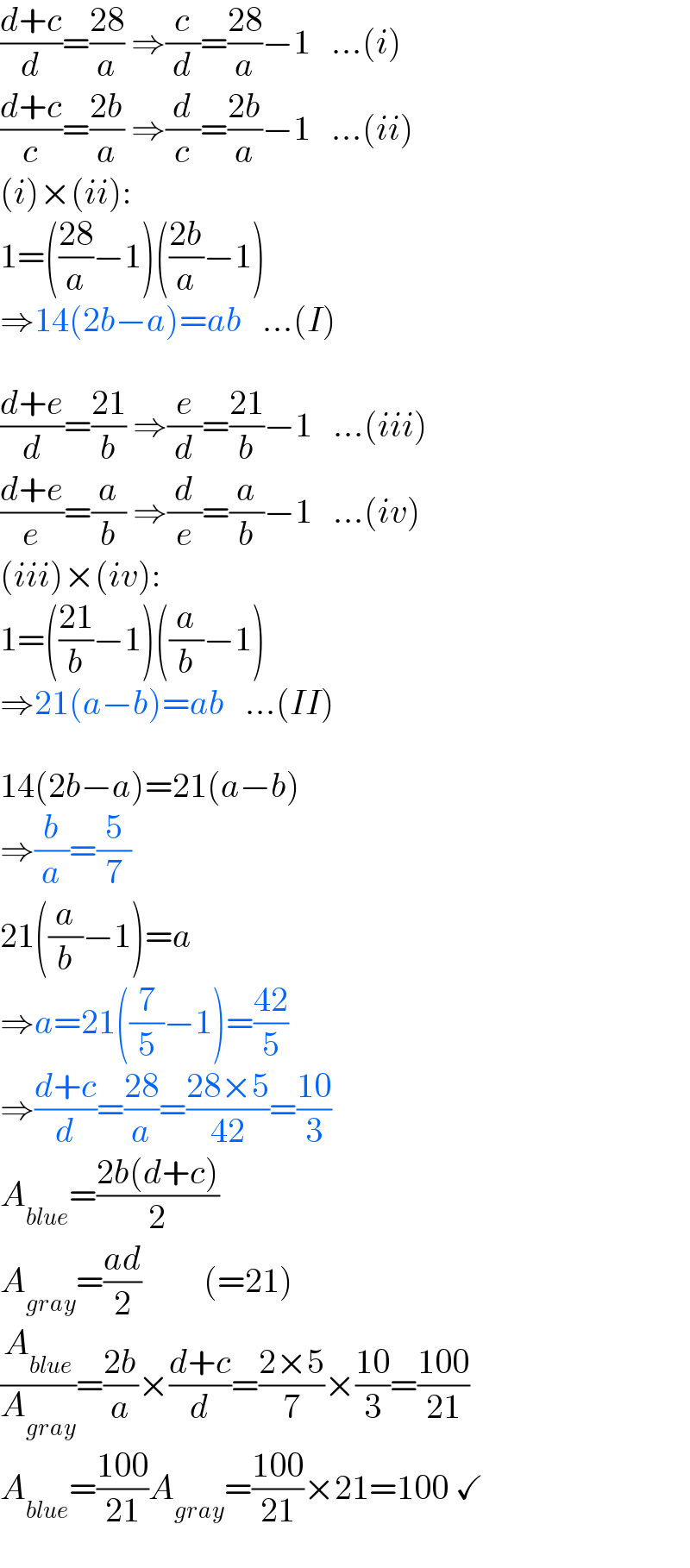
((d+c)/d)=((28)/a) ⇒(c/d)=((28)/a)−1 ...(i) ((d+c)/c)=((2b)/a) ⇒(d/c)=((2b)/a)−1 ...(ii) (i)×(ii): 1=(((28)/a)−1)(((2b)/a)−1) ⇒14(2b−a)=ab ...(I) ((d+e)/d)=((21)/b) ⇒(e/d)=((21)/b)−1 ...(iii) ((d+e)/e)=(a/b) ⇒(d/e)=(a/b)−1 ...(iv) (iii)×(iv): 1=(((21)/b)−1)((a/b)−1) ⇒21(a−b)=ab ...(II) 14(2b−a)=21(a−b) ⇒(b/a)=(5/7) 21((a/b)−1)=a ⇒a=21((7/5)−1)=((42)/5) ⇒((d+c)/d)=((28)/a)=((28×5)/(42))=((10)/3) A_(blue) =((2b(d+c))/2) A_(gray) =((ad)/2) (=21) (A_(blue) /A_(gray) )=((2b)/a)×((d+c)/d)=((2×5)/7)×((10)/3)=((100)/(21)) A_(blue) =((100)/(21))A_(gray) =((100)/(21))×21=100 ✓

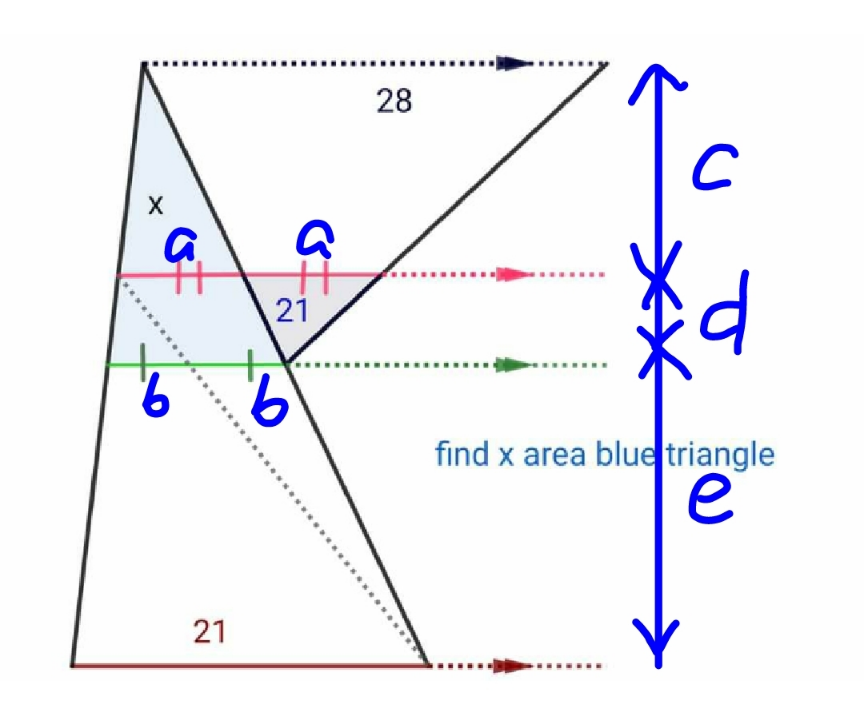
$$\frac{{d}+{c}}{{d}}=\frac{\mathrm{28}}{{a}}\:\Rightarrow\frac{{c}}{{d}}=\frac{\mathrm{28}}{{a}}−\mathrm{1}\:\:\:...\left({i}\right) \\ $$$$\frac{{d}+{c}}{{c}}=\frac{\mathrm{2}{b}}{{a}}\:\Rightarrow\frac{{d}}{{c}}=\frac{\mathrm{2}{b}}{{a}}−\mathrm{1}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\mathrm{1}=\left(\frac{\mathrm{28}}{{a}}−\mathrm{1}\right)\left(\frac{\mathrm{2}{b}}{{a}}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{14}\left(\mathrm{2}{b}−{a}\right)={ab}\:\:\:...\left({I}\right) \\ $$$$ \\ $$$$\frac{{d}+{e}}{{d}}=\frac{\mathrm{21}}{{b}}\:\Rightarrow\frac{{e}}{{d}}=\frac{\mathrm{21}}{{b}}−\mathrm{1}\:\:\:...\left({iii}\right) \\ $$$$\frac{{d}+{e}}{{e}}=\frac{{a}}{{b}}\:\Rightarrow\frac{{d}}{{e}}=\frac{{a}}{{b}}−\mathrm{1}\:\:\:...\left({iv}\right) \\ $$$$\left({iii}\right)×\left({iv}\right): \\ $$$$\mathrm{1}=\left(\frac{\mathrm{21}}{{b}}−\mathrm{1}\right)\left(\frac{{a}}{{b}}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{21}\left({a}−{b}\right)={ab}\:\:\:...\left({II}\right) \\ $$$$ \\ $$$$\mathrm{14}\left(\mathrm{2}{b}−{a}\right)=\mathrm{21}\left({a}−{b}\right) \\ $$$$\Rightarrow\frac{{b}}{{a}}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\mathrm{21}\left(\frac{{a}}{{b}}−\mathrm{1}\right)={a} \\ $$$$\Rightarrow{a}=\mathrm{21}\left(\frac{\mathrm{7}}{\mathrm{5}}−\mathrm{1}\right)=\frac{\mathrm{42}}{\mathrm{5}} \\ $$$$\Rightarrow\frac{{d}+{c}}{{d}}=\frac{\mathrm{28}}{{a}}=\frac{\mathrm{28}×\mathrm{5}}{\mathrm{42}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$${A}_{{blue}} =\frac{\mathrm{2}{b}\left({d}+{c}\right)}{\mathrm{2}} \\ $$$${A}_{{gray}} =\frac{{ad}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\left(=\mathrm{21}\right) \\ $$$$\frac{{A}_{{blue}} }{{A}_{{gray}} }=\frac{\mathrm{2}{b}}{{a}}×\frac{{d}+{c}}{{d}}=\frac{\mathrm{2}×\mathrm{5}}{\mathrm{7}}×\frac{\mathrm{10}}{\mathrm{3}}=\frac{\mathrm{100}}{\mathrm{21}} \\ $$$${A}_{{blue}} =\frac{\mathrm{100}}{\mathrm{21}}{A}_{{gray}} =\frac{\mathrm{100}}{\mathrm{21}}×\mathrm{21}=\mathrm{100}\:\checkmark \\ $$

Commented by normans last updated on 25/Feb/23

yes, this is the right solution I mean. Thanks Prof..

$$\boldsymbol{{yes}},\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\:\boldsymbol{{the}}\:\boldsymbol{{right}}\:\boldsymbol{{solution}}\:\boldsymbol{{I}}\:\boldsymbol{{mean}}. \\ $$$$\boldsymbol{{Thanks}}\:\boldsymbol{{Prof}}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com