
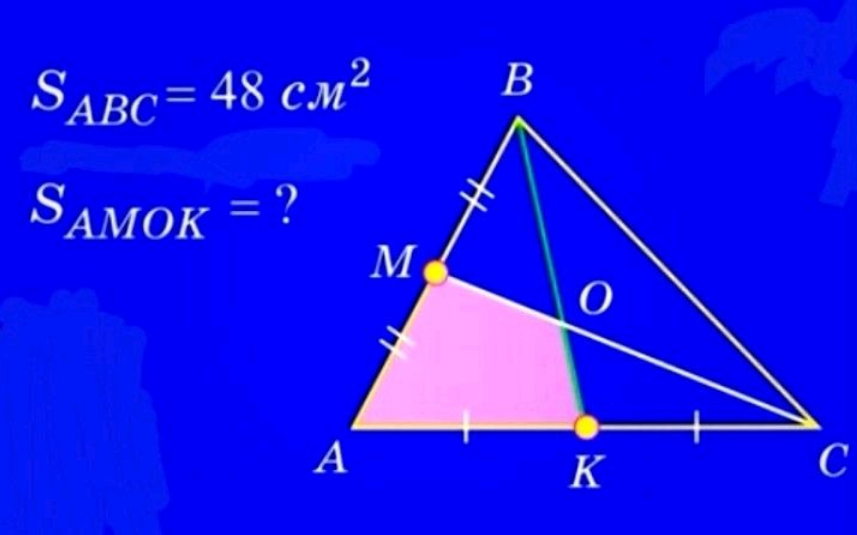
Question Number 187953 by Mingma last updated on 24/Feb/23
Answered by som(math1967) last updated on 24/Feb/23
![△AOB=△AOC=△AOC=(1/3)△ABC =(1/3)×48=16cm^2 △AOM=(1/2)△AOB=8cm^2 [OM is median of△AOB] △AOK=(1/2)△AOC=8cm^2 S_(AMOK) =△AOM+△AOK=8+8=16cm^2](Q187957.png)
$$\bigtriangleup{AOB}=\bigtriangleup{AOC}=\bigtriangleup{AOC}=\frac{\mathrm{1}}{\mathrm{3}}\bigtriangleup{ABC} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{48}=\mathrm{16}{cm}^{\mathrm{2}} \\ $$$$\bigtriangleup{AOM}=\frac{\mathrm{1}}{\mathrm{2}}\bigtriangleup{AOB}=\mathrm{8}{cm}^{\mathrm{2}} \\ $$$$\left[{OM}\:{is}\:{median}\:{of}\bigtriangleup{AOB}\right] \\ $$$$\bigtriangleup{AOK}=\frac{\mathrm{1}}{\mathrm{2}}\bigtriangleup{AOC}=\mathrm{8}{cm}^{\mathrm{2}} \\ $$$${S}_{{AMOK}} =\bigtriangleup{AOM}+\bigtriangleup{AOK}=\mathrm{8}+\mathrm{8}=\mathrm{16}{cm}^{\mathrm{2}} \\ $$
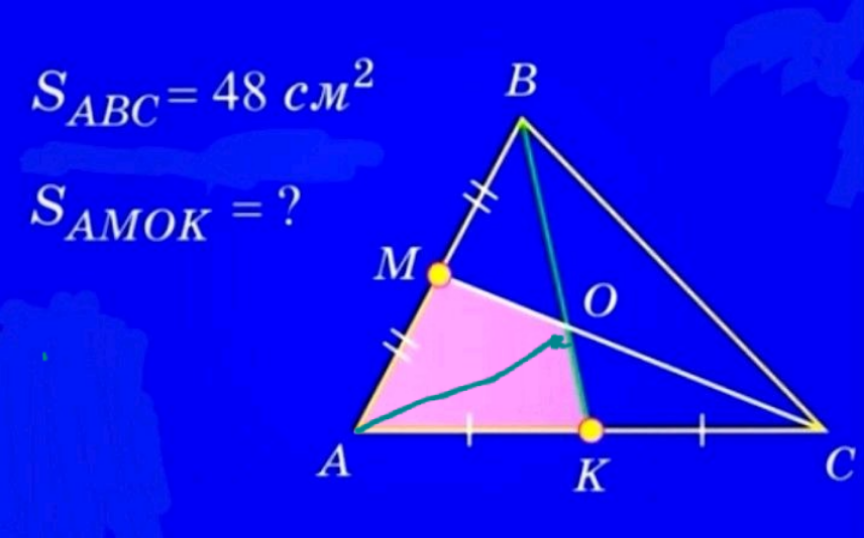
Commented by som(math1967) last updated on 24/Feb/23
Commented by Mingma last updated on 24/Feb/23
Very nice, sir!
Answered by HeferH last updated on 24/Feb/23

$$\mathrm{2}\left(\frac{{S}_{{ABC}} }{\mathrm{6}}\right)\:=\:{S}_{{AMOK}} \\ $$$$\:{S}_{{AMOK}\:} =\:\mathrm{16}{cm}^{\mathrm{2}} \\ $$
