Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

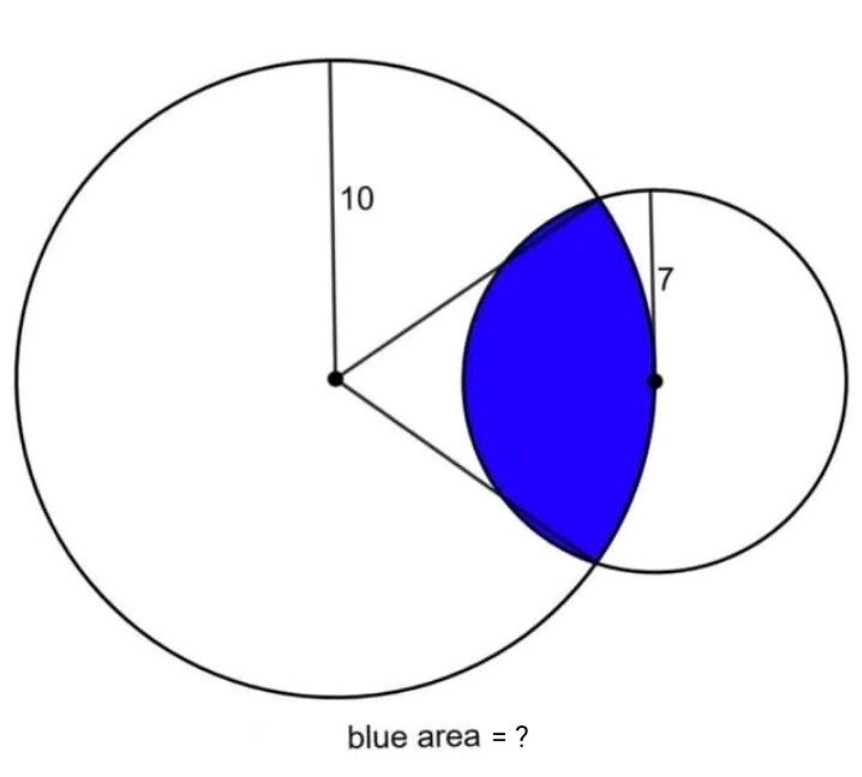
Question Number 187932 by Rupesh123 last updated on 23/Feb/23

Answered by a.lgnaoui last updated on 24/Feb/23

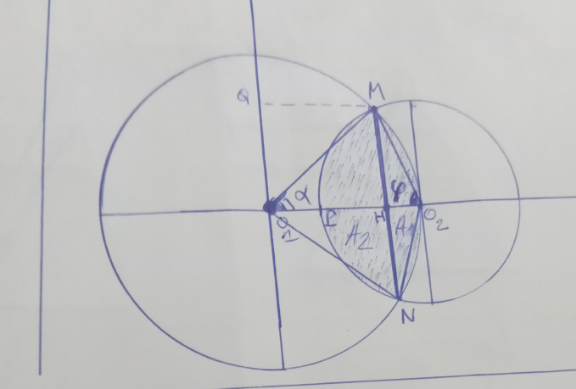
O_1 :centre du cercle(C_1 )= origine Ref Cercles( C_1 )et(C_2 )d equations { ((x^2 +y_1 ^2 =100 (1))),(((x−10)^2 +y_2 ^2 =49 (2))) :} Ponts communs(M; N )definies par y_1 =y_2 ⇒ x=((151)/(20)) O_1 H=7,55 y=(√(100−((151^2 )/(20^2 )))) =±(√(43)) MH=O_1 Q=6,55724 Aire(Bleu) limite par C_1 erC_2 A=A_1 +A_2 tan α=((OQ)/(OH))= ((20(√(43)))/(151))⇒ [α=41°] Aire[A_1 ]=[αR_1 ^2 −O_1 H ×MH] α=((41π)/(180)) A_1 =((5×41π)/9)−49,5) Aire A_1 =22 Aire A_2 =ϕR_2 ^2 −O_2 H×MH O_2 H=OO−O_1 H=2,45⇒ tan ϕ=((MH)/(O_2 H)) ⇒ϕ≅ ((23π)/(60)) ⇒ AireA_2 =((49×23π)/(60)) −16=43 A=A_1 +A_2 Aire Totale=65 Totale generale Aire= 65+(αR_1 ^2 +ϕR_2 ^2 ) =65+131=196

$${O}_{\mathrm{1}} :{centre}\:{du}\:{cercle}\left({C}_{\mathrm{1}} \right)=\:\:\:{origine}\:{Ref} \\ $$$${Cercles}\left(\:{C}_{\mathrm{1}} \:\right){et}\left({C}_{\mathrm{2}} \right){d}\:{equations}\: \\ $$$$\begin{cases}{{x}^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{100}\:\:\left(\mathrm{1}\right)}\\{\left({x}−\mathrm{10}\right)^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{49}\:\:\:\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$${Ponts}\:{communs}\left({M};\:{N}\:\right){definies}\:{par} \\ $$$${y}_{\mathrm{1}} ={y}_{\mathrm{2}} \Rightarrow\:\:\:\:{x}=\frac{\mathrm{151}}{\mathrm{20}}\:\:\:\:\:\:\:{O}_{\mathrm{1}} {H}=\mathrm{7},\mathrm{55}\:\: \\ $$$${y}=\sqrt{\mathrm{100}−\frac{\mathrm{151}^{\mathrm{2}} }{\mathrm{20}^{\mathrm{2}} }}\:=\pm\sqrt{\mathrm{43}}\:\:\:\:{MH}={O}_{\mathrm{1}} {Q}=\mathrm{6},\mathrm{55724} \\ $$$${Aire}\left({Bleu}\right)\:{limite}\:{par}\:{C}_{\mathrm{1}} \:{erC}_{\mathrm{2}} \\ $$$${A}={A}_{\mathrm{1}} +{A}_{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\frac{{OQ}}{{OH}}=\:\frac{\mathrm{20}\sqrt{\mathrm{43}}}{\mathrm{151}}\Rightarrow\:\:\:\left[\alpha=\mathrm{41}°\right] \\ $$$${Aire}\left[{A}_{\mathrm{1}} \right]=\left[\alpha{R}_{\mathrm{1}} ^{\mathrm{2}} −{O}_{\mathrm{1}} {H}\:×{MH}\right]\:\:\:\alpha=\frac{\mathrm{41}\pi}{\mathrm{180}} \\ $$$$\left.{A}_{\mathrm{1}} =\frac{\mathrm{5}×\mathrm{41}\pi}{\mathrm{9}}−\mathrm{49},\mathrm{5}\right)\:\:\:\:\boldsymbol{{Aire}}\:\boldsymbol{{A}}_{\mathrm{1}} =\mathrm{22} \\ $$$$ \\ $$$${Aire}\:{A}_{\mathrm{2}} =\varphi{R}_{\mathrm{2}} ^{\mathrm{2}} −{O}_{\mathrm{2}} {H}×{MH}\:\:\: \\ $$$$\:{O}_{\mathrm{2}} {H}={OO}−{O}_{\mathrm{1}} {H}=\mathrm{2},\mathrm{45}\Rightarrow\:\:\mathrm{tan}\:\varphi=\frac{{MH}}{{O}_{\mathrm{2}} {H}}\: \\ $$$$\Rightarrow\varphi\cong\:\:\frac{\mathrm{23}\pi}{\mathrm{60}}\:\Rightarrow\:\:\boldsymbol{{A}}{ireA}_{\mathrm{2}} =\frac{\mathrm{49}×\mathrm{23}\pi}{\mathrm{60}}\:−\mathrm{16}=\mathrm{43} \\ $$$$\:\:\:\boldsymbol{{A}}=\boldsymbol{{A}}_{\mathrm{1}} +\boldsymbol{{A}}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{Aire}}\:\boldsymbol{{Totale}}=\mathrm{65} \\ $$$$ \\ $$$$\:\:\:\:{Totale}\:{generale} \\ $$$${A}\boldsymbol{{ire}}=\:\:\mathrm{65}+\left(\alpha{R}_{\mathrm{1}} ^{\mathrm{2}} +\varphi{R}_{\mathrm{2}} ^{\mathrm{2}} \right) \\ $$$$\:\:\:\:=\mathrm{65}+\mathrm{131}=\mathrm{196} \\ $$$$ \\ $$$$\:\: \\ $$

Commented by a.lgnaoui last updated on 25/Feb/23

Answered by mr W last updated on 24/Feb/23

Commented by mr W last updated on 24/Feb/23

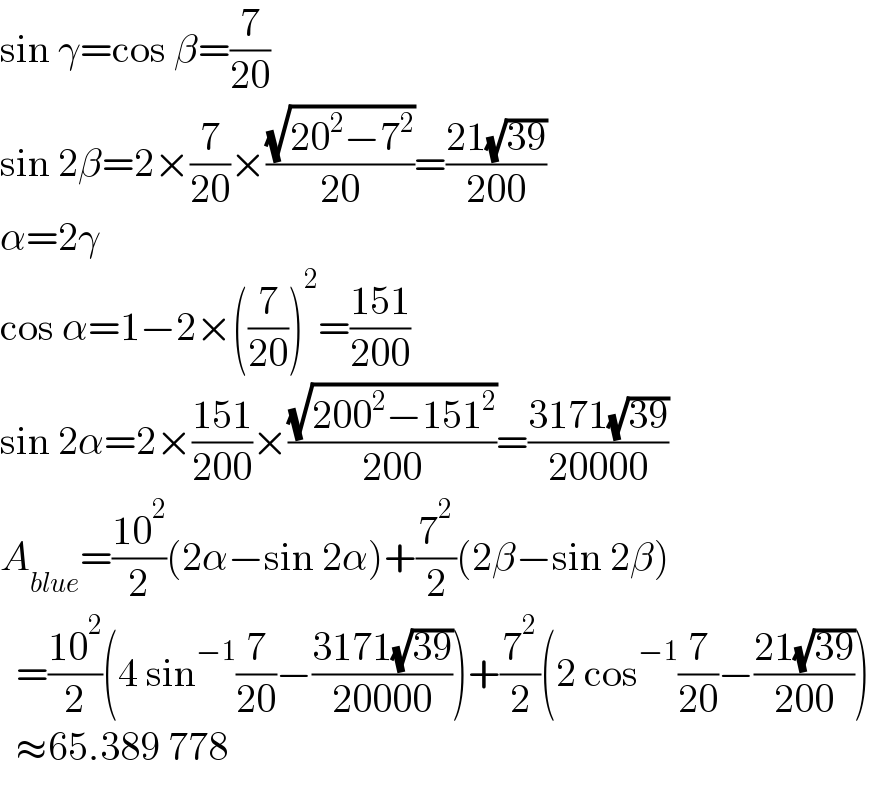
sin γ=cos β=(7/(20)) sin 2β=2×(7/(20))×((√(20^2 −7^2 ))/(20))=((21(√(39)))/(200)) α=2γ cos α=1−2×((7/(20)))^2 =((151)/(200)) sin 2α=2×((151)/(200))×((√(200^2 −151^2 ))/(200))=((3171(√(39)))/(20000)) A_(blue) =((10^2 )/2)(2α−sin 2α)+(7^2 /2)(2β−sin 2β) =((10^2 )/2)(4 sin^(−1) (7/(20))−((3171(√(39)))/(20000)))+(7^2 /2)(2 cos^(−1) (7/(20))−((21(√(39)))/(200))) ≈65.389 778

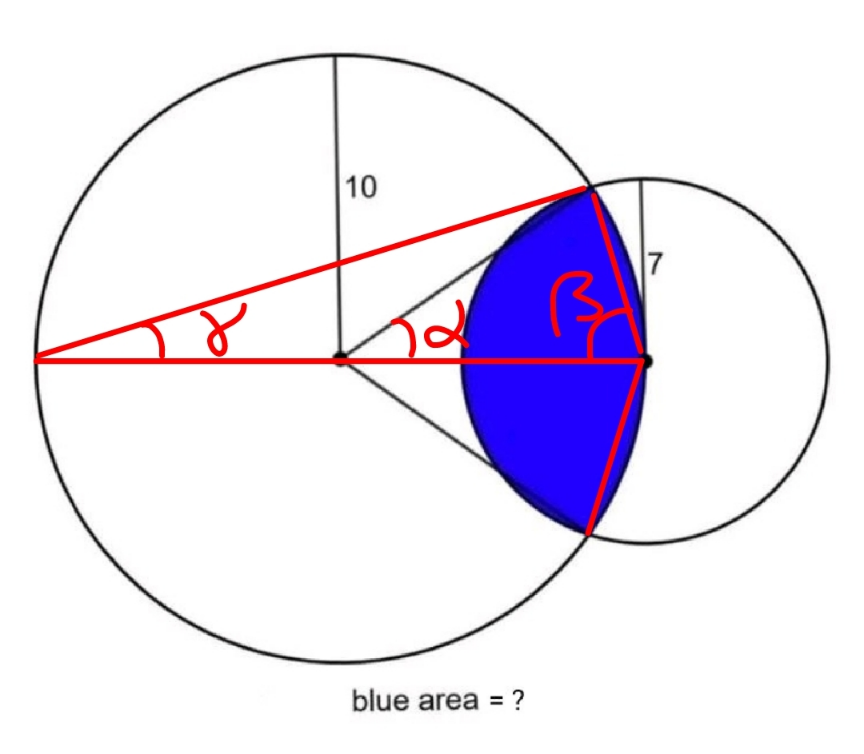
$$\mathrm{sin}\:\gamma=\mathrm{cos}\:\beta=\frac{\mathrm{7}}{\mathrm{20}} \\ $$$$\mathrm{sin}\:\mathrm{2}\beta=\mathrm{2}×\frac{\mathrm{7}}{\mathrm{20}}×\frac{\sqrt{\mathrm{20}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }}{\mathrm{20}}=\frac{\mathrm{21}\sqrt{\mathrm{39}}}{\mathrm{200}} \\ $$$$\alpha=\mathrm{2}\gamma \\ $$$$\mathrm{cos}\:\alpha=\mathrm{1}−\mathrm{2}×\left(\frac{\mathrm{7}}{\mathrm{20}}\right)^{\mathrm{2}} =\frac{\mathrm{151}}{\mathrm{200}} \\ $$$$\mathrm{sin}\:\mathrm{2}\alpha=\mathrm{2}×\frac{\mathrm{151}}{\mathrm{200}}×\frac{\sqrt{\mathrm{200}^{\mathrm{2}} −\mathrm{151}^{\mathrm{2}} }}{\mathrm{200}}=\frac{\mathrm{3171}\sqrt{\mathrm{39}}}{\mathrm{20000}} \\ $$$${A}_{{blue}} =\frac{\mathrm{10}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\alpha−\mathrm{sin}\:\mathrm{2}\alpha\right)+\frac{\mathrm{7}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\beta−\mathrm{sin}\:\mathrm{2}\beta\right) \\ $$$$\:\:=\frac{\mathrm{10}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{4}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{20}}−\frac{\mathrm{3171}\sqrt{\mathrm{39}}}{\mathrm{20000}}\right)+\frac{\mathrm{7}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{20}}−\frac{\mathrm{21}\sqrt{\mathrm{39}}}{\mathrm{200}}\right) \\ $$$$\:\:\approx\mathrm{65}.\mathrm{389}\:\mathrm{778} \\ $$

Commented by Rupesh123 last updated on 01/Mar/23

Excellent!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com