Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 187811 by Rupesh123 last updated on 22/Feb/23

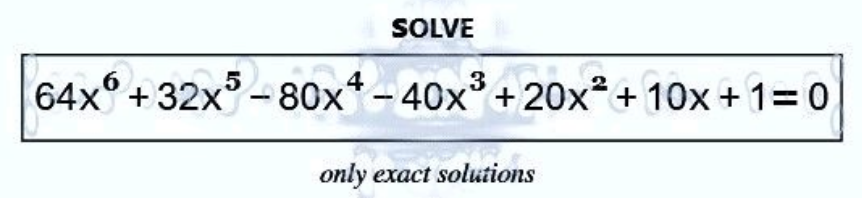
Answered by Frix last updated on 22/Feb/23

x^6 +(x^5 /2)−((5x^4 )/4)−((5x^3 )/8)+((5x^2 )/(16))+((5x)/(32))+(1/(64))=0 Try to find 2 cubic factors. If it′s possible to solve I guess the constant factors must be ±(√(1/(64)))=±(1/8): let s∈{−1, 1} (x^3 +ax^2 +bx+(s/8))(x^3 +cx^2 +dx+(s/8))=0 By matching the coefficients we get a=0 b=−(3/4) c=(1/2) d=−(1/2) s=−1 ⇒ (x^3 −((3x)/4)−(1/8))(x^3 +(x^2 /2)−(x/2)−(1/8))=0 We can solve these: x_1 =−cos ((2π)/9) x_2 =−sin (π/(18)) x_3 =cos (π/9) x_4 =−cos (π/7) x_5 =−sin (π/(14)) x_6 =sin ((3π)/(14))

$${x}^{\mathrm{6}} +\frac{{x}^{\mathrm{5}} }{\mathrm{2}}−\frac{\mathrm{5}{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{5}{x}^{\mathrm{3}} }{\mathrm{8}}+\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{5}{x}}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{64}}=\mathrm{0} \\ $$$$\mathrm{Try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{2}\:\mathrm{cubic}\:\mathrm{factors}.\:\mathrm{If}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible} \\ $$$$\mathrm{to}\:\mathrm{solve}\:\mathrm{I}\:\mathrm{guess}\:\mathrm{the}\:\mathrm{constant}\:\mathrm{factors}\:\mathrm{must} \\ $$$$\mathrm{be}\:\pm\sqrt{\frac{\mathrm{1}}{\mathrm{64}}}=\pm\frac{\mathrm{1}}{\mathrm{8}}:\:\mathrm{let}\:{s}\in\left\{−\mathrm{1},\:\mathrm{1}\right\} \\ $$$$\left({x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+\frac{{s}}{\mathrm{8}}\right)\left({x}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+\frac{{s}}{\mathrm{8}}\right)=\mathrm{0} \\ $$$$\mathrm{By}\:\mathrm{matching}\:\mathrm{the}\:\mathrm{coefficients}\:\mathrm{we}\:\mathrm{get} \\ $$$${a}=\mathrm{0}\:\:\:\:{b}=−\frac{\mathrm{3}}{\mathrm{4}}\:\:\:\:{c}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:{d}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:{s}=−\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\left({x}^{\mathrm{3}} −\frac{\mathrm{3}{x}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}\right)\left({x}^{\mathrm{3}} +\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\right)=\mathrm{0} \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{these}: \\ $$$${x}_{\mathrm{1}} =−\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{9}}\:\:\:\:{x}_{\mathrm{2}} =−\mathrm{sin}\:\frac{\pi}{\mathrm{18}}\:\:\:\:{x}_{\mathrm{3}} =\mathrm{cos}\:\frac{\pi}{\mathrm{9}} \\ $$$${x}_{\mathrm{4}} =−\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\:\:\:\:{x}_{\mathrm{5}} =−\mathrm{sin}\:\frac{\pi}{\mathrm{14}}\:\:\:\:{x}_{\mathrm{6}} =\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{14}} \\ $$

Commented by Rupesh123 last updated on 22/Feb/23

Great!

Commented by Frix last updated on 22/Feb/23

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com