Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

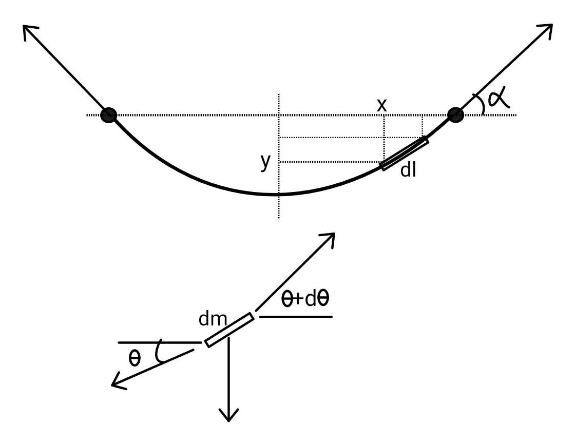
Question Number 187789 by ajfour last updated on 21/Feb/23

Answered by mahdipoor last updated on 22/Feb/23

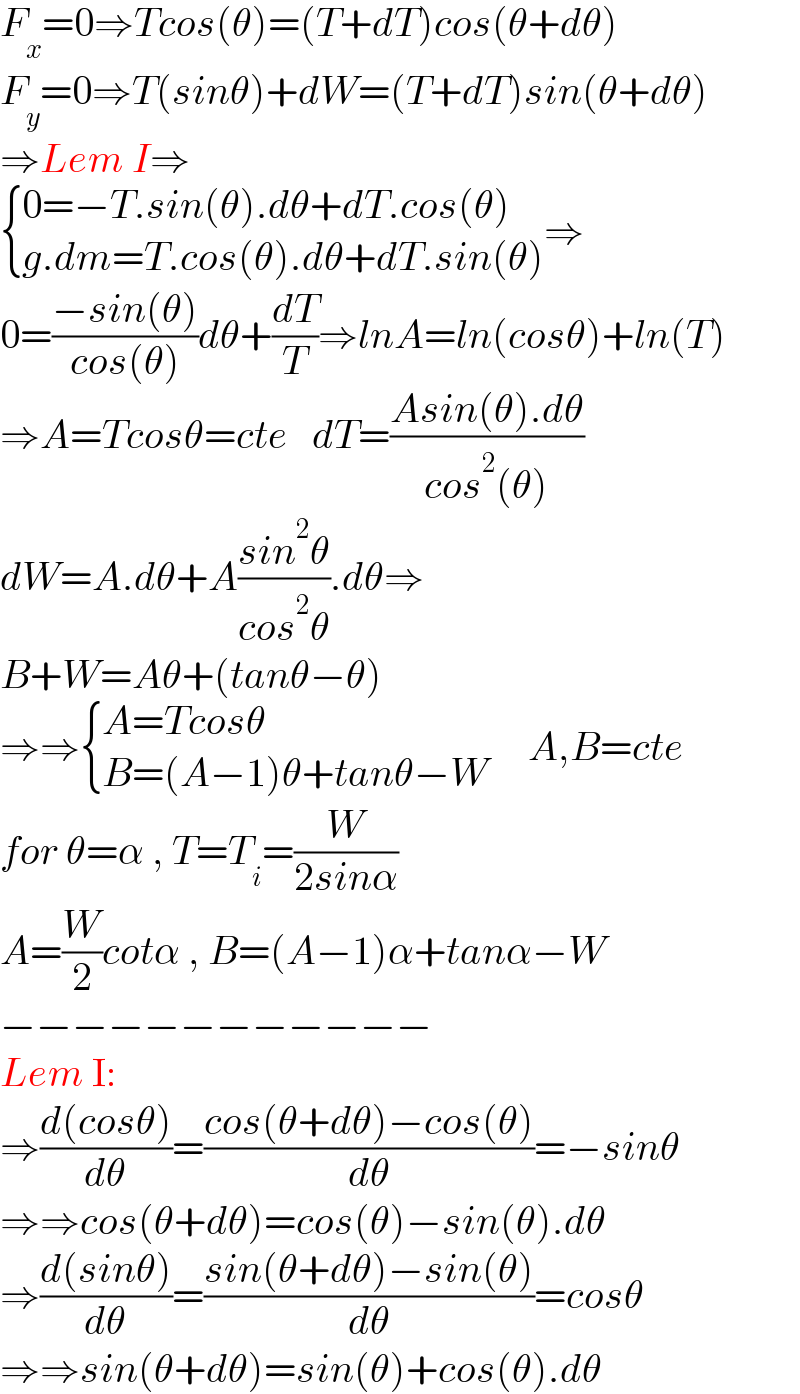
F_x =0⇒Tcos(θ)=(T+dT)cos(θ+dθ) F_y =0⇒T(sinθ)+dW=(T+dT)sin(θ+dθ) ⇒Lem I⇒ { ((0=−T.sin(θ).dθ+dT.cos(θ))),((g.dm=T.cos(θ).dθ+dT.sin(θ))) :}⇒ 0=((−sin(θ))/(cos(θ)))dθ+(dT/T)⇒lnA=ln(cosθ)+ln(T) ⇒A=Tcosθ=cte dT=((Asin(θ).dθ)/(cos^2 (θ))) dW=A.dθ+A((sin^2 θ)/(cos^2 θ)).dθ⇒ B+W=Aθ+(tanθ−θ) ⇒⇒ { ((A=Tcosθ)),((B=(A−1)θ+tanθ−W)) :} A,B=cte for θ=α , T=T_i =(W/(2sinα)) A=(W/2)cotα , B=(A−1)α+tanα−W −−−−−−−−−−−− Lem I: ⇒((d(cosθ))/dθ)=((cos(θ+dθ)−cos(θ))/dθ)=−sinθ ⇒⇒cos(θ+dθ)=cos(θ)−sin(θ).dθ ⇒((d(sinθ))/dθ)=((sin(θ+dθ)−sin(θ))/dθ)=cosθ ⇒⇒sin(θ+dθ)=sin(θ)+cos(θ).dθ

$${F}_{{x}} =\mathrm{0}\Rightarrow{Tcos}\left(\theta\right)=\left({T}+{dT}\right){cos}\left(\theta+{d}\theta\right) \\ $$$${F}_{{y}} =\mathrm{0}\Rightarrow{T}\left({sin}\theta\right)+{dW}=\left({T}+{dT}\right){sin}\left(\theta+{d}\theta\right) \\ $$$$\Rightarrow{Lem}\:{I}\Rightarrow \\ $$$$\begin{cases}{\mathrm{0}=−{T}.{sin}\left(\theta\right).{d}\theta+{dT}.{cos}\left(\theta\right)}\\{{g}.{dm}={T}.{cos}\left(\theta\right).{d}\theta+{dT}.{sin}\left(\theta\right)}\end{cases}\Rightarrow \\ $$$$\mathrm{0}=\frac{−{sin}\left(\theta\right)}{{cos}\left(\theta\right)}{d}\theta+\frac{{dT}}{{T}}\Rightarrow{lnA}={ln}\left({cos}\theta\right)+{ln}\left({T}\right) \\ $$$$\Rightarrow{A}={Tcos}\theta={cte}\:\:\:{dT}=\frac{{Asin}\left(\theta\right).{d}\theta}{{cos}^{\mathrm{2}} \left(\theta\right)} \\ $$$${dW}={A}.{d}\theta+{A}\frac{{sin}^{\mathrm{2}} \theta}{{cos}^{\mathrm{2}} \theta}.{d}\theta\Rightarrow \\ $$$${B}+{W}={A}\theta+\left({tan}\theta−\theta\right) \\ $$$$\Rightarrow\Rightarrow\begin{cases}{{A}={Tcos}\theta}\\{{B}=\left({A}−\mathrm{1}\right)\theta+{tan}\theta−{W}}\end{cases}\:\:\:\:\:{A},{B}={cte} \\ $$$${for}\:\theta=\alpha\:,\:{T}={T}_{{i}} =\frac{{W}}{\mathrm{2}{sin}\alpha} \\ $$$${A}=\frac{{W}}{\mathrm{2}}{cot}\alpha\:,\:{B}=\left({A}−\mathrm{1}\right)\alpha+{tan}\alpha−{W} \\ $$$$−−−−−−−−−−−− \\ $$$${Lem}\:\mathrm{I}: \\ $$$$\Rightarrow\frac{{d}\left({cos}\theta\right)}{{d}\theta}=\frac{{cos}\left(\theta+{d}\theta\right)−{cos}\left(\theta\right)}{{d}\theta}=−{sin}\theta \\ $$$$\Rightarrow\Rightarrow{cos}\left(\theta+{d}\theta\right)={cos}\left(\theta\right)−{sin}\left(\theta\right).{d}\theta \\ $$$$\Rightarrow\frac{{d}\left({sin}\theta\right)}{{d}\theta}=\frac{{sin}\left(\theta+{d}\theta\right)−{sin}\left(\theta\right)}{{d}\theta}={cos}\theta \\ $$$$\Rightarrow\Rightarrow{sin}\left(\theta+{d}\theta\right)={sin}\left(\theta\right)+{cos}\left(\theta\right).{d}\theta \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com