
Question Number 187589 by Mingma last updated on 19/Feb/23

Commented by Mingma last updated on 19/Feb/23
Blue area=?
Answered by cortano12 last updated on 19/Feb/23
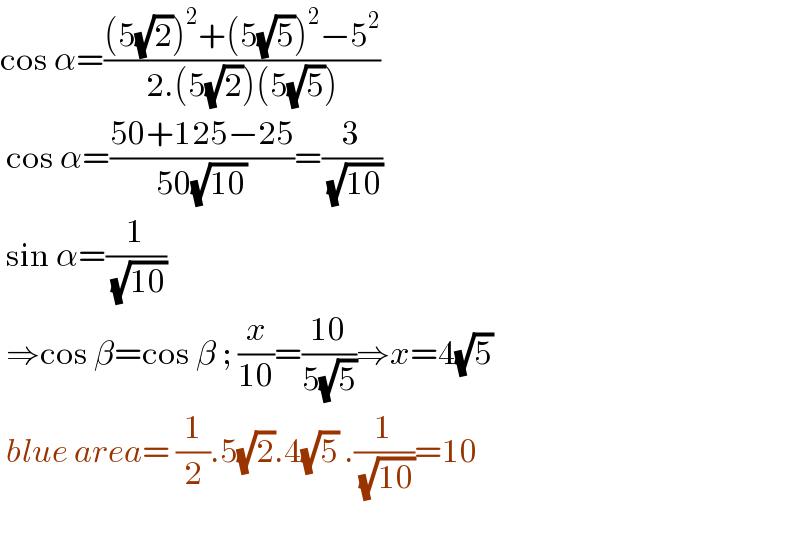
$$\mathrm{cos}\:\alpha=\frac{\left(\mathrm{5}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{5}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}.\left(\mathrm{5}\sqrt{\mathrm{2}}\right)\left(\mathrm{5}\sqrt{\mathrm{5}}\right)} \\ $$$$\:\mathrm{cos}\:\alpha=\frac{\mathrm{50}+\mathrm{125}−\mathrm{25}}{\mathrm{50}\sqrt{\mathrm{10}}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}} \\ $$$$\:\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}} \\ $$$$\:\Rightarrow\mathrm{cos}\:\beta=\mathrm{cos}\:\beta\:;\:\frac{{x}}{\mathrm{10}}=\frac{\mathrm{10}}{\mathrm{5}\sqrt{\mathrm{5}}}\Rightarrow{x}=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\:{blue}\:{area}=\:\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{5}\sqrt{\mathrm{2}}.\mathrm{4}\sqrt{\mathrm{5}}\:.\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}=\mathrm{10} \\ $$$$\: \\ $$
Commented by Mingma last updated on 19/Feb/23
Good!
Answered by mr W last updated on 19/Feb/23
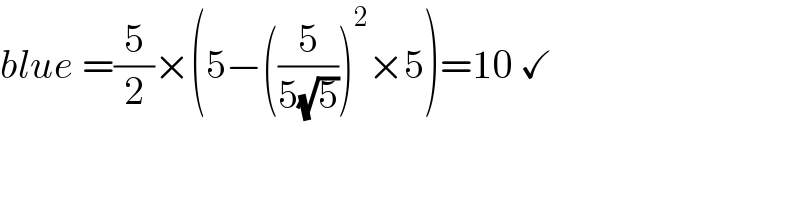
$${blue}\:=\frac{\mathrm{5}}{\mathrm{2}}×\left(\mathrm{5}−\left(\frac{\mathrm{5}}{\mathrm{5}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} ×\mathrm{5}\right)=\mathrm{10}\:\checkmark \\ $$
Commented by Mingma last updated on 19/Feb/23
Good!
Answered by HeferH last updated on 19/Feb/23

Commented by HeferH last updated on 19/Feb/23
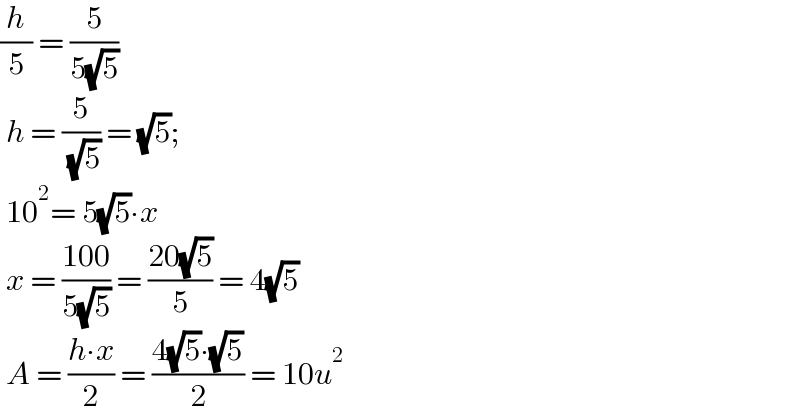
$$\frac{{h}}{\mathrm{5}}\:=\:\frac{\mathrm{5}}{\mathrm{5}\sqrt{\mathrm{5}}} \\ $$$$\:{h}\:=\:\frac{\mathrm{5}}{\:\sqrt{\mathrm{5}}}\:=\:\sqrt{\mathrm{5}};\: \\ $$$$\:\mathrm{10}^{\mathrm{2}} =\:\mathrm{5}\sqrt{\mathrm{5}}\centerdot{x} \\ $$$$\:{x}\:=\:\frac{\mathrm{100}}{\mathrm{5}\sqrt{\mathrm{5}}}\:=\:\frac{\mathrm{20}\sqrt{\mathrm{5}}}{\mathrm{5}}\:=\:\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\:{A}\:=\:\frac{{h}\centerdot{x}}{\mathrm{2}}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{5}}\centerdot\sqrt{\mathrm{5}}}{\mathrm{2}}\:=\:\mathrm{10}{u}^{\mathrm{2}} \\ $$
