Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 187557 by Rupesh123 last updated on 18/Feb/23

Answered by HeferH last updated on 19/Feb/23

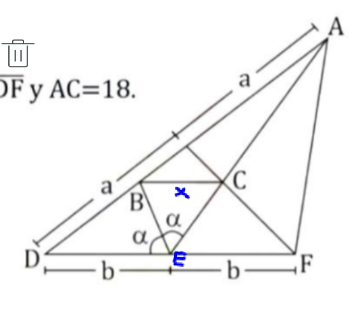
Commented by HeferH last updated on 19/Feb/23

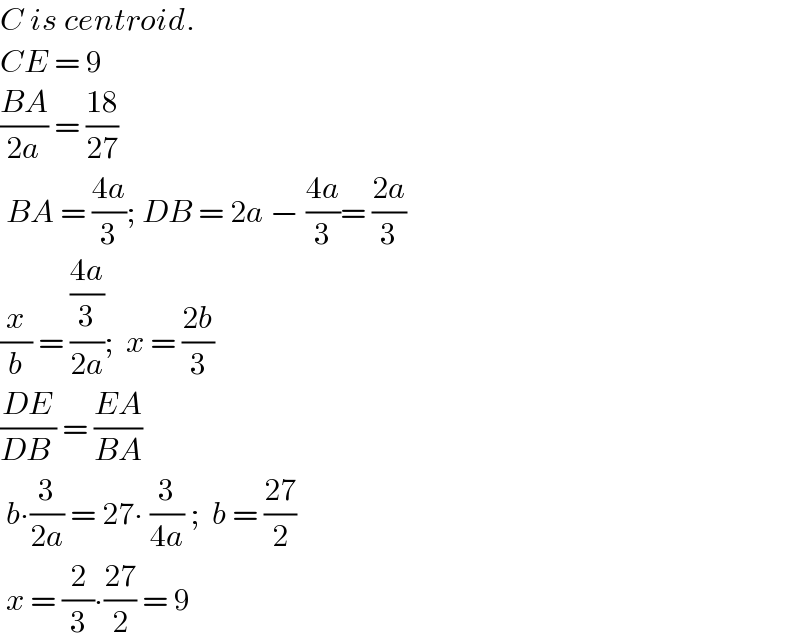
C is centroid. CE = 9 ((BA)/(2a)) = ((18)/(27)) BA = ((4a)/3); DB = 2a − ((4a)/3)= ((2a)/3) (x/b) = (((4a)/3)/(2a)); x = ((2b)/3) ((DE)/(DB )) = ((EA)/(BA)) b∙(3/(2a)) = 27∙ (3/(4a)) ; b = ((27)/2) x = (2/3)∙((27)/2) = 9

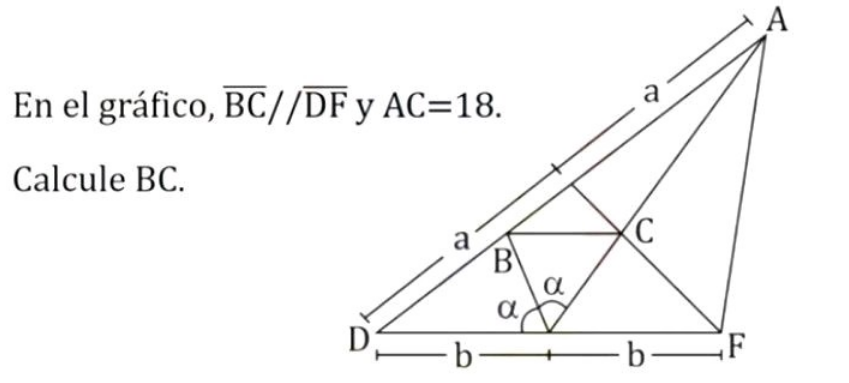
$${C}\:{is}\:{centroid}. \\ $$$${CE}\:=\:\mathrm{9}\: \\ $$$$\frac{{BA}}{\mathrm{2}{a}}\:=\:\frac{\mathrm{18}}{\mathrm{27}} \\ $$$$\:{BA}\:=\:\frac{\mathrm{4}{a}}{\mathrm{3}};\:{DB}\:=\:\mathrm{2}{a}\:−\:\frac{\mathrm{4}{a}}{\mathrm{3}}=\:\frac{\mathrm{2}{a}}{\mathrm{3}} \\ $$$$\frac{{x}}{{b}}\:=\:\frac{\frac{\mathrm{4}{a}}{\mathrm{3}}}{\mathrm{2}{a}};\:\:{x}\:=\:\frac{\mathrm{2}{b}}{\mathrm{3}} \\ $$$$\frac{{DE}}{{DB}\:}\:=\:\frac{{EA}}{{BA}}\: \\ $$$$\:{b}\centerdot\frac{\mathrm{3}}{\mathrm{2}{a}}\:=\:\mathrm{27}\centerdot\:\frac{\mathrm{3}}{\mathrm{4}{a}}\:;\:\:{b}\:=\:\frac{\mathrm{27}}{\mathrm{2}} \\ $$$$\:{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\mathrm{27}}{\mathrm{2}}\:=\:\mathrm{9}\: \\ $$

Answered by a.lgnaoui last updated on 19/Feb/23

△ABC et △ADE semblables ((AB)/(AD))=((AC)/(AE))=((BC)/(DE)) 1•((AB)/(AD))=((BC)/(DE)) ⇒AB=((BC×AD)/(DE)) AB=((2a)/b)BC △ACB BC∣∣DE ⇒∡DEC=∡BCA=2α AB^2 =AC^2 +BC^2 −2AC×BCcos 2α ((4a^2 )/b^2 )BC^2 =18^2 +BC^2 −36BCcos 2α (((4a^2 −b^2 )/b^2 ))BC^2 +36cos 2α)BC−18^2 =0 BC^2 +((b^2 ×36cos 2α))/(4a^2 −b^2 ))BC−((18^2 b^2 )/(4a^2 −b^2 ))=0 (BC+((18b^2 cos 2α)/(4a^2 −b^2 )))^2 −(((18^2 b^4 cos^2 2α+18^2 b^2 (4a^2 −b^2 ))/((4a^2 −b^2 )^2 )) =0 (BC+((18b^2 cos 2α)/(4a^2 −b^2 )))^2 −[((18^2 ×b^4 (4a^2 −sin^2 2α))/((4a^2 −b^2 )^2 ))]=0 BC+((18b^2 cos 2α)/(4a^2 −b^2 )) ±((18b^2 (√(4a^2 −sin^2 2α )))/(4a^2 −b^2 )) { ((BC=[((18b^2 )/(4a^2 −b^2 ))(cos 2α+(√(4a^2 −sin ^2 2α)) )])),((BC=[((18b^2 )/(4a^2 −b^2 ))(cos 2α−(√(4a^2 −sin ^2 2α)))])) :}

$$\bigtriangleup{ABC}\:\:\:{et}\:\bigtriangleup{ADE}\:{semblables} \\ $$$$\frac{{AB}}{{AD}}=\frac{{AC}}{{AE}}=\frac{{BC}}{{DE}} \\ $$$$\mathrm{1}\bullet\frac{{AB}}{{AD}}=\frac{{BC}}{{DE}}\:\:\:\:\:\Rightarrow{AB}=\frac{{BC}×{AD}}{{DE}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{AB}=\frac{\mathrm{2}{a}}{{b}}{BC} \\ $$$$\bigtriangleup{ACB}\:\:\:\:{BC}\mid\mid{DE}\:\:\Rightarrow\measuredangle{DEC}=\measuredangle{BCA}=\mathrm{2}\alpha \\ $$$$ \\ $$$$\:{AB}^{\mathrm{2}} ={AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} −\mathrm{2}{AC}×{BC}\mathrm{cos}\:\mathrm{2}\alpha \\ $$$$\frac{\mathrm{4}{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{BC}^{\mathrm{2}} =\mathrm{18}^{\mathrm{2}} +{BC}^{\mathrm{2}} −\mathrm{36}{BC}\mathrm{cos}\:\mathrm{2}\alpha \\ $$$$ \\ $$$$\left.\left(\frac{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right){BC}^{\mathrm{2}} +\mathrm{36cos}\:\mathrm{2}\alpha\right){BC}−\mathrm{18}^{\mathrm{2}} =\mathrm{0} \\ $$$${BC}^{\mathrm{2}} +\frac{\left.{b}^{\mathrm{2}} ×\mathrm{36cos}\:\mathrm{2}\alpha\right)}{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{BC}−\frac{\mathrm{18}^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left({BC}+\frac{\mathrm{18}{b}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} −\left(\frac{\mathrm{18}^{\mathrm{2}} {b}^{\mathrm{4}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\alpha+\mathrm{18}^{\mathrm{2}} {b}^{\mathrm{2}} \left(\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\left(\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\:\:=\mathrm{0}\right. \\ $$$$\left({BC}+\frac{\mathrm{18}{b}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} −\left[\frac{\mathrm{18}^{\mathrm{2}} ×{b}^{\mathrm{4}} \left(\mathrm{4}{a}^{\mathrm{2}} −\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\alpha\right)}{\left(\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\right]=\mathrm{0} \\ $$$$ \\ $$$${BC}+\frac{\mathrm{18}{b}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\:\pm\frac{\mathrm{18}{b}^{\mathrm{2}} \sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \mathrm{2}\alpha\:}}{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$ \\ $$$$\begin{cases}{{BC}=\left[\frac{\mathrm{18}{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\left(\mathrm{cos}\:\mathrm{2}\alpha+\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{sin}\:\:^{\mathrm{2}} \mathrm{2}\alpha}\:\right)\right]}\\{{BC}=\left[\frac{\mathrm{18}{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\left(\mathrm{cos}\:\mathrm{2}\alpha−\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{sin}\:\:^{\mathrm{2}} \mathrm{2}\alpha}\right)\right]}\end{cases}\: \\ $$

Commented by mr W last updated on 19/Feb/23

you seem not to understand the question correctly. a, b, α just mean that the corresponding line segments are equal and the corresponding angles are equal, they are not known values. the only value given is AC=18.

$${you}\:{seem}\:{not}\:{to}\:{understand}\:{the} \\ $$$${question}\:{correctly}.\:{a},\:{b},\:\alpha\:{just}\:{mean}\: \\ $$$${that}\:{the}\:{corresponding}\:{line}\:{segments} \\ $$$${are}\:{equal}\:{and}\:{the}\:{corresponding} \\ $$$${angles}\:{are}\:{equal},\:{they}\:{are}\:{not}\:{known} \\ $$$${values}.\:{the}\:{only}\:{value}\:{given}\:{is}\: \\ $$$${AC}=\mathrm{18}. \\ $$

Commented by a.lgnaoui last updated on 19/Feb/23

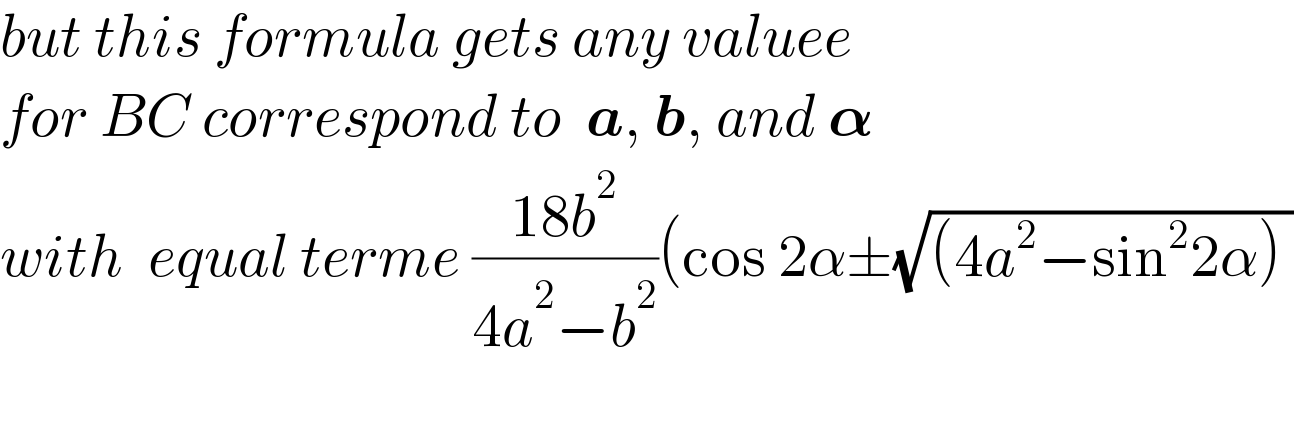
but this formula gets any valuee for BC correspond to a, b, and 𝛂 with equal terme ((18b^2 )/(4a^2 −b^2 ))(cos 2α±(√((4a^2 −sin^2 2α) ))

$${but}\:{this}\:{formula}\:{gets}\:{any}\:{valuee} \\ $$$${for}\:{BC}\:{correspond}\:{to}\:\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:{and}\:\boldsymbol{\alpha} \\ $$$${with}\:\:{equal}\:{terme}\:\frac{\mathrm{18}{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\left(\mathrm{cos}\:\mathrm{2}\alpha\pm\sqrt{\left(\mathrm{4}{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \mathrm{2}\alpha\right)\:}\right. \\ $$$$ \\ $$

Commented by mr W last updated on 19/Feb/23

but a,b and α can not be any values! they are not independent. they have actually fixed values through the value of AC=18.

$${but}\:{a},{b}\:{and}\:\alpha\:{can}\:{not}\:{be}\:{any}\:{values}!\: \\ $$$${they}\:{are}\:{not}\:{independent}.\:\:{they}\:{have} \\ $$$${actually}\:{fixed}\:{values}\:{through}\:{the} \\ $$$${value}\:{of}\:{AC}=\mathrm{18}. \\ $$

Answered by ajfour last updated on 19/Feb/23

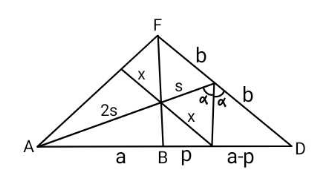
Commented by ajfour last updated on 19/Feb/23

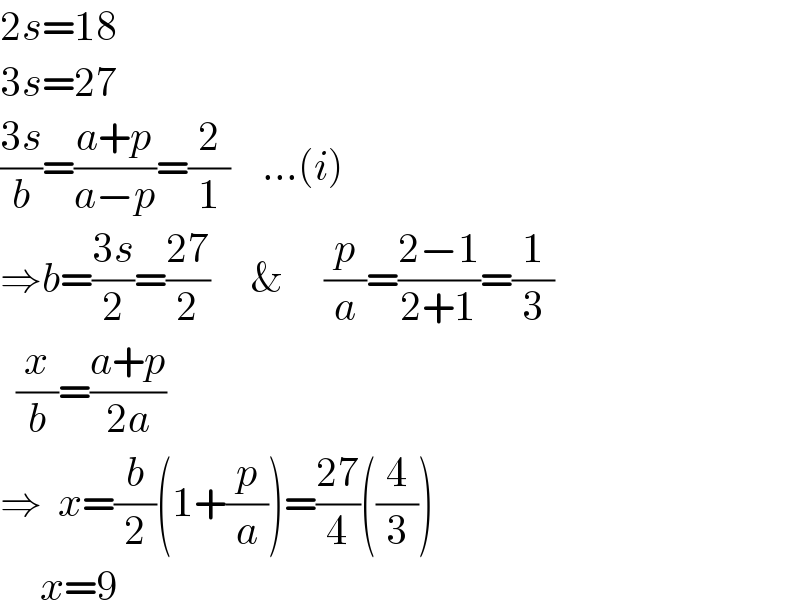
2s=18 3s=27 ((3s)/b)=((a+p)/(a−p))=(2/1) ...(i) ⇒b=((3s)/2)=((27)/2) & (p/a)=((2−1)/(2+1))=(1/3) (x/b)=((a+p)/(2a)) ⇒ x=(b/2)(1+(p/a))=((27)/4)((4/3)) x=9

$$\mathrm{2}{s}=\mathrm{18} \\ $$$$\mathrm{3}{s}=\mathrm{27} \\ $$$$\frac{\mathrm{3}{s}}{{b}}=\frac{{a}+{p}}{{a}−{p}}=\frac{\mathrm{2}}{\mathrm{1}}\:\:\:\:...\left({i}\right) \\ $$$$\Rightarrow{b}=\frac{\mathrm{3}{s}}{\mathrm{2}}=\frac{\mathrm{27}}{\mathrm{2}}\:\:\:\:\:\&\:\:\:\:\:\frac{{p}}{{a}}=\frac{\mathrm{2}−\mathrm{1}}{\mathrm{2}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:\frac{{x}}{{b}}=\frac{{a}+{p}}{\mathrm{2}{a}}\: \\ $$$$\Rightarrow\:\:{x}=\frac{{b}}{\mathrm{2}}\left(\mathrm{1}+\frac{{p}}{{a}}\right)=\frac{\mathrm{27}}{\mathrm{4}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:{x}=\mathrm{9} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com