Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 187535 by ajfour last updated on 18/Feb/23

Commented by ajfour last updated on 18/Feb/23

Q.187482

$${Q}.\mathrm{187482} \\ $$

Answered by ajfour last updated on 19/Feb/23

We alraedy have obtained, s=tan α=(R/H) pcos 30°=b ⇒ (p/b)=(2/( (√3))) ((bcos α+p)/(ccos α))=((AE)/(AGcos α))=((2(√(bc)))/(ccot α))+1 ⇒ (b/c)(1+(2/( (√3)cos α)))=(2/(cot α))(√(b/c))+1 say (b/c)=λ tan α=s, cos α=(1/( (√(1+s^2 )))) λ(1+((2(√(1+s^2 )))/( (√3))))−2s(√λ)−1=0 (1/λ)+((2s)/( (√λ)))−(1+((2(√(1+s^2 )))/( (√3))))=0 (1/( (√λ)))=(√(c/b))=−s+(√(s^2 +1+2(√((1+s^2 )/3)))) −−−−−−−−−−−−−−−− examples: for s=(1/( (√2))) ⇒ sin α=(1/( (√3))) (1/( (√λ)))=(√(c/b))=−(1/( (√2)))+(√((3/2)+(√2)))=1 for α=60° (1/( (√λ)))=−(√3)+(√(3+1+(4/( (√3))))) (√(c/b))=−(√3)+2(√(1+(1/( (√3))))) ≈ 0.7798 ⇒ b≈1.6445 for α=30° (√(c/b))=((2(√2)−1)/( (√3))) b≈0.8974

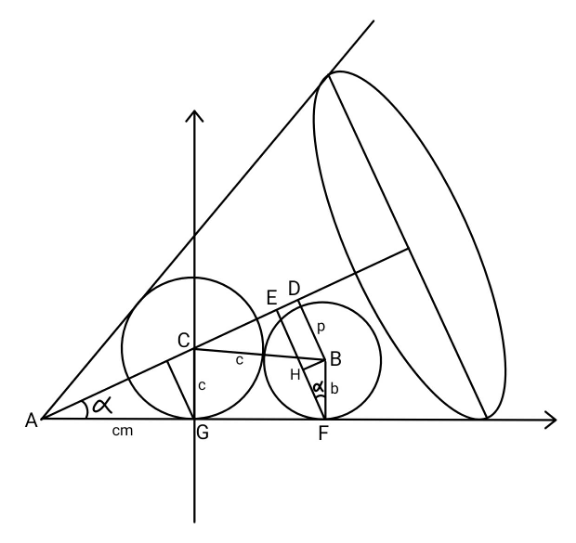
$${We}\:{alraedy}\:\:{have}\:{obtained}, \\ $$$${s}=\mathrm{tan}\:\alpha=\frac{{R}}{{H}} \\ $$$${p}\mathrm{cos}\:\mathrm{30}°={b}\:\:\:\Rightarrow\:\:\frac{{p}}{{b}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\frac{{b}\mathrm{cos}\:\alpha+{p}}{{c}\mathrm{cos}\:\alpha}=\frac{{AE}}{{AG}\mathrm{cos}\:\alpha}=\frac{\mathrm{2}\sqrt{{bc}}}{{c}\mathrm{cot}\:\alpha}+\mathrm{1} \\ $$$$\Rightarrow\:\:\frac{{b}}{{c}}\left(\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\mathrm{cos}\:\alpha}\right)=\frac{\mathrm{2}}{\mathrm{cot}\:\alpha}\sqrt{\frac{{b}}{{c}}}+\mathrm{1} \\ $$$${say}\:\frac{{b}}{{c}}=\lambda\:\:\:\mathrm{tan}\:\alpha={s},\:\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{s}^{\mathrm{2}} }} \\ $$$$\lambda\left(\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{1}+{s}^{\mathrm{2}} }}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{2}{s}\sqrt{\lambda}−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\lambda}+\frac{\mathrm{2}{s}}{\:\sqrt{\lambda}}−\left(\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{1}+{s}^{\mathrm{2}} }}{\:\sqrt{\mathrm{3}}}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\lambda}}=\sqrt{\frac{{c}}{{b}}}=−{s}+\sqrt{{s}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}\sqrt{\frac{\mathrm{1}+{s}^{\mathrm{2}} }{\mathrm{3}}}} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${examples}: \\ $$$${for}\:\:\:{s}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:\:\Rightarrow\:\:\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\lambda}}=\sqrt{\frac{{c}}{{b}}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}+\sqrt{\mathrm{2}}}=\mathrm{1} \\ $$$${for}\:\alpha=\mathrm{60}° \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\lambda}}=−\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}+\mathrm{1}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}} \\ $$$$\:\:\:\:\sqrt{\frac{{c}}{{b}}}=−\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\:\mathrm{0}.\mathrm{7798} \\ $$$$\Rightarrow\:\:\:{b}\approx\mathrm{1}.\mathrm{6445} \\ $$$${for}\:\:\alpha=\mathrm{30}° \\ $$$$\:\:\:\:\:\:\sqrt{\frac{{c}}{{b}}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:{b}\approx\mathrm{0}.\mathrm{8974} \\ $$

Commented by ajfour last updated on 19/Feb/23

Thanks Sir, edited.

$${Thanks}\:{Sir},\:{edited}. \\ $$

Commented by mr W last updated on 19/Feb/23

perfect solution sir!

$${perfect}\:{solution}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com