
Question Number 187482 by ajfour last updated on 17/Feb/23

Commented by ajfour last updated on 17/Feb/23

$${If}\:\:\:\:{cone}'{s}\:\:\:\:\:\frac{{R}}{{h}}={m},\:\:{green}\:{ball} \\ $$$${radius}={a}.\:\:{Find}\:{b}\:{the}\:{radii}\:{of} \\ $$$${upper}\:{balls}\:\left({equal}\right),\:{all}\:{in}\:{contact} \\ $$$${the}\:{way}\:{shown}. \\ $$
Answered by a.lgnaoui last updated on 18/Feb/23
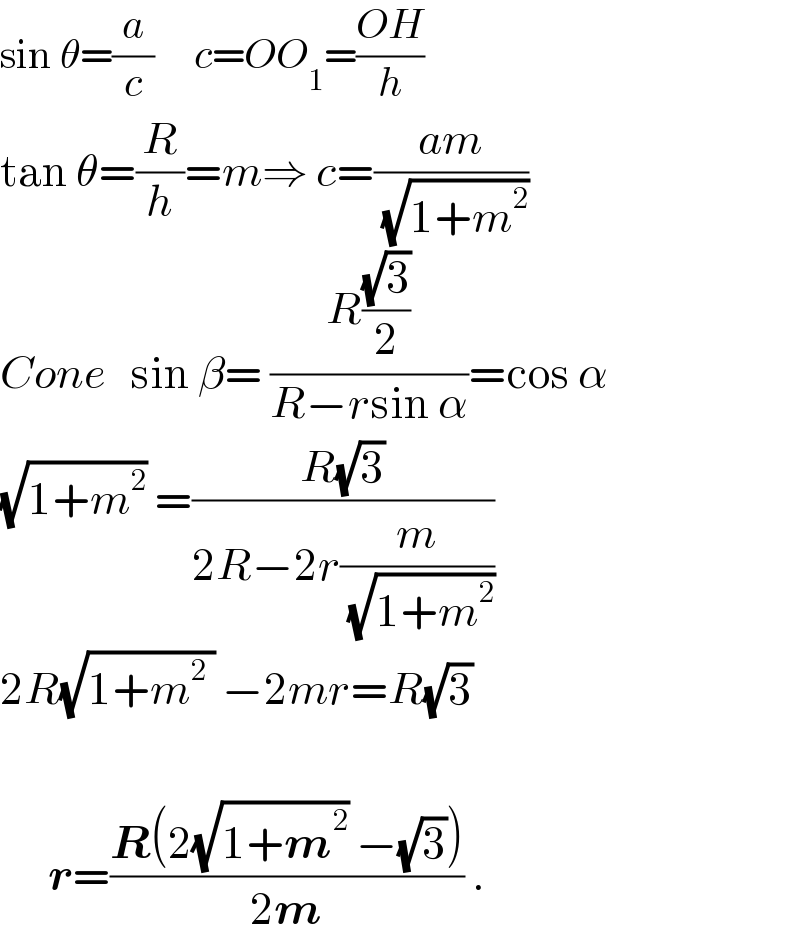
$$\mathrm{sin}\:\theta=\frac{{a}}{{c}}\:\:\:\:\:{c}={OO}_{\mathrm{1}} =\frac{{OH}}{{h}} \\ $$$$\mathrm{tan}\:\theta=\frac{{R}}{{h}}={m}\Rightarrow\:{c}=\frac{{am}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }} \\ $$$${Cone}\:\:\:\mathrm{sin}\:\beta=\:\frac{{R}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{{R}−{r}\mathrm{sin}\:\alpha}=\mathrm{cos}\:\alpha \\ $$$$\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\:=\frac{{R}\sqrt{\mathrm{3}}}{\mathrm{2}{R}−\mathrm{2}{r}\frac{{m}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}} \\ $$$$\mathrm{2}{R}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} \:}\:−\mathrm{2}{mr}={R}\sqrt{\mathrm{3}}\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\boldsymbol{{r}}=\frac{\boldsymbol{{R}}\left(\mathrm{2}\sqrt{\mathrm{1}+\boldsymbol{{m}}^{\mathrm{2}} }\:−\sqrt{\mathrm{3}}\right)}{\mathrm{2}\boldsymbol{{m}}}\:. \\ $$
Commented by a.lgnaoui last updated on 18/Feb/23

$${r}={b} \\ $$
Commented by a.lgnaoui last updated on 18/Feb/23
Answered by mr W last updated on 18/Feb/23

Commented by mr W last updated on 19/Feb/23

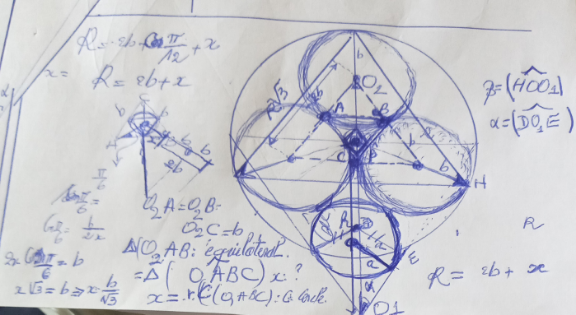
$$\mathrm{tan}\:\theta=\frac{{R}}{{H}}={m} \\ $$$${A}'{B}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{b}}{\mathrm{3}} \\ $$$${OA}=\frac{{a}}{\mathrm{sin}\:\theta} \\ $$$${AA}'=\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}{b}}{\mathrm{3}}\right)^{\mathrm{2}} }=\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{ab}−\frac{{b}^{\mathrm{2}} }{\mathrm{3}}} \\ $$$${OA}'=\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{ab}−\frac{{b}^{\mathrm{2}} }{\mathrm{3}}}+\frac{{a}}{\mathrm{sin}\:\theta} \\ $$$${OC}=\frac{{a}}{\mathrm{tan}\:\theta} \\ $$$${CC}'=\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left({b}−{a}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{ab}} \\ $$$${OC}'=\mathrm{2}\sqrt{{ab}}+\frac{{a}}{\mathrm{tan}\:\theta} \\ $$$$\left(\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{ab}−\frac{{b}^{\mathrm{2}} }{\mathrm{3}}}+\frac{{a}}{\mathrm{sin}\:\theta}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}{b}}{\mathrm{3}}\right)^{\mathrm{2}} =\left(\mathrm{2}\sqrt{{ab}}+\frac{{a}}{\mathrm{tan}\:\theta}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{ab}−\frac{{b}^{\mathrm{2}} }{\mathrm{3}}}=\left({b}−{a}\right)\mathrm{sin}\:\theta+\mathrm{2}\sqrt{{ab}}\:\mathrm{cos}\:\theta \\ $$$${b}^{\mathrm{2}} \left(\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)−{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}{ab}\left(\mathrm{2}−\mathrm{3cos}^{\mathrm{2}} \:\theta\right)+\mathrm{2}\left({b}−{a}\right)\sqrt{{ab}}\:\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0} \\ $$$${let}\:\lambda=\frac{{b}}{{a}} \\ $$$$\Rightarrow\left(\mathrm{5}−\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\theta\right)\lambda^{\mathrm{2}} −\mathrm{6}\left(\mathrm{1}−\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\theta\right)\lambda+\mathrm{12}\:\mathrm{sin}\:\mathrm{2}\theta\:\left(\lambda−\mathrm{1}\right)\sqrt{\lambda}−\mathrm{3}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)=\mathrm{0} \\ $$$$ \\ $$$${examples}: \\ $$$$\theta=\mathrm{30}°\:\Rightarrow\frac{{b}}{{a}}\approx\mathrm{0}.\mathrm{8974} \\ $$$$\theta=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\approx\mathrm{35}.\mathrm{264}°\:\Rightarrow\frac{{b}}{{a}}=\mathrm{1} \\ $$$$\theta=\mathrm{60}°\:\Rightarrow\frac{{b}}{{a}}\approx\mathrm{1}.\mathrm{6445} \\ $$
Commented by a.lgnaoui last updated on 18/Feb/23
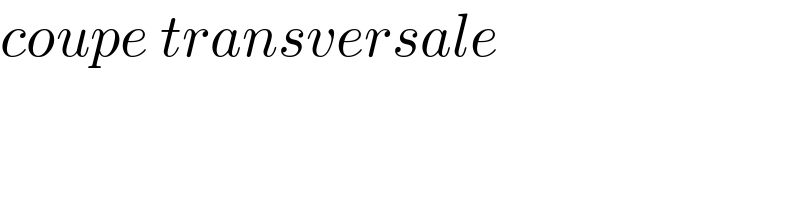
$${coupe}\:{transversale} \\ $$
Commented by ajfour last updated on 19/Feb/23
Thanks Sir , correct answers.
Answered by ajfour last updated on 18/Feb/23

Commented by ajfour last updated on 18/Feb/23
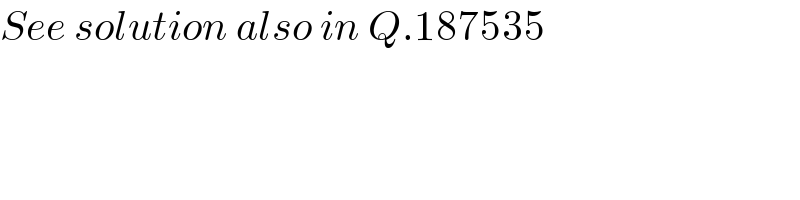
$${See}\:{solution}\:{also}\:{in}\:{Q}.\mathrm{187535} \\ $$
Commented by a.lgnaoui last updated on 18/Feb/23

$${Merci}\:{pour}\:{explication}\:{par} \\ $$$${graphe}. \\ $$
