
Question Number 18746 by khamizan833@yahoo.com last updated on 29/Jul/17
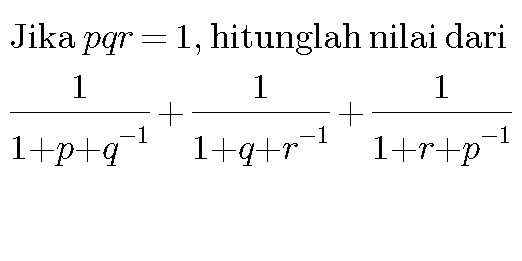
Answered by daffa22 last updated on 30/Jul/17
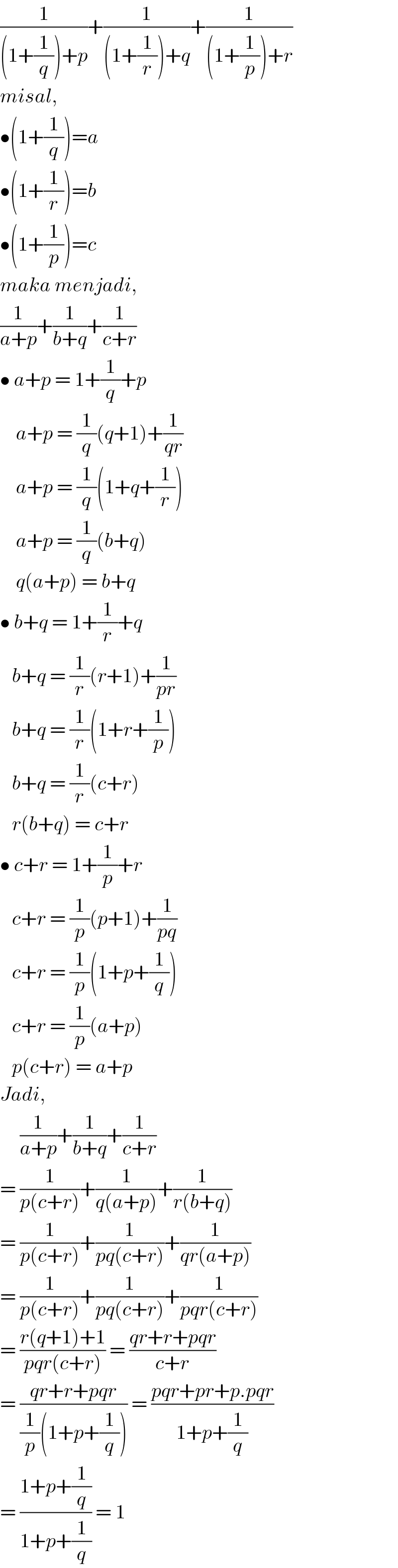
$$\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{q}}\right)+{p}}+\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{r}}\right)+{q}}+\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{p}}\right)+{r}} \\ $$$${misal}, \\ $$$$\bullet\left(\mathrm{1}+\frac{\mathrm{1}}{{q}}\right)={a} \\ $$$$\bullet\left(\mathrm{1}+\frac{\mathrm{1}}{{r}}\right)={b} \\ $$$$\bullet\left(\mathrm{1}+\frac{\mathrm{1}}{{p}}\right)={c} \\ $$$${maka}\:{menjadi}, \\ $$$$\frac{\mathrm{1}}{{a}+{p}}+\frac{\mathrm{1}}{{b}+{q}}+\frac{\mathrm{1}}{{c}+{r}} \\ $$$$\bullet\:{a}+{p}\:=\:\mathrm{1}+\frac{\mathrm{1}}{{q}}+{p} \\ $$$$\:\:\:\:{a}+{p}\:=\:\frac{\mathrm{1}}{{q}}\left({q}+\mathrm{1}\right)+\frac{\mathrm{1}}{{qr}} \\ $$$$\:\:\:\:{a}+{p}\:=\:\frac{\mathrm{1}}{{q}}\left(\mathrm{1}+{q}+\frac{\mathrm{1}}{{r}}\right) \\ $$$$\:\:\:\:{a}+{p}\:=\:\frac{\mathrm{1}}{{q}}\left({b}+{q}\right) \\ $$$$\:\:\:\:{q}\left({a}+{p}\right)\:=\:{b}+{q} \\ $$$$\bullet\:{b}+{q}\:=\:\mathrm{1}+\frac{\mathrm{1}}{{r}}+{q} \\ $$$$\:\:\:{b}+{q}\:=\:\frac{\mathrm{1}}{{r}}\left({r}+\mathrm{1}\right)+\frac{\mathrm{1}}{{pr}} \\ $$$$\:\:\:{b}+{q}\:=\:\frac{\mathrm{1}}{{r}}\left(\mathrm{1}+{r}+\frac{\mathrm{1}}{{p}}\right) \\ $$$$\:\:\:{b}+{q}\:=\:\frac{\mathrm{1}}{{r}}\left({c}+{r}\right) \\ $$$$\:\:\:{r}\left({b}+{q}\right)\:=\:{c}+{r} \\ $$$$\bullet\:{c}+{r}\:=\:\mathrm{1}+\frac{\mathrm{1}}{{p}}+{r} \\ $$$$\:\:\:{c}+{r}\:=\:\frac{\mathrm{1}}{{p}}\left({p}+\mathrm{1}\right)+\frac{\mathrm{1}}{{pq}} \\ $$$$\:\:\:{c}+{r}\:=\:\frac{\mathrm{1}}{{p}}\left(\mathrm{1}+{p}+\frac{\mathrm{1}}{{q}}\right) \\ $$$$\:\:\:{c}+{r}\:=\:\frac{\mathrm{1}}{{p}}\left({a}+{p}\right) \\ $$$$\:\:\:{p}\left({c}+{r}\right)\:=\:{a}+{p} \\ $$$${Jadi}, \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{{a}+{p}}+\frac{\mathrm{1}}{{b}+{q}}+\frac{\mathrm{1}}{{c}+{r}} \\ $$$$=\:\frac{\mathrm{1}}{{p}\left({c}+{r}\right)}+\frac{\mathrm{1}}{{q}\left({a}+{p}\right)}+\frac{\mathrm{1}}{{r}\left({b}+{q}\right)} \\ $$$$=\:\frac{\mathrm{1}}{{p}\left({c}+{r}\right)}+\frac{\mathrm{1}}{{pq}\left({c}+{r}\right)}+\frac{\mathrm{1}}{{qr}\left({a}+{p}\right)} \\ $$$$=\:\frac{\mathrm{1}}{{p}\left({c}+{r}\right)}+\frac{\mathrm{1}}{{pq}\left({c}+{r}\right)}+\frac{\mathrm{1}}{{pqr}\left({c}+{r}\right)} \\ $$$$=\:\frac{{r}\left({q}+\mathrm{1}\right)+\mathrm{1}}{{pqr}\left({c}+{r}\right)}\:=\:\frac{{qr}+{r}+{pqr}}{{c}+{r}} \\ $$$$=\:\frac{{qr}+{r}+{pqr}}{\frac{\mathrm{1}}{{p}}\left(\mathrm{1}+{p}+\frac{\mathrm{1}}{{q}}\right)}\:=\:\frac{{pqr}+{pr}+{p}.{pqr}}{\mathrm{1}+{p}+\frac{\mathrm{1}}{{q}}} \\ $$$$=\:\frac{\mathrm{1}+{p}+\frac{\mathrm{1}}{{q}}}{\mathrm{1}+{p}+\frac{\mathrm{1}}{{q}}}\:=\:\mathrm{1} \\ $$
Answered by behi.8.3.4.1.7@gmail.com last updated on 30/Jul/17

$${LHS}=\frac{{q}}{\mathrm{1}+{q}+{pq}}+\frac{{r}}{\mathrm{1}+{r}+{rq}}+\frac{{p}}{\mathrm{1}+{p}+{pr}}= \\ $$$$=\frac{{q}}{{pqr}+{q}+{pq}}+\frac{{rp}}{{p}+{rp}+\mathrm{1}}+\frac{{p}}{\mathrm{1}+{p}+{pr}}= \\ $$$$=\frac{\mathrm{1}}{{p}+{pr}+\mathrm{1}}+\frac{{pr}}{\mathrm{1}+{rp}+\mathrm{1}}+\frac{{p}}{\mathrm{1}+{p}+{pr}}= \\ $$$$=\frac{\mathrm{1}+{pr}+{p}}{\mathrm{1}+{pr}+{p}}=\mathrm{1}\:.\blacksquare \\ $$
