
Question Number 187394 by Rupesh123 last updated on 16/Feb/23
Commented by Rupesh123 last updated on 16/Feb/23
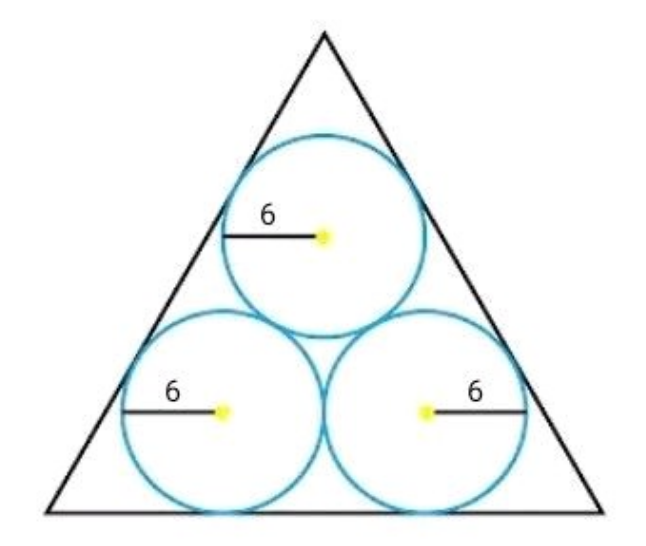
Area of equilateral triangle?
Answered by HeferH last updated on 16/Feb/23
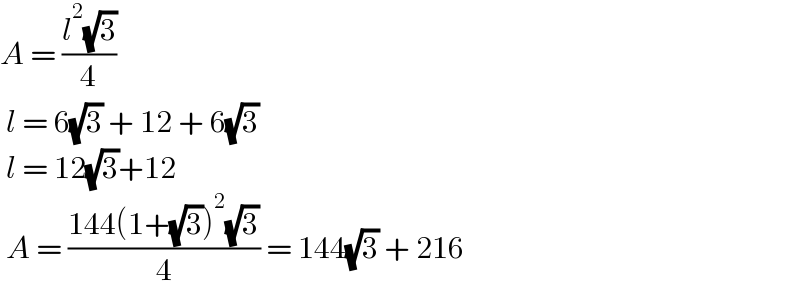
$${A}\:=\:\frac{{l}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\:{l}\:=\:\mathrm{6}\sqrt{\mathrm{3}}\:+\:\mathrm{12}\:+\:\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$\:{l}\:=\:\mathrm{12}\sqrt{\mathrm{3}}+\mathrm{12} \\ $$$$\:{A}\:=\:\frac{\mathrm{144}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}\:=\:\mathrm{144}\sqrt{\mathrm{3}}\:+\:\mathrm{216} \\ $$
Commented by Rupesh123 last updated on 16/Feb/23
Good!
