
Question Number 187186 by 073 last updated on 14/Feb/23
Commented by 073 last updated on 14/Feb/23

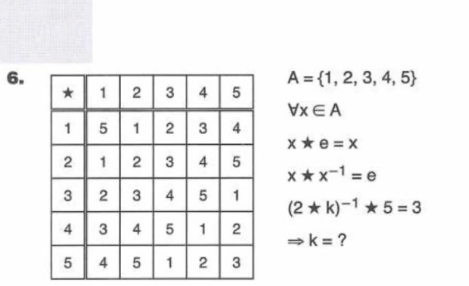
$$\mathrm{please}\:\mathrm{solution}?? \\ $$
Commented by Rasheed.Sindhi last updated on 15/Feb/23

$$\mathrm{k}=\mathrm{4}\:\left(\mathrm{please}\:\mathrm{confirm}\:\mathrm{the}\:\mathrm{answer}\right) \\ $$
Commented by mr W last updated on 15/Feb/23

$${k}=\mathrm{4}\:{is}\:{correct}. \\ $$
Commented by Rasheed.Sindhi last updated on 16/Feb/23
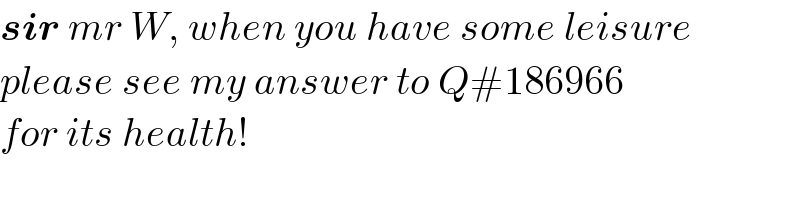
$$\boldsymbol{{sir}}\:{mr}\:{W},\:{when}\:{you}\:{have}\:{some}\:{leisure} \\ $$$${please}\:{see}\:{my}\:{answer}\:{to}\:{Q}#\mathrm{186966} \\ $$$${for}\:{its}\:{health}! \\ $$
Commented by 073 last updated on 16/Feb/23

$$\mathrm{thanks} \\ $$
Commented by 073 last updated on 16/Feb/23

$$\mathrm{thanks} \\ $$
Answered by Rasheed.Sindhi last updated on 15/Feb/23
![determinant ((★,1,2,3,4,5),(1,5,1,2,3,4),(2,1,2,3,4,5),(3,2,3,4,5,1),(4,3,4,5,1,2),(5,4,5,1,2,3)) A={1,2,3,4,5} x★e=x ∀x∈A⇒e=2 1^(−1) =3 [∵ 1★3=2] 2^(−1) =2 [∵ 2★2=2] 3^(−1) =1 [∵ 3★1=2] 4^(−1) =5 [∵ 4★5=2] 5^(−1) =4 [∵ 5★4=2] (2★k)^(−1) ★5=3 k^(−1) ★5=3 [∵2★k=k] k^(−1) ★5★5^(−1) =3★5^(−1) k^(−1) ★(5★5^(−1) )=3★4 [∵5^(−1) =4] k^(−1) ★2=3★4 [∵5★5^(−1) =2] k^(−1) =5 [∵ k^(−1) ★2=k^(−1) ] k=4](Q187290.png)
$$\begin{array}{|c|c|c|c|c|c|}{\bigstar}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}\\{\mathrm{1}}&\hline{\mathrm{5}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}\\{\mathrm{2}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}\\{\mathrm{3}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{1}}\\{\mathrm{4}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}\\{\mathrm{5}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}\\\hline\end{array} \\ $$$$\mathrm{A}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right\} \\ $$$$\mathrm{x}\bigstar\mathrm{e}=\mathrm{x}\:\forall\mathrm{x}\in\mathrm{A}\Rightarrow\mathrm{e}=\mathrm{2} \\ $$$$\mathrm{1}^{−\mathrm{1}} =\mathrm{3}\:\:\:\left[\because\:\mathrm{1}\bigstar\mathrm{3}=\mathrm{2}\right] \\ $$$$\mathrm{2}^{−\mathrm{1}} =\mathrm{2}\:\:\:\left[\because\:\mathrm{2}\bigstar\mathrm{2}=\mathrm{2}\right] \\ $$$$\mathrm{3}^{−\mathrm{1}} =\mathrm{1}\:\:\:\:\left[\because\:\mathrm{3}\bigstar\mathrm{1}=\mathrm{2}\right] \\ $$$$\mathrm{4}^{−\mathrm{1}} =\mathrm{5}\:\:\:\:\left[\because\:\mathrm{4}\bigstar\mathrm{5}=\mathrm{2}\right] \\ $$$$\mathrm{5}^{−\mathrm{1}} =\mathrm{4}\:\:\:\left[\because\:\mathrm{5}\bigstar\mathrm{4}=\mathrm{2}\right] \\ $$$$ \\ $$$$\left(\mathrm{2}\bigstar\mathrm{k}\right)^{−\mathrm{1}} \bigstar\mathrm{5}=\mathrm{3} \\ $$$$\mathrm{k}^{−\mathrm{1}} \bigstar\mathrm{5}=\mathrm{3}\:\:\:\left[\because\mathrm{2}\bigstar\mathrm{k}=\mathrm{k}\right] \\ $$$$\mathrm{k}^{−\mathrm{1}} \bigstar\mathrm{5}\bigstar\mathrm{5}^{−\mathrm{1}} =\mathrm{3}\bigstar\mathrm{5}^{−\mathrm{1}} \\ $$$$\mathrm{k}^{−\mathrm{1}} \bigstar\left(\mathrm{5}\bigstar\mathrm{5}^{−\mathrm{1}} \right)=\mathrm{3}\bigstar\mathrm{4}\:\:\left[\because\mathrm{5}^{−\mathrm{1}} =\mathrm{4}\right] \\ $$$$\mathrm{k}^{−\mathrm{1}} \bigstar\mathrm{2}=\mathrm{3}\bigstar\mathrm{4}\:\:\:\:\:\left[\because\mathrm{5}\bigstar\mathrm{5}^{−\mathrm{1}} =\mathrm{2}\right] \\ $$$$\mathrm{k}^{−\mathrm{1}} =\mathrm{5}\:\:\:\:\:\left[\because\:\mathrm{k}^{−\mathrm{1}} \bigstar\mathrm{2}=\mathrm{k}^{−\mathrm{1}} \right] \\ $$$$\mathrm{k}=\mathrm{4} \\ $$
Commented by 073 last updated on 16/Feb/23

$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 15/Feb/23
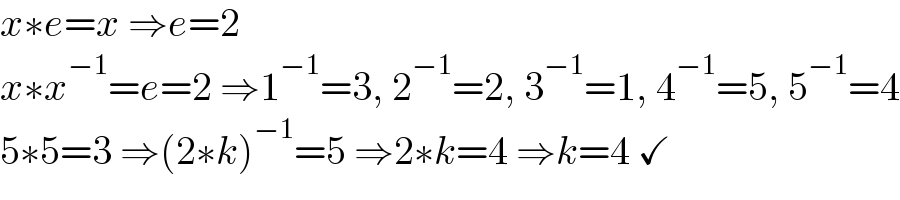
$${x}\ast{e}={x}\:\Rightarrow{e}=\mathrm{2} \\ $$$${x}\ast{x}^{−\mathrm{1}} ={e}=\mathrm{2}\:\Rightarrow\mathrm{1}^{−\mathrm{1}} =\mathrm{3},\:\mathrm{2}^{−\mathrm{1}} =\mathrm{2},\:\mathrm{3}^{−\mathrm{1}} =\mathrm{1},\:\mathrm{4}^{−\mathrm{1}} =\mathrm{5},\:\mathrm{5}^{−\mathrm{1}} =\mathrm{4} \\ $$$$\mathrm{5}\ast\mathrm{5}=\mathrm{3}\:\Rightarrow\left(\mathrm{2}\ast{k}\right)^{−\mathrm{1}} =\mathrm{5}\:\Rightarrow\mathrm{2}\ast{k}=\mathrm{4}\:\Rightarrow{k}=\mathrm{4}\:\checkmark \\ $$
Commented by 073 last updated on 16/Feb/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$
