Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 187167 by Rupesh123 last updated on 14/Feb/23

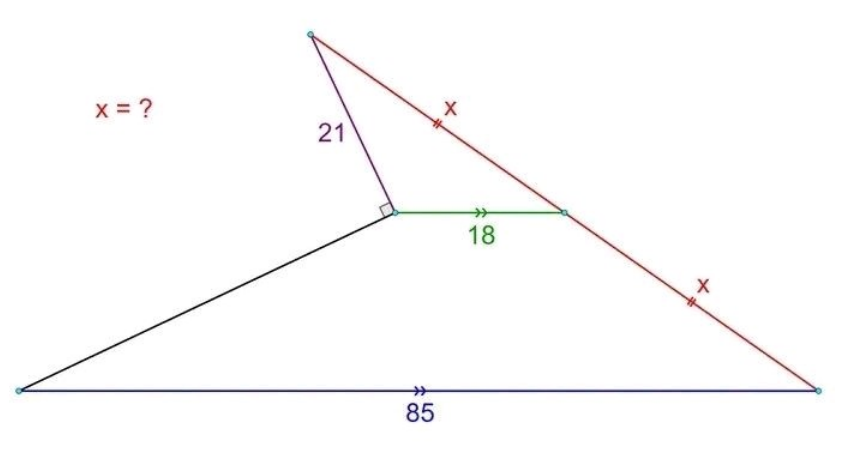
Answered by mr W last updated on 14/Feb/23

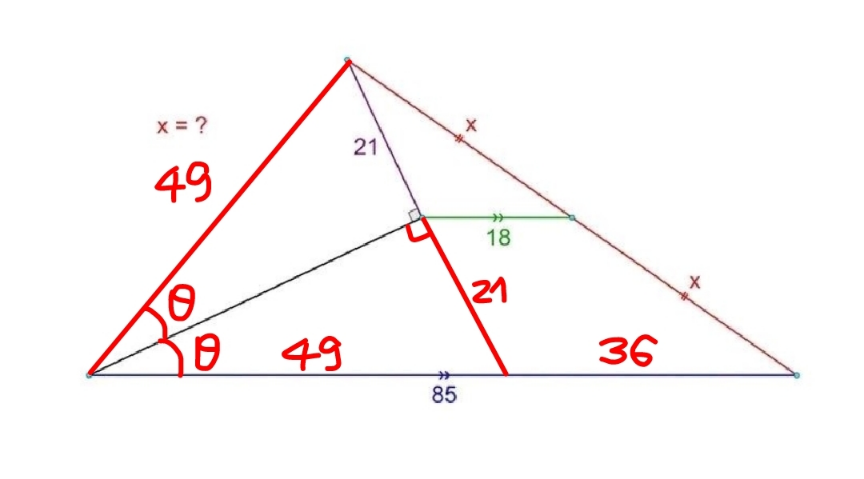
Commented by mr W last updated on 14/Feb/23

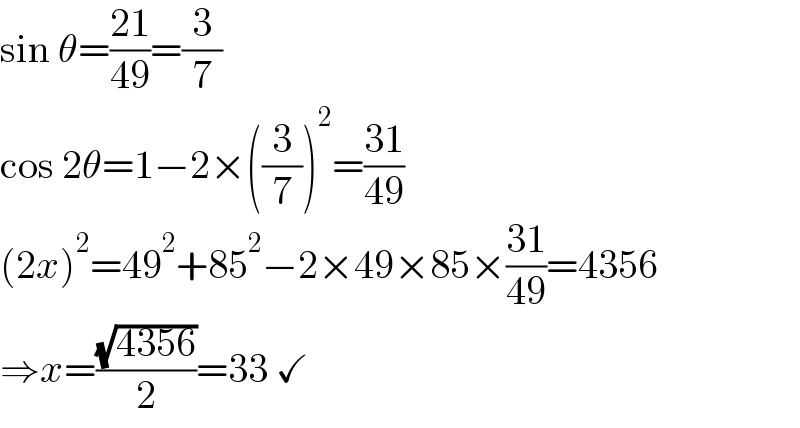
sin θ=((21)/(49))=(3/7) cos 2θ=1−2×((3/7))^2 =((31)/(49)) (2x)^2 =49^2 +85^2 −2×49×85×((31)/(49))=4356 ⇒x=((√(4356))/2)=33 ✓

$$\mathrm{sin}\:\theta=\frac{\mathrm{21}}{\mathrm{49}}=\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\mathrm{1}−\mathrm{2}×\left(\frac{\mathrm{3}}{\mathrm{7}}\right)^{\mathrm{2}} =\frac{\mathrm{31}}{\mathrm{49}} \\ $$$$\left(\mathrm{2}{x}\right)^{\mathrm{2}} =\mathrm{49}^{\mathrm{2}} +\mathrm{85}^{\mathrm{2}} −\mathrm{2}×\mathrm{49}×\mathrm{85}×\frac{\mathrm{31}}{\mathrm{49}}=\mathrm{4356} \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{4356}}}{\mathrm{2}}=\mathrm{33}\:\checkmark \\ $$

Commented by Rupesh123 last updated on 14/Feb/23

Nice!

Answered by mr W last updated on 14/Feb/23

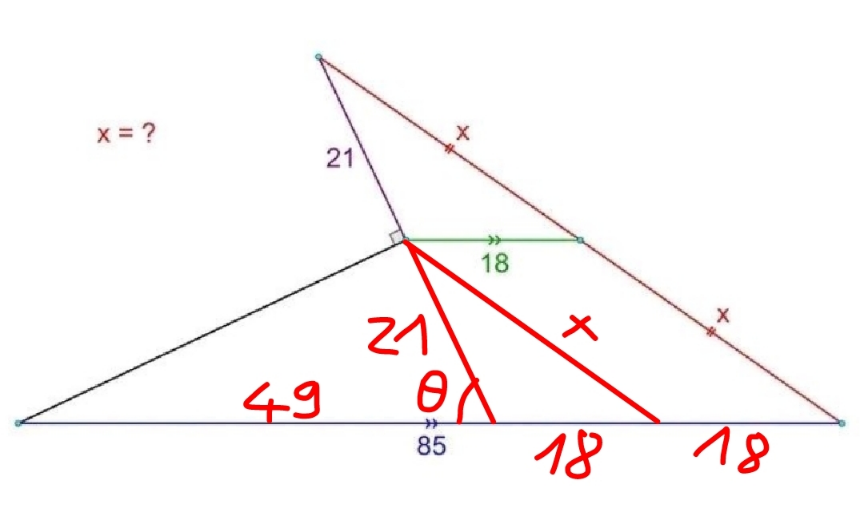
Commented by mr W last updated on 14/Feb/23

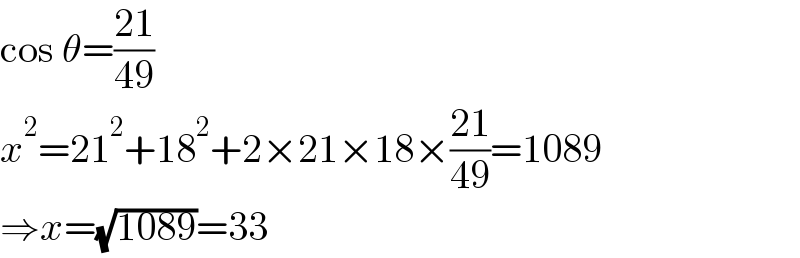
cos θ=((21)/(49)) x^2 =21^2 +18^2 +2×21×18×((21)/(49))=1089 ⇒x=(√(1089))=33

$$\mathrm{cos}\:\theta=\frac{\mathrm{21}}{\mathrm{49}} \\ $$$${x}^{\mathrm{2}} =\mathrm{21}^{\mathrm{2}} +\mathrm{18}^{\mathrm{2}} +\mathrm{2}×\mathrm{21}×\mathrm{18}×\frac{\mathrm{21}}{\mathrm{49}}=\mathrm{1089} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{1089}}=\mathrm{33} \\ $$

Commented by Rupesh123 last updated on 15/Feb/23

Good job!

Answered by a.lgnaoui last updated on 14/Feb/23

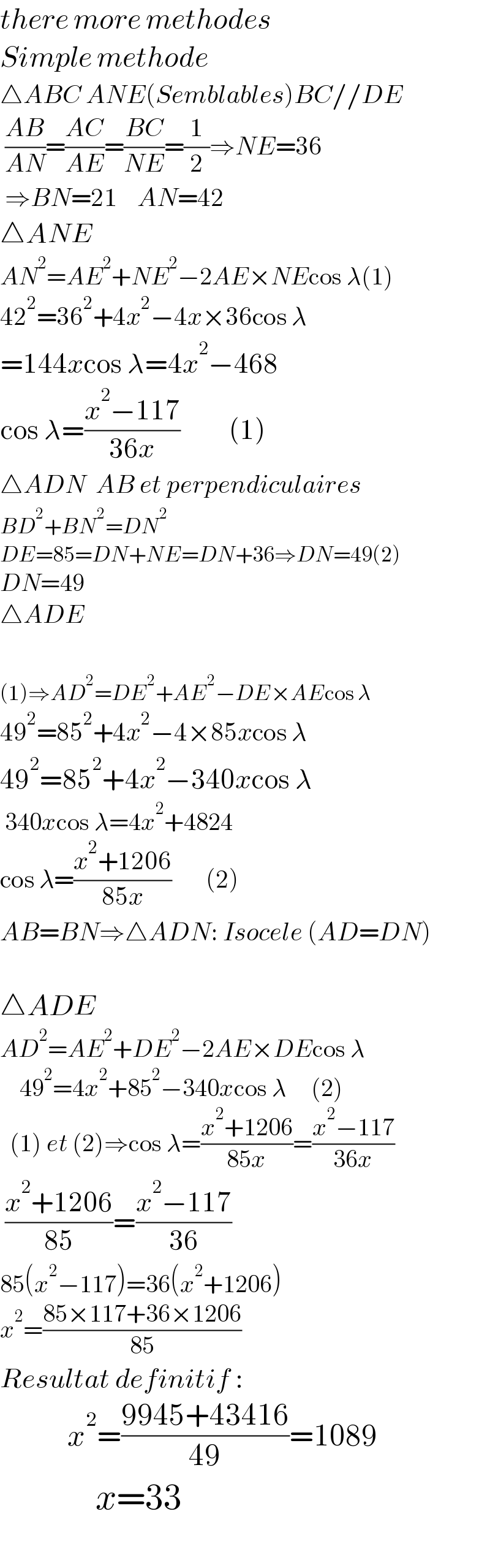
there more methodes Simple methode △ABC ANE(Semblables)BC//DE ((AB)/(AN))=((AC)/(AE))=((BC)/(NE))=(1/2)⇒NE=36 ⇒BN=21 AN=42 △ANE AN^2 =AE^2 +NE^2 −2AE×NEcos λ(1) 42^2 =36^2 +4x^2 −4x×36cos λ =144xcos λ=4x^2 −468 cos λ=((x^2 −117)/(36x)) (1) △ADN AB et perpendiculaires BD^2 +BN^2 =DN^2 DE=85=DN+NE=DN+36⇒DN=49(2) DN=49 △ADE (1)⇒AD^2 =DE^2 +AE^2 −DE×AEcos λ 49^2 =85^2 +4x^2 −4×85xcos λ 49^2 =85^2 +4x^2 −340xcos λ 340xcos λ=4x^2 +4824 cos λ=((x^2 +1206)/(85x)) (2) AB=BN⇒△ADN: Isocele (AD=DN) △ADE AD^2 =AE^2 +DE^2 −2AE×DEcos λ 49^2 =4x^2 +85^2 −340xcos λ (2) (1) et (2)⇒cos λ=((x^2 +1206)/(85x))=((x^2 −117)/(36x)) ((x^2 +1206)/(85))=((x^2 −117)/(36)) 85(x^2 −117)=36(x^2 +1206) x^2 =((85×117+36×1206)/(85)) Resultat definitif : x^2 =((9945+43416)/(49))=1089 x=33

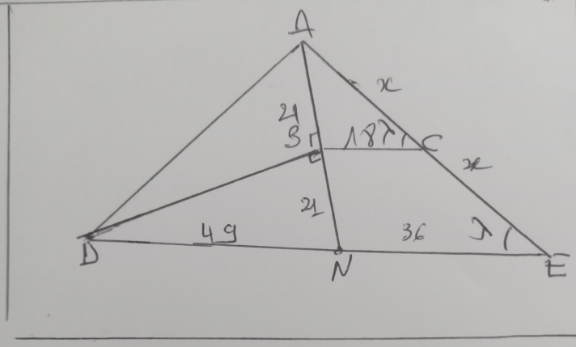
$${there}\:{more}\:{methodes} \\ $$$${Simple}\:{methode} \\ $$$$\bigtriangleup{ABC}\:{ANE}\left({Semblables}\right){BC}//{DE} \\ $$$$\:\frac{{AB}}{{AN}}=\frac{{AC}}{{AE}}=\frac{{BC}}{{NE}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{NE}=\mathrm{36} \\ $$$$\:\:\Rightarrow{BN}=\mathrm{21}\:\:\:\:{AN}=\mathrm{42} \\ $$$$\bigtriangleup{ANE}\:\: \\ $$$${AN}^{\mathrm{2}} ={AE}^{\mathrm{2}} +{NE}^{\mathrm{2}} −\mathrm{2}{AE}×{NE}\mathrm{cos}\:\lambda\left(\mathrm{1}\right) \\ $$$$\mathrm{42}^{\mathrm{2}} =\mathrm{36}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}×\mathrm{36cos}\:\lambda \\ $$$$=\mathrm{144}{x}\mathrm{cos}\:\lambda=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{468} \\ $$$$\mathrm{cos}\:\lambda=\frac{{x}^{\mathrm{2}} −\mathrm{117}}{\mathrm{36}{x}}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup{ADN}\:\:{AB}\:{et}\:{perpendiculaires} \\ $$$${BD}^{\mathrm{2}} +{BN}^{\mathrm{2}} ={DN}^{\mathrm{2}} \\ $$$${DE}=\mathrm{85}={DN}+{NE}={DN}+\mathrm{36}\Rightarrow{DN}=\mathrm{49}\left(\mathrm{2}\right) \\ $$$${DN}=\mathrm{49} \\ $$$$\bigtriangleup{ADE} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\Rightarrow{AD}^{\mathrm{2}} ={DE}^{\mathrm{2}} +{AE}^{\mathrm{2}} −{DE}×{AE}\mathrm{cos}\:\lambda \\ $$$$\mathrm{49}^{\mathrm{2}} =\mathrm{85}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}×\mathrm{85}{x}\mathrm{cos}\:\lambda \\ $$$$\mathrm{49}^{\mathrm{2}} =\mathrm{85}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{340}{x}\mathrm{cos}\:\lambda \\ $$$$\:\mathrm{340}{x}\mathrm{cos}\:\lambda=\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4824} \\ $$$$\mathrm{cos}\:\lambda=\frac{{x}^{\mathrm{2}} +\mathrm{1206}}{\mathrm{85}{x}}\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${AB}={BN}\Rightarrow\bigtriangleup{ADN}:\:{Isocele}\:\left({AD}={DN}\right) \\ $$$$ \\ $$$$\bigtriangleup{ADE}\:\:\: \\ $$$${AD}^{\mathrm{2}} ={AE}^{\mathrm{2}} +{DE}^{\mathrm{2}} −\mathrm{2}{AE}×{DE}\mathrm{cos}\:\lambda \\ $$$$\:\:\:\:\mathrm{49}^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} +\mathrm{85}^{\mathrm{2}} −\mathrm{340}{x}\mathrm{cos}\:\lambda\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\:\:\left(\mathrm{1}\right)\:{et}\:\left(\mathrm{2}\right)\Rightarrow\mathrm{cos}\:\lambda=\frac{{x}^{\mathrm{2}} +\mathrm{1206}}{\mathrm{85}{x}}=\frac{{x}^{\mathrm{2}} −\mathrm{117}}{\mathrm{36}{x}} \\ $$$$\:\frac{{x}^{\mathrm{2}} +\mathrm{1206}}{\mathrm{85}}=\frac{{x}^{\mathrm{2}} −\mathrm{117}}{\mathrm{36}} \\ $$$$\mathrm{85}\left({x}^{\mathrm{2}} −\mathrm{117}\right)=\mathrm{36}\left({x}^{\mathrm{2}} +\mathrm{1206}\right) \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{85}×\mathrm{117}+\mathrm{36}×\mathrm{1206}}{\mathrm{85}} \\ $$$${Resultat}\:{definitif}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\frac{\mathrm{9945}+\mathrm{43416}}{\mathrm{49}}=\mathrm{1089} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{33} \\ $$$$\: \\ $$

Commented by a.lgnaoui last updated on 14/Feb/23

Commented by mr W last updated on 14/Feb/23

yes, there are many right methods and there are also many wrong methods.

$${yes},\:{there}\:{are}\:{many}\:{right}\:{methods}\:{and} \\ $$$${there}\:{are}\:{also}\:{many}\:{wrong}\:{methods}. \\ $$

Commented by mr W last updated on 14/Feb/23

now your answer is correct. when you think your solution is simple, it′s your right to think what you think.

$${now}\:{your}\:{answer}\:{is}\:{correct}.\:{when}\:{you} \\ $$$${think}\:{your}\:{solution}\:{is}\:{simple},\:{it}'{s} \\ $$$${your}\:{right}\:{to}\:{think}\:{what}\:{you}\:{think}. \\ $$

Commented by a.lgnaoui last updated on 14/Feb/23

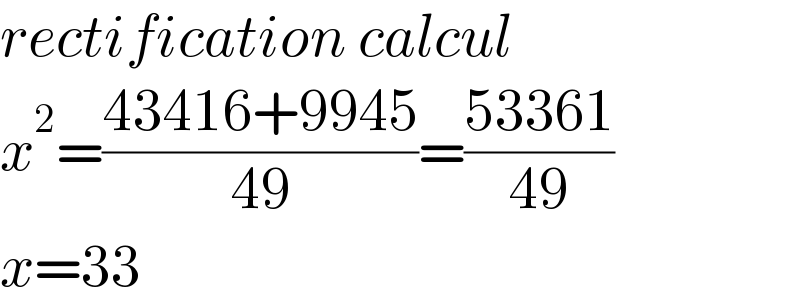
rectification calcul x^2 =((43416+9945)/(49))=((53361)/(49)) x=33

$${rectification}\:{calcul} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{43416}+\mathrm{9945}}{\mathrm{49}}=\frac{\mathrm{53361}}{\mathrm{49}} \\ $$$${x}=\mathrm{33} \\ $$

Commented by a.lgnaoui last updated on 14/Feb/23

its only probleme operation calcul

$${its}\:{only}\:\:{probleme}\:{operation} \\ $$$${calcul} \\ $$

Commented by a.lgnaoui last updated on 14/Feb/23

its a simple probleme calcul sorry.

$${its}\:{a}\:{simple}\:{probleme}\:{calcul} \\ $$$${sorry}. \\ $$

Commented by ajfour last updated on 14/Feb/23

dont u see the font size u use, how do you type so big? guess i knew..!

$${dont}\:{u}\:{see}\:{the}\:{font}\:{size}\:{u}\:{use}, \\ $$$${how}\:{do}\:{you}\:{type}\:{so}\:{big}? \\ $$$${guess}\:{i}\:{knew}..! \\ $$

Commented by a.lgnaoui last updated on 14/Feb/23

yes ok

$${yes}\:{ok} \\ $$

Commented by Rupesh123 last updated on 15/Feb/23

Good job!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com