Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

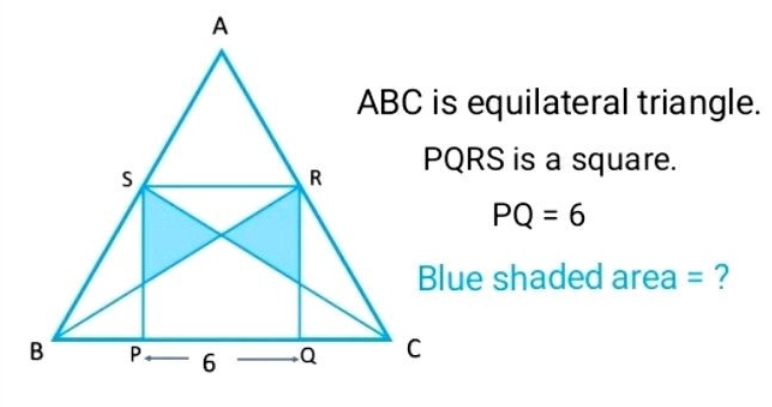
Question Number 187146 by Rupesh123 last updated on 14/Feb/23

Answered by a.lgnaoui last updated on 14/Feb/23

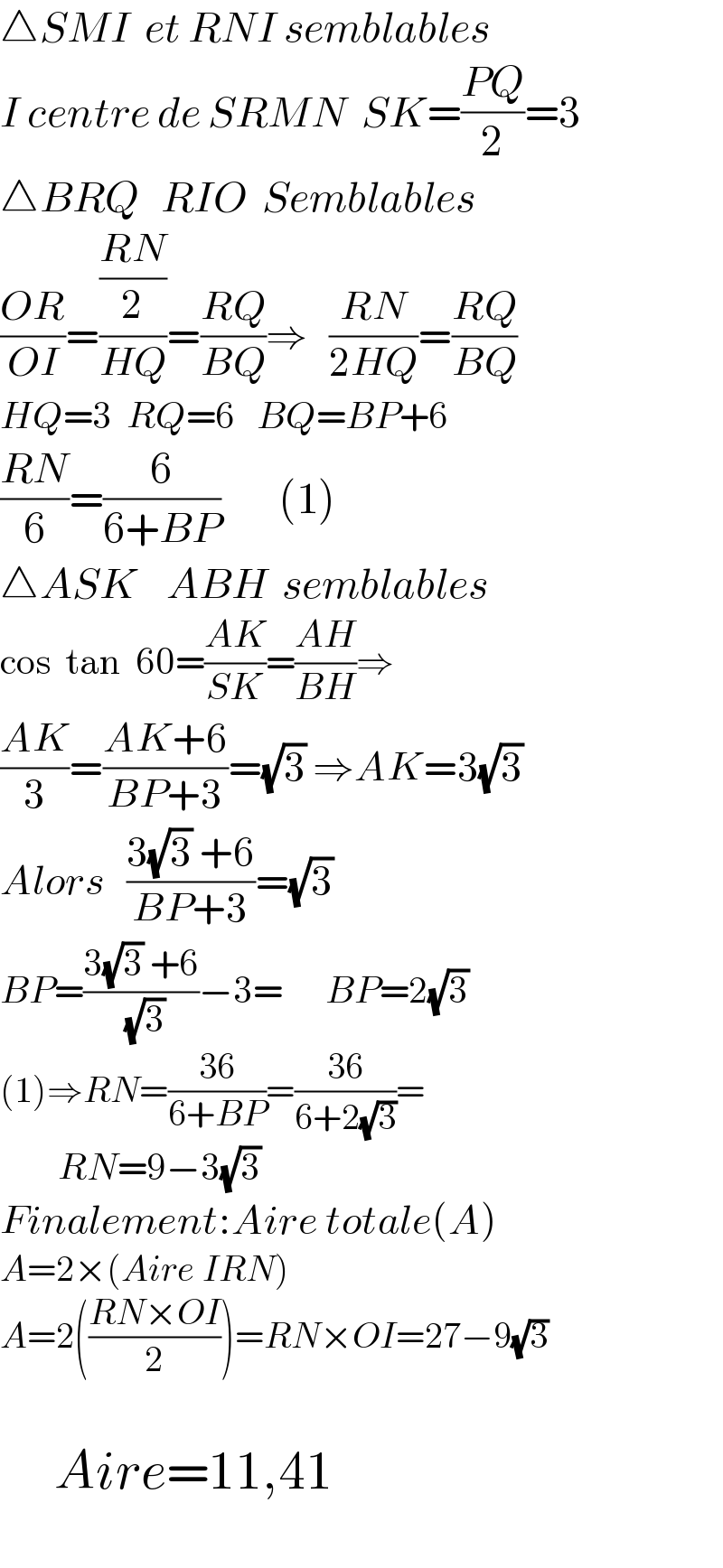
△SMI et RNI semblables I centre de SRMN SK=((PQ)/2)=3 △BRQ RIO Semblables ((OR)/(OI))=(((RN)/2)/(HQ))=((RQ)/(BQ))⇒ ((RN)/(2HQ))=((RQ)/(BQ)) HQ=3 RQ=6 BQ=BP+6 ((RN)/6)=(6/(6+BP)) (1) △ASK ABH semblables cos tan 60=((AK)/(SK))=((AH)/(BH))⇒ ((AK)/3)=((AK+6)/(BP+3))=(√3) ⇒AK=3(√3) Alors ((3(√3) +6)/(BP+3))=(√3) BP=((3(√3) +6)/( (√3)))−3= BP=2(√3) (1)⇒RN=((36)/(6+BP))=((36)/(6+2(√3)))= RN=9−3(√3) Finalement:Aire totale(A) A=2×(Aire IRN) A=2(((RN×OI)/2))=RN×OI=27−9(√3) Aire=11,41

$$\bigtriangleup{SMI}\:\:{et}\:{RNI}\:{semblables}\:\:\: \\ $$$${I}\:{centre}\:{de}\:{SRMN}\:\:{SK}=\frac{{PQ}}{\mathrm{2}}=\mathrm{3} \\ $$$$\bigtriangleup{BRQ}\:\:\:{RIO}\:\:{Semblables} \\ $$$$\frac{{OR}}{{OI}}=\frac{\frac{{RN}}{\mathrm{2}}}{{HQ}}=\frac{{RQ}}{{BQ}}\Rightarrow\:\:\:\frac{{RN}}{\mathrm{2}{HQ}}=\frac{{RQ}}{{BQ}} \\ $$$${HQ}=\mathrm{3}\:\:{RQ}=\mathrm{6}\:\:\:{BQ}={BP}+\mathrm{6} \\ $$$$\frac{{RN}}{\mathrm{6}}=\frac{\mathrm{6}}{\mathrm{6}+{BP}}\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup{ASK}\:\:\:\:{ABH}\:\:{semblables} \\ $$$$\mathrm{cos}\:\:\mathrm{tan}\:\:\mathrm{60}=\frac{{AK}}{{SK}}=\frac{{AH}}{{BH}}\Rightarrow \\ $$$$\frac{{AK}}{\mathrm{3}}=\frac{{AK}+\mathrm{6}}{{BP}+\mathrm{3}}=\sqrt{\mathrm{3}}\:\Rightarrow{AK}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${Alors}\:\:\:\frac{\mathrm{3}\sqrt{\mathrm{3}}\:+\mathrm{6}}{{BP}+\mathrm{3}}=\sqrt{\mathrm{3}} \\ $$$${BP}=\frac{\mathrm{3}\sqrt{\mathrm{3}}\:+\mathrm{6}}{\:\sqrt{\mathrm{3}}}−\mathrm{3}=\:\:\:\:\:\:{BP}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{1}\right)\Rightarrow{RN}=\frac{\mathrm{36}}{\mathrm{6}+{BP}}=\frac{\mathrm{36}}{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{3}}}= \\ $$$$\:\:\:\:\:\:\:\:{RN}=\mathrm{9}−\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${Finalement}:{Aire}\:{totale}\left({A}\right) \\ $$$${A}=\mathrm{2}×\left({Aire}\:{IRN}\right) \\ $$$${A}=\mathrm{2}\left(\frac{{RN}×{OI}}{\mathrm{2}}\right)={RN}×{OI}=\mathrm{27}−\mathrm{9}\sqrt{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:{Aire}=\mathrm{11},\mathrm{41} \\ $$$$ \\ $$

Commented by Rupesh123 last updated on 14/Feb/23

Excellent

Answered by mr W last updated on 14/Feb/23

say side length of equilateral is s. (((((√3)s)/2)−6)/(((√3)s)/2))=(6/s) ⇒s=6+4(√3) BP=(6/( (√3)))=2(√3) BQ=6+4(√3)−2(√3)=6+2(√3) ((TP)/(RQ))=((BP)/(BQ)) ⇒TP=((2(√3)×6)/(6+2(√3)))=3(√3)−3 ⇒ST=6−(3(√3)−3)=3(3−(√3)) A_(blue) =(6/2)×ST=9(3−(√3))≈11.412

$${say}\:{side}\:{length}\:{of}\:{equilateral}\:{is}\:{s}. \\ $$$$\frac{\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}−\mathrm{6}}{\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}}=\frac{\mathrm{6}}{{s}} \\ $$$$\Rightarrow{s}=\mathrm{6}+\mathrm{4}\sqrt{\mathrm{3}} \\ $$$${BP}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{3}}}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${BQ}=\mathrm{6}+\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{3}}=\mathrm{6}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\frac{{TP}}{{RQ}}=\frac{{BP}}{{BQ}} \\ $$$$\Rightarrow{TP}=\frac{\mathrm{2}\sqrt{\mathrm{3}}×\mathrm{6}}{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{3}}}=\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{3} \\ $$$$\Rightarrow{ST}=\mathrm{6}−\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{3}\right)=\mathrm{3}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right) \\ $$$${A}_{{blue}} =\frac{\mathrm{6}}{\mathrm{2}}×{ST}=\mathrm{9}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\approx\mathrm{11}.\mathrm{412} \\ $$

Commented by Rupesh123 last updated on 14/Feb/23

Excellent

Terms of Service

Privacy Policy

Contact: info@tinkutara.com