Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 187029 by yaslm last updated on 12/Feb/23

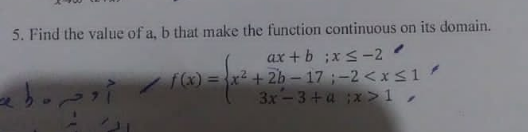
Answered by cortano12 last updated on 12/Feb/23

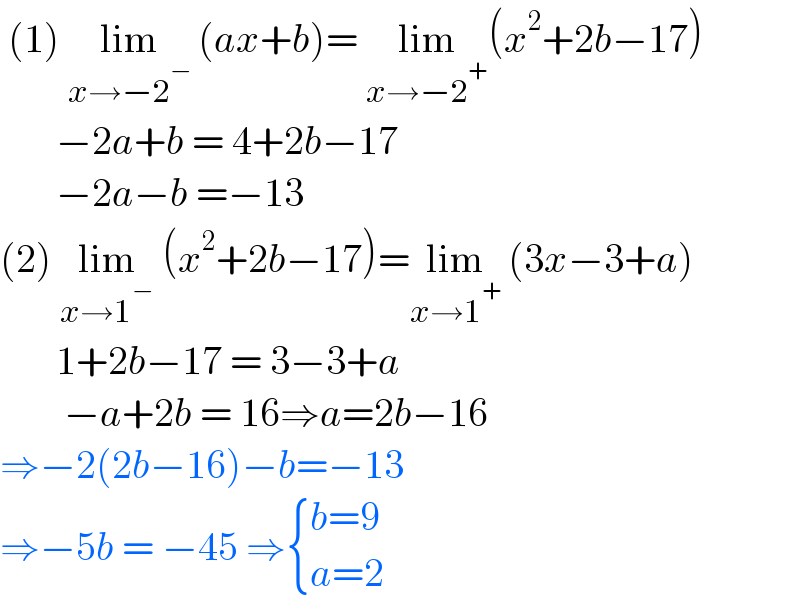
(1) lim_(x→−2^− ) (ax+b)= lim_(x→−2^+ ) (x^2 +2b−17) −2a+b = 4+2b−17 −2a−b =−13 (2) lim_(x→1^− ) (x^2 +2b−17)=lim_(x→1^+ ) (3x−3+a) 1+2b−17 = 3−3+a −a+2b = 16⇒a=2b−16 ⇒−2(2b−16)−b=−13 ⇒−5b = −45 ⇒ { ((b=9)),((a=2)) :}

$$\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow−\mathrm{2}^{−} } {\mathrm{lim}}\:\left({ax}+{b}\right)=\:\underset{{x}\rightarrow−\mathrm{2}^{+} } {\mathrm{lim}}\left({x}^{\mathrm{2}} +\mathrm{2}{b}−\mathrm{17}\right) \\ $$$$\:\:\:\:\:\:\:−\mathrm{2}{a}+{b}\:=\:\mathrm{4}+\mathrm{2}{b}−\mathrm{17} \\ $$$$\:\:\:\:\:\:\:−\mathrm{2}{a}−{b}\:=−\mathrm{13} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\left({x}^{\mathrm{2}} +\mathrm{2}{b}−\mathrm{17}\right)=\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\left(\mathrm{3}{x}−\mathrm{3}+{a}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{1}+\mathrm{2}{b}−\mathrm{17}\:=\:\mathrm{3}−\mathrm{3}+{a} \\ $$$$\:\:\:\:\:\:\:\:−{a}+\mathrm{2}{b}\:=\:\mathrm{16}\Rightarrow{a}=\mathrm{2}{b}−\mathrm{16} \\ $$$$\Rightarrow−\mathrm{2}\left(\mathrm{2}{b}−\mathrm{16}\right)−{b}=−\mathrm{13} \\ $$$$\Rightarrow−\mathrm{5}{b}\:=\:−\mathrm{45}\:\Rightarrow\begin{cases}{{b}=\mathrm{9}}\\{{a}=\mathrm{2}}\end{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com