Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 186996 by Mingma last updated on 12/Feb/23

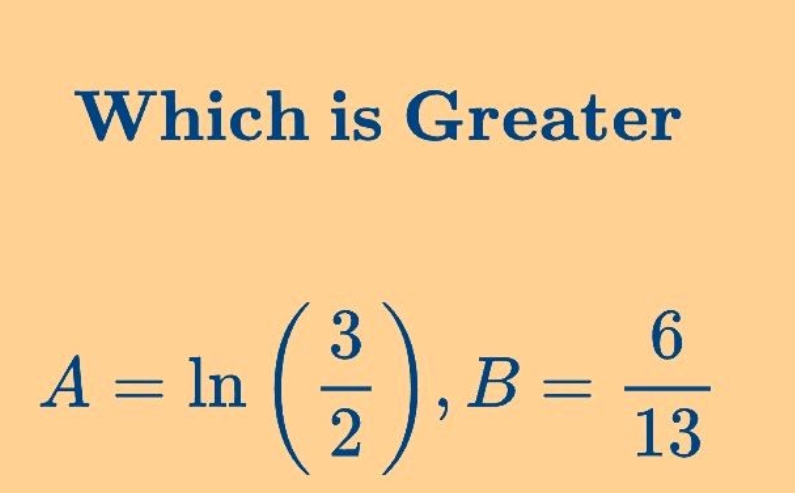
Answered by aba last updated on 12/Feb/23

0<ln(3/2)<6/13

$$\mathrm{0}<\mathrm{ln}\left(\mathrm{3}/\mathrm{2}\right)<\mathrm{6}/\mathrm{13} \\ $$

Commented by MJS_new last updated on 12/Feb/23

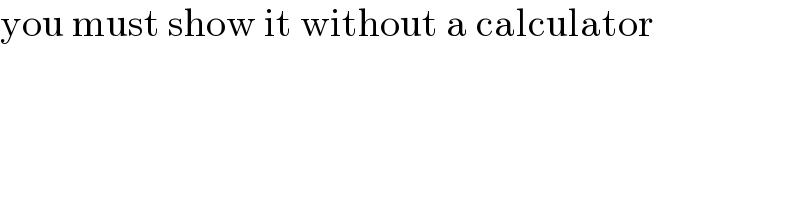
you must show it without a calculator

$$\mathrm{you}\:\mathrm{must}\:\mathrm{show}\:\mathrm{it}\:\mathrm{without}\:\mathrm{a}\:\mathrm{calculator} \\ $$

Commented by aba last updated on 12/Feb/23

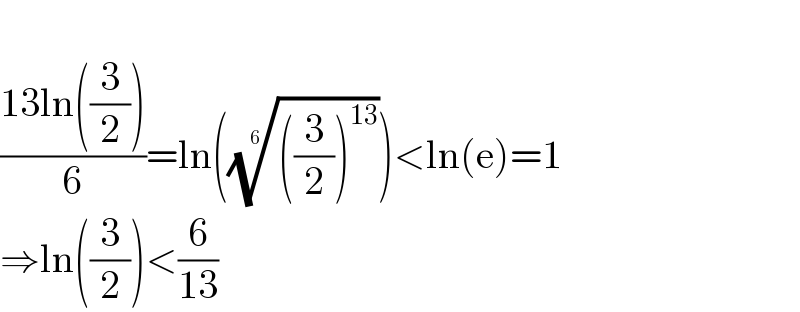
((13ln((3/2)))/6)=ln(((((3/2))^(13) ))^(1/6) )<ln(e)=1 ⇒ln((3/2))<(6/(13))

$$ \\ $$$$\frac{\mathrm{13ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{6}}=\mathrm{ln}\left(\sqrt[{\mathrm{6}}]{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{13}} }\right)<\mathrm{ln}\left(\mathrm{e}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)<\frac{\mathrm{6}}{\mathrm{13}} \\ $$

Commented by Frix last updated on 12/Feb/23

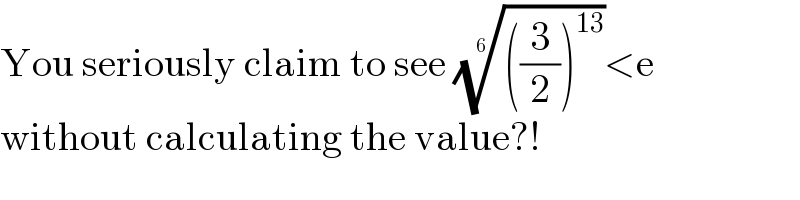
You seriously claim to see ((((3/2))^(13) ))^(1/6) <e without calculating the value?!

$$\mathrm{You}\:\mathrm{seriously}\:\mathrm{claim}\:\mathrm{to}\:\mathrm{see}\:\sqrt[{\mathrm{6}}]{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{13}} }<\mathrm{e} \\ $$$$\mathrm{without}\:\mathrm{calculating}\:\mathrm{the}\:\mathrm{value}?! \\ $$

Commented by aba last updated on 12/Feb/23

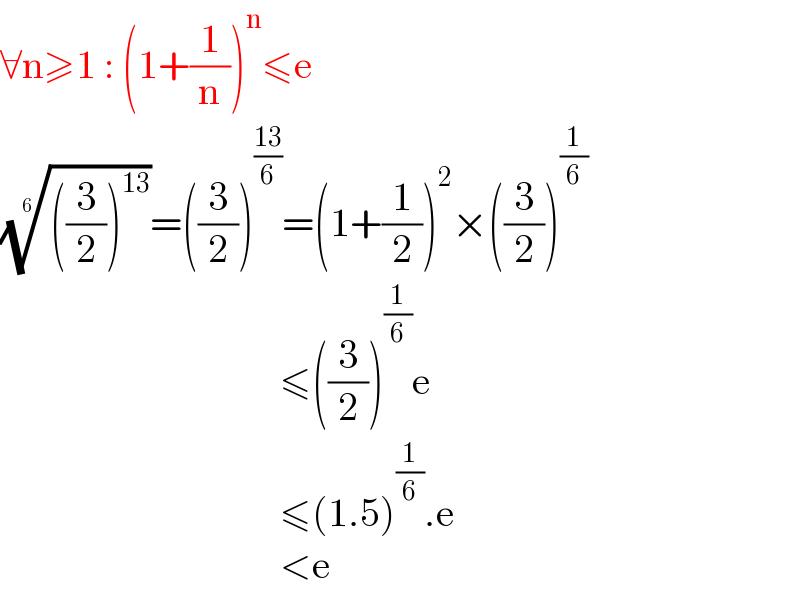
∀n≥1 : (1+(1/n))^n ≤e ((((3/2))^(13) ))^(1/6) =((3/2))^((13)/6) =(1+(1/2))^2 ×((3/2))^(1/6) ≤((3/2))^(1/6) e ≤(1.5)^(1/6) .e <e

$$\forall\mathrm{n}\geqslant\mathrm{1}\::\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{n}} \leqslant\mathrm{e} \\ $$$$\sqrt[{\mathrm{6}}]{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{13}} }=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{13}}{\mathrm{6}}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} \mathrm{e} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant\left(\mathrm{1}.\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} .\mathrm{e} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:<\mathrm{e} \\ $$

Commented by Mingma last updated on 12/Feb/23

Good!

Commented by mr W last updated on 12/Feb/23

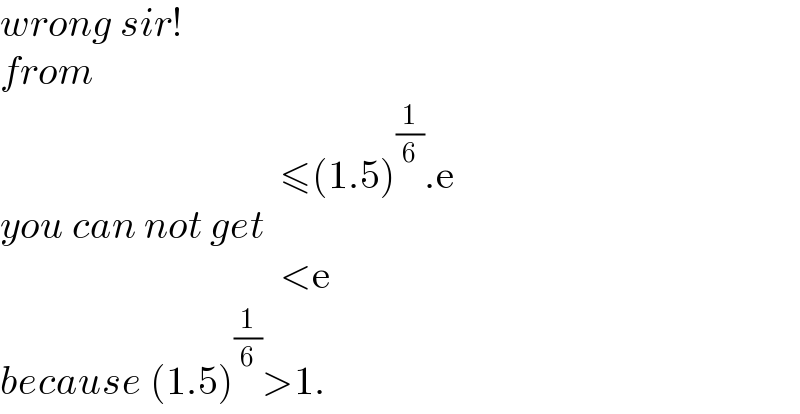
wrong sir! from ≤(1.5)^(1/6) .e you can not get <e because (1.5)^(1/6) >1.

$${wrong}\:{sir}! \\ $$$${from} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant\left(\mathrm{1}.\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} .\mathrm{e} \\ $$$${you}\:{can}\:{not}\:{get} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:<\mathrm{e} \\ $$$${because}\:\left(\mathrm{1}.\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} >\mathrm{1}. \\ $$

Commented by aba last updated on 12/Feb/23

����

Commented by Frix last updated on 12/Feb/23

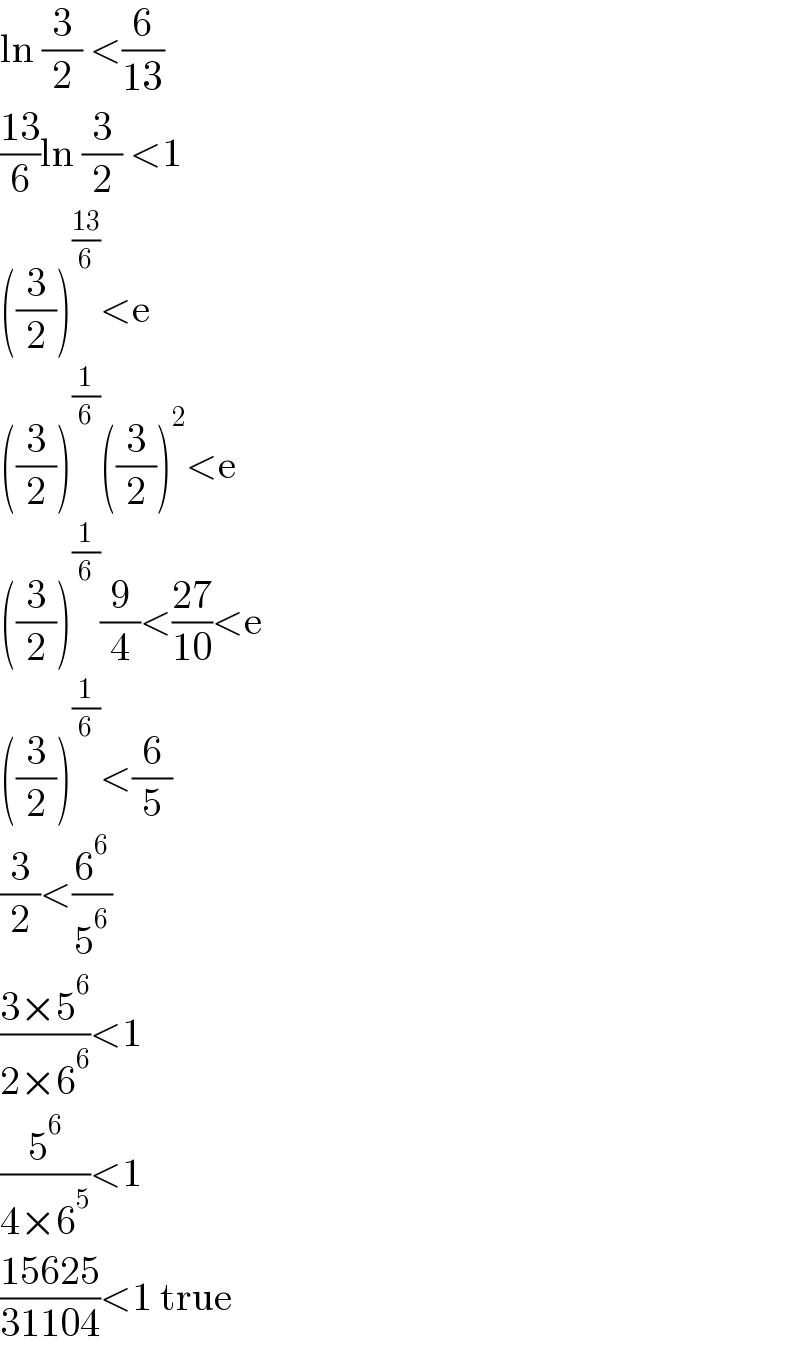
ln (3/2) <(6/(13)) ((13)/6)ln (3/2) <1 ((3/2))^((13)/6) <e ((3/2))^(1/6) ((3/2))^2 <e ((3/2))^(1/6) (9/4)<((27)/(10))<e ((3/2))^(1/6) <(6/5) (3/2)<(6^6 /5^6 ) ((3×5^6 )/(2×6^6 ))<1 (5^6 /(4×6^5 ))<1 ((15625)/(31104))<1 true

$$\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{2}}\:<\frac{\mathrm{6}}{\mathrm{13}} \\ $$$$\frac{\mathrm{13}}{\mathrm{6}}\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{2}}\:<\mathrm{1} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{13}}{\mathrm{6}}} <\mathrm{e} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} <\mathrm{e} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} \frac{\mathrm{9}}{\mathrm{4}}<\frac{\mathrm{27}}{\mathrm{10}}<\mathrm{e} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} <\frac{\mathrm{6}}{\mathrm{5}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}<\frac{\mathrm{6}^{\mathrm{6}} }{\mathrm{5}^{\mathrm{6}} } \\ $$$$\frac{\mathrm{3}×\mathrm{5}^{\mathrm{6}} }{\mathrm{2}×\mathrm{6}^{\mathrm{6}} }<\mathrm{1} \\ $$$$\frac{\mathrm{5}^{\mathrm{6}} }{\mathrm{4}×\mathrm{6}^{\mathrm{5}} }<\mathrm{1} \\ $$$$\frac{\mathrm{15625}}{\mathrm{31104}}<\mathrm{1}\:\mathrm{true} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com