Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 186983 by cortano12 last updated on 12/Feb/23

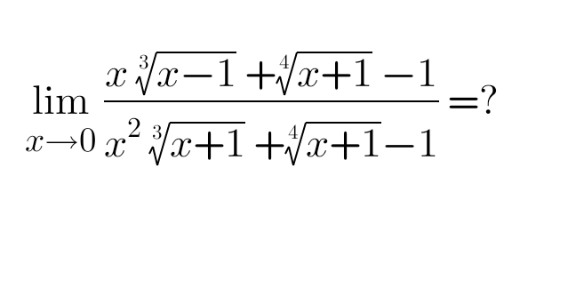
Answered by CElcedricjunior last updated on 12/Feb/23

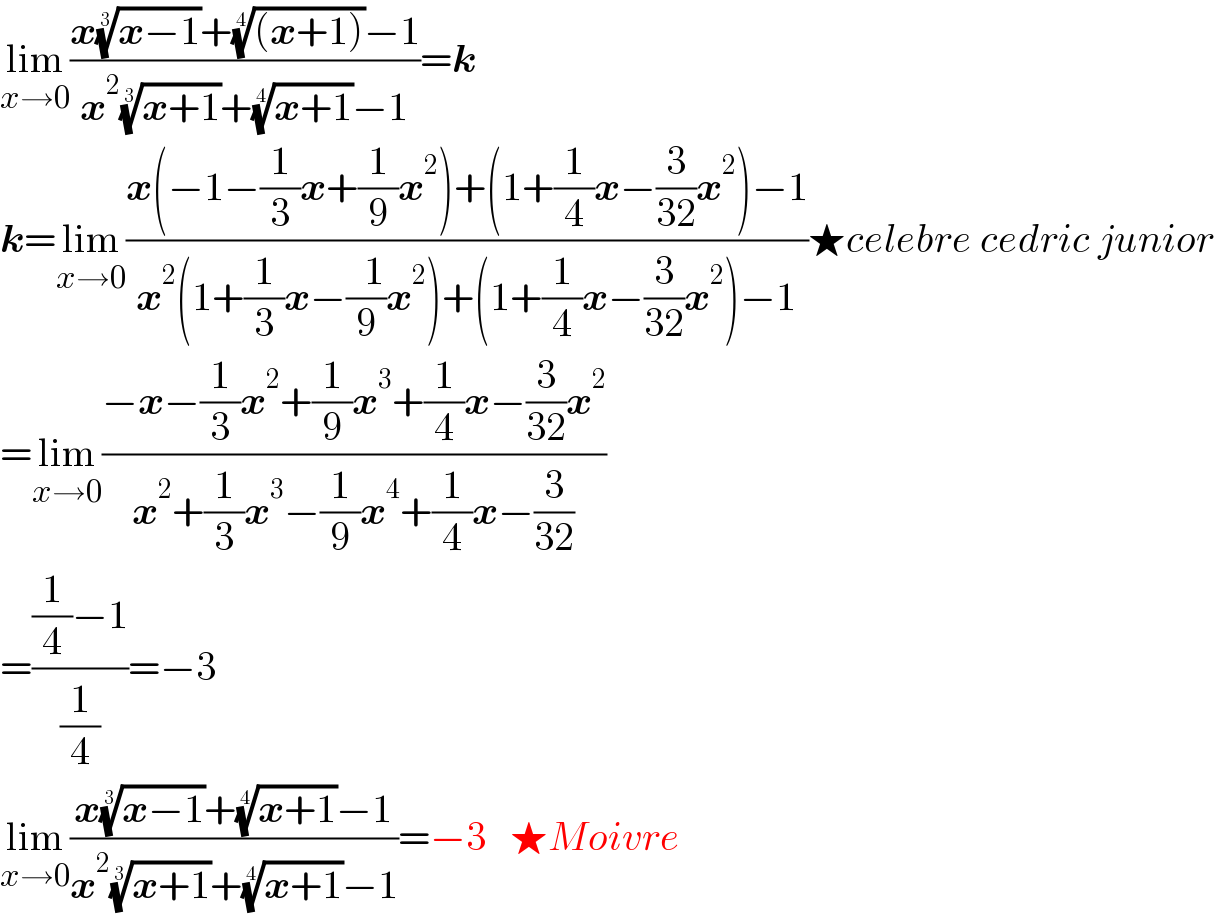
lim_(x→0) ((x((x−1))^(1/3) +(((x+1)))^(1/4) −1)/(x^2 ((x+1))^(1/3) +((x+1))^(1/4) −1))=k k=lim_(x→0) ((x(−1−(1/3)x+(1/9)x^2 )+(1+(1/4)x−(3/(32))x^2 )−1)/(x^2 (1+(1/3)x−(( 1)/9)x^2 )+(1+(1/4)x−(3/(32))x^2 )−1))★celebre cedric junior =lim_(x→0) ((−x−(1/3)x^2 +(1/9)x^3 +(1/4)x−(3/(32))x^2 )/(x^2 +(1/3)x^3 −(1/9)x^4 +(1/4)x−(3/(32)))) =(((1/4)−1)/(1/4))=−3 lim_(x→0) ((x((x−1))^(1/3) +((x+1))^(1/4) −1)/(x^2 ((x+1))^(1/3) +((x+1))^(1/4) −1))=−3 ★Moivre

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{x}}\sqrt[{\mathrm{3}}]{\boldsymbol{{x}}−\mathrm{1}}+\sqrt[{\mathrm{4}}]{\left(\boldsymbol{{x}}+\mathrm{1}\right)}−\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\boldsymbol{{x}}+\mathrm{1}}+\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}+\mathrm{1}}−\mathrm{1}}=\boldsymbol{{k}} \\ $$$$\boldsymbol{{k}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{x}}\left(−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{x}}+\frac{\mathrm{1}}{\mathrm{9}}\boldsymbol{{x}}^{\mathrm{2}} \right)+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{x}}−\frac{\mathrm{3}}{\mathrm{32}}\boldsymbol{{x}}^{\mathrm{2}} \right)−\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{x}}−\frac{\:\:\mathrm{1}}{\mathrm{9}}\boldsymbol{{x}}^{\mathrm{2}} \right)+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{x}}−\frac{\mathrm{3}}{\mathrm{32}}\boldsymbol{{x}}^{\mathrm{2}} \right)−\mathrm{1}}\bigstar{celebre}\:{cedric}\:{junior} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\boldsymbol{{x}}−\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}\boldsymbol{{x}}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{x}}−\frac{\mathrm{3}}{\mathrm{32}}\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{x}}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{9}}\boldsymbol{{x}}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{x}}−\frac{\mathrm{3}}{\mathrm{32}}} \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}}=−\mathrm{3} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{x}}\sqrt[{\mathrm{3}}]{\boldsymbol{{x}}−\mathrm{1}}+\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}+\mathrm{1}}−\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\boldsymbol{{x}}+\mathrm{1}}+\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}+\mathrm{1}}−\mathrm{1}}=−\mathrm{3}\:\:\:\bigstar{Moivre} \\ $$

Answered by ARUNG_Brandon_MBU last updated on 12/Feb/23

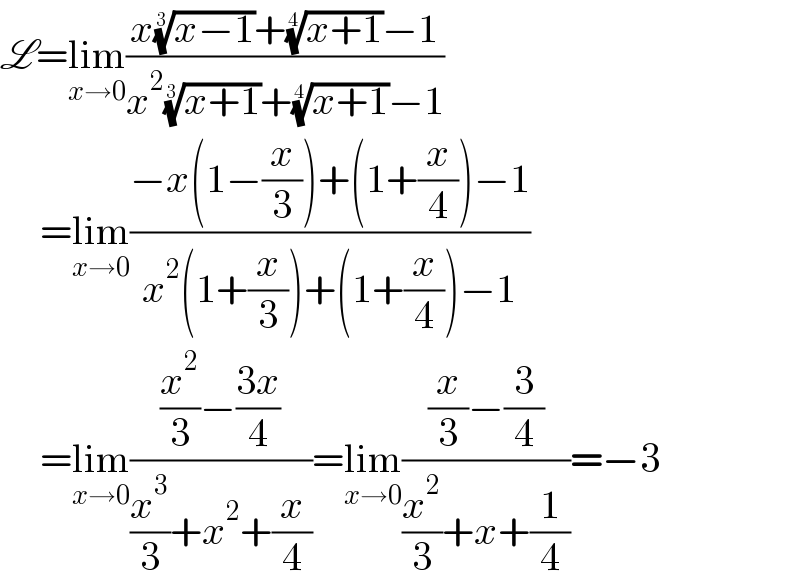
L=lim_(x→0) ((x((x−1))^(1/3) +((x+1))^(1/4) −1)/(x^2 ((x+1))^(1/3) +((x+1))^(1/4) −1)) =lim_(x→0) ((−x(1−(x/3))+(1+(x/4))−1)/(x^2 (1+(x/3))+(1+(x/4))−1)) =lim_(x→0) (((x^2 /3)−((3x)/4))/((x^3 /3)+x^2 +(x/4)))=lim_(x→0) (((x/3)−(3/4))/((x^2 /3)+x+(1/4)))=−3

$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\sqrt[{\mathrm{3}}]{{x}−\mathrm{1}}+\sqrt[{\mathrm{4}}]{{x}+\mathrm{1}}−\mathrm{1}}{{x}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}+\sqrt[{\mathrm{4}}]{{x}+\mathrm{1}}−\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−{x}\left(\mathrm{1}−\frac{{x}}{\mathrm{3}}\right)+\left(\mathrm{1}+\frac{{x}}{\mathrm{4}}\right)−\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}}{\mathrm{3}}\right)+\left(\mathrm{1}+\frac{{x}}{\mathrm{4}}\right)−\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{3}{x}}{\mathrm{4}}}{\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{x}^{\mathrm{2}} +\frac{{x}}{\mathrm{4}}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}}{\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{4}}}{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+{x}+\frac{\mathrm{1}}{\mathrm{4}}}=−\mathrm{3} \\ $$

Answered by cortano12 last updated on 14/Feb/23

Terms of Service

Privacy Policy

Contact: info@tinkutara.com