
Question Number 186821 by yaslm last updated on 10/Feb/23
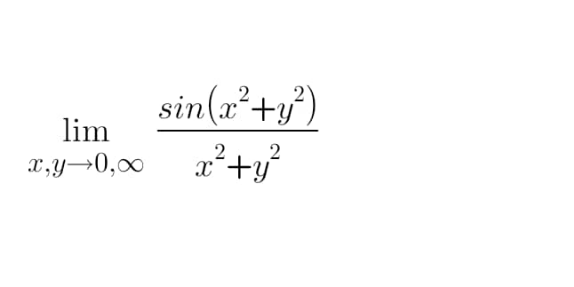
Answered by CElcedricjunior last updated on 11/Feb/23
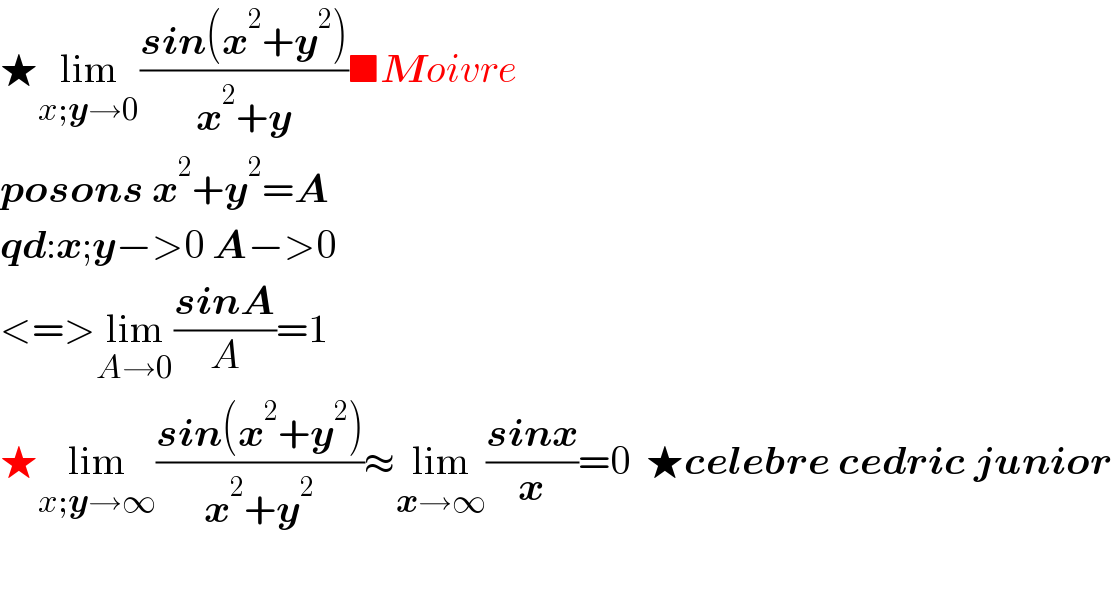
$$\bigstar\underset{{x};\boldsymbol{{y}}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)}{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}}\blacksquare\boldsymbol{{M}}{oivre} \\ $$$$\boldsymbol{{posons}}\:\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} =\boldsymbol{{A}} \\ $$$$\boldsymbol{{qd}}:\boldsymbol{{x}};\boldsymbol{{y}}−>\mathrm{0}\:\boldsymbol{{A}}−>\mathrm{0} \\ $$$$<=>\underset{{A}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{sinA}}}{{A}}=\mathrm{1} \\ $$$$\bigstar\underset{{x};\boldsymbol{{y}}\rightarrow\infty} {\mathrm{lim}}\frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)}{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} }\approx\underset{\boldsymbol{{x}}\rightarrow\infty} {\mathrm{lim}}\frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}=\mathrm{0}\:\:\bigstar\boldsymbol{{celebre}}\:\boldsymbol{{cedric}}\:\boldsymbol{{junior}} \\ $$$$ \\ $$
