
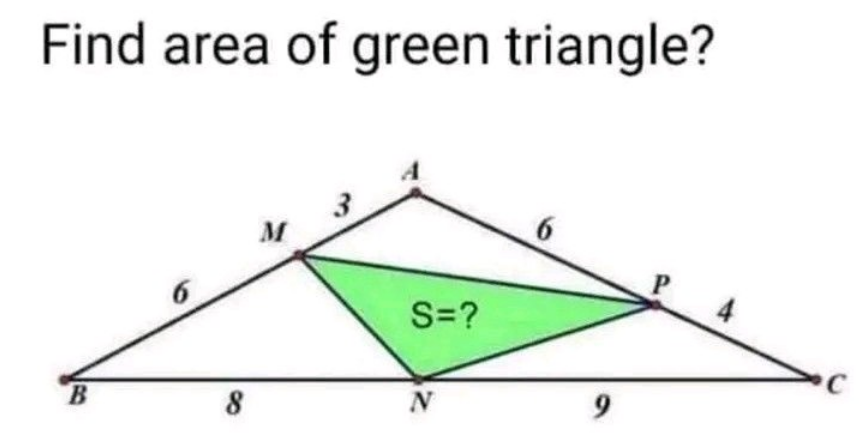
Question Number 186782 by Rupesh123 last updated on 10/Feb/23
Answered by HeferH last updated on 10/Feb/23
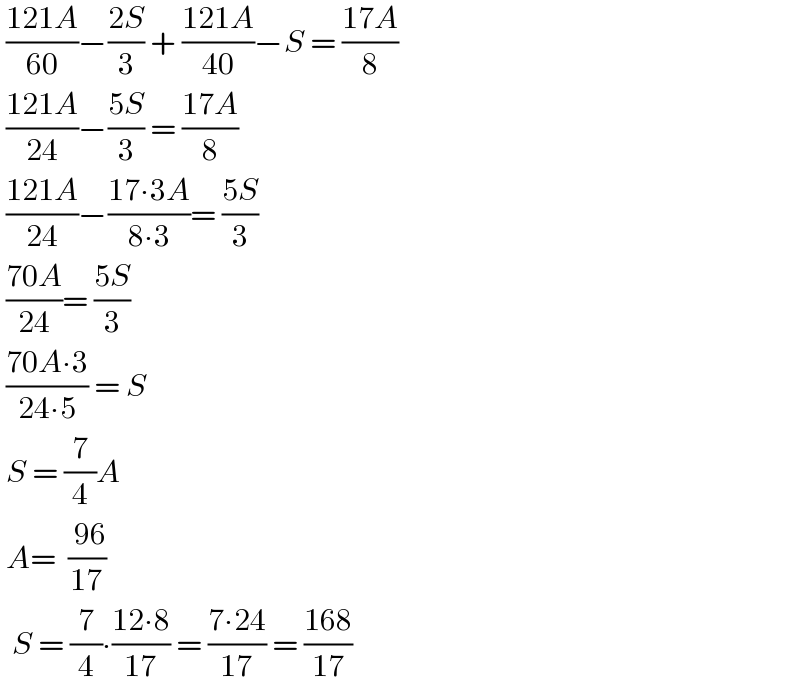
$$\:\frac{\mathrm{121}{A}}{\mathrm{60}}−\frac{\mathrm{2}{S}}{\mathrm{3}}\:+\:\frac{\mathrm{121}{A}}{\mathrm{40}}−{S}\:=\:\frac{\mathrm{17}{A}}{\mathrm{8}} \\ $$$$\:\frac{\mathrm{121}{A}}{\mathrm{24}}−\frac{\mathrm{5}{S}}{\mathrm{3}}\:=\:\frac{\mathrm{17}{A}}{\mathrm{8}} \\ $$$$\:\frac{\mathrm{121}{A}}{\mathrm{24}}−\frac{\mathrm{17}\centerdot\mathrm{3}{A}}{\mathrm{8}\centerdot\mathrm{3}}=\:\frac{\mathrm{5}{S}}{\mathrm{3}} \\ $$$$\:\frac{\mathrm{70}{A}}{\mathrm{24}}=\:\frac{\mathrm{5}{S}}{\mathrm{3}} \\ $$$$\:\frac{\mathrm{70}{A}\centerdot\mathrm{3}}{\mathrm{24}\centerdot\mathrm{5}}\:=\:{S} \\ $$$$\:{S}\:=\:\frac{\mathrm{7}}{\mathrm{4}}{A} \\ $$$$\:{A}=\:\:\frac{\:\mathrm{96}}{\mathrm{17}} \\ $$$$\:\:{S}\:=\:\frac{\mathrm{7}}{\mathrm{4}}\centerdot\frac{\mathrm{12}\centerdot\mathrm{8}}{\mathrm{17}}\:=\:\frac{\mathrm{7}\centerdot\mathrm{24}}{\mathrm{17}}\:=\:\frac{\mathrm{168}}{\mathrm{17}} \\ $$
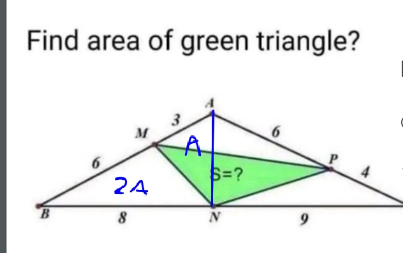
Commented by HeferH last updated on 10/Feb/23
Answered by nikif99 last updated on 10/Feb/23
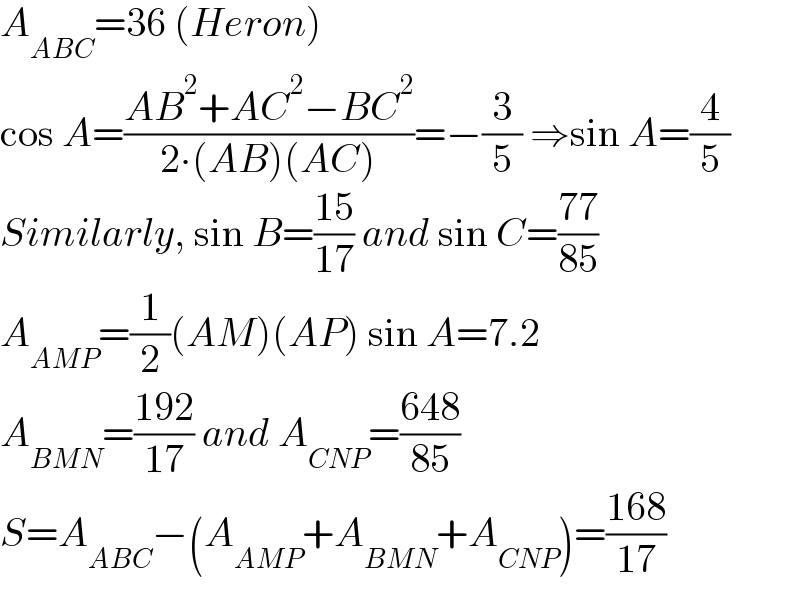
$${A}_{{ABC}} =\mathrm{36}\:\left({Heron}\right) \\ $$$$\mathrm{cos}\:{A}=\frac{{AB}^{\mathrm{2}} +{AC}^{\mathrm{2}} −{BC}^{\mathrm{2}} }{\mathrm{2}\centerdot\left({AB}\right)\left({AC}\right)}=−\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\mathrm{sin}\:{A}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${Similarly},\:\mathrm{sin}\:{B}=\frac{\mathrm{15}}{\mathrm{17}}\:{and}\:\mathrm{sin}\:{C}=\frac{\mathrm{77}}{\mathrm{85}} \\ $$$${A}_{{AMP}} =\frac{\mathrm{1}}{\mathrm{2}}\left({AM}\right)\left({AP}\right)\:\mathrm{sin}\:{A}=\mathrm{7}.\mathrm{2} \\ $$$${A}_{{BMN}} =\frac{\mathrm{192}}{\mathrm{17}}\:{and}\:{A}_{{CNP}} =\frac{\mathrm{648}}{\mathrm{85}} \\ $$$${S}={A}_{{ABC}} −\left({A}_{{AMP}} +{A}_{{BMN}} +{A}_{{CNP}} \right)=\frac{\mathrm{168}}{\mathrm{17}} \\ $$
Answered by mr W last updated on 10/Feb/23
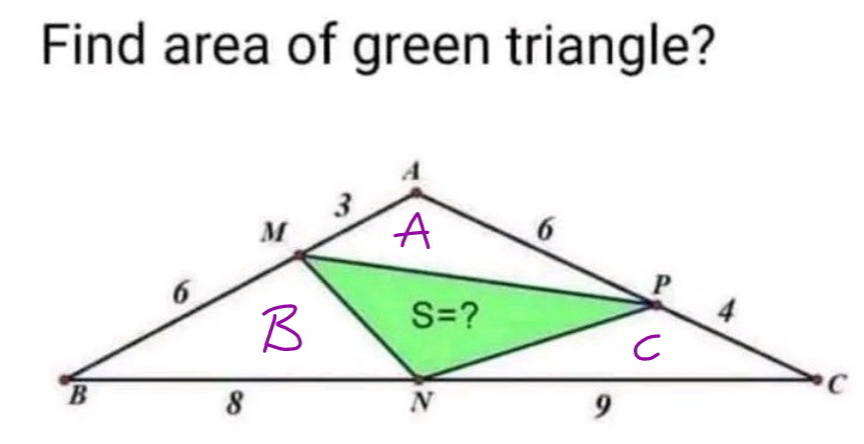
Commented by mr W last updated on 10/Feb/23

$$\Delta={area}\:{of}\:\Delta{ABC} \\ $$$$\Delta=\frac{\sqrt{\left(\mathrm{9}+\mathrm{17}+\mathrm{10}\right)\left(−\mathrm{9}+\mathrm{17}+\mathrm{10}\right)\left(\mathrm{9}−\mathrm{17}+\mathrm{10}\right)\left(\mathrm{9}+\mathrm{17}−\mathrm{10}\right)}}{\mathrm{4}} \\ $$$$\:\:\:\:=\mathrm{36} \\ $$$$\frac{{A}}{\Delta}=\frac{\mathrm{3}×\mathrm{6}}{\mathrm{9}×\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\frac{{B}}{\Delta}=\frac{\mathrm{6}×\mathrm{8}}{\mathrm{9}×\mathrm{17}}=\frac{\mathrm{16}}{\mathrm{51}} \\ $$$$\frac{{C}}{\Delta}=\frac{\mathrm{9}×\mathrm{4}}{\mathrm{17}×\mathrm{10}}=\frac{\mathrm{18}}{\mathrm{85}} \\ $$$$\frac{{S}+{A}+{B}+{C}}{\Delta}=\frac{\Delta}{\Delta}=\mathrm{1} \\ $$$$\Rightarrow\frac{{S}}{\Delta}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{16}}{\mathrm{51}}−\frac{\mathrm{18}}{\mathrm{85}}=\frac{\mathrm{14}}{\mathrm{51}} \\ $$$$\Rightarrow{S}=\frac{\mathrm{14}×\mathrm{36}}{\mathrm{51}}=\frac{\mathrm{168}}{\mathrm{17}} \\ $$
