
Question and Answers Forum
Question Number 186637 by Mingma last updated on 07/Feb/23
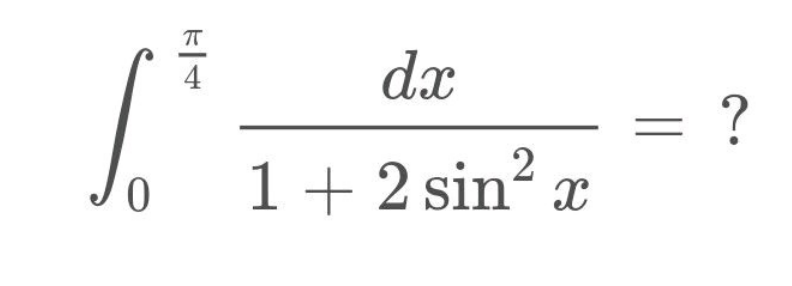
Answered by mr W last updated on 07/Feb/23
![=∫_0 ^(π/4) (dx/(2−(1−2 sin^2 x))) =∫_0 ^(π/4) (dx/(2−cos 2x)) =(1/2)∫_0 ^(π/2) (dx/(2−cos x)) =(1/( (√3)))[tan^(−1) ((√3) tan (x/2))]_0 ^(π/2) =(π/( 3(√3)))](Q186653.png)
Answered by ARUNG_Brandon_MBU last updated on 08/Feb/23
![I=∫_0 ^(π/4) (dx/(1+2sin^2 x))=∫_0 ^(π/4) ((sec^2 x)/(sec^2 x+2tan^2 x))dx =∫_0 ^(π/4) ((sec^2 x)/(3tan^2 x+1))dx=∫_0 ^1 (dt/(3t^2 +1)) =(1/( (√3)))[arctan((√3)t)]_0 ^1 =(π/(3(√3)))](Q186656.png)
| ||
Question and Answers Forum | ||
Question Number 186637 by Mingma last updated on 07/Feb/23 | ||
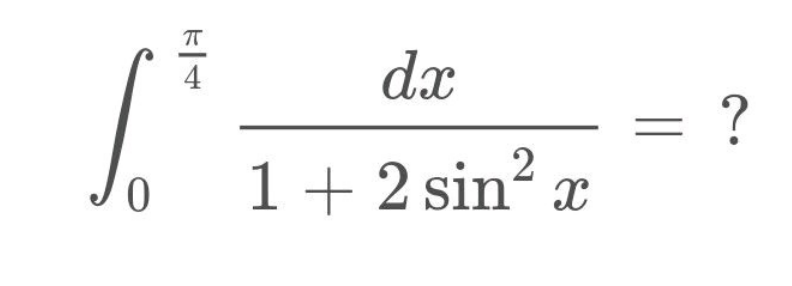 | ||
Answered by mr W last updated on 07/Feb/23 | ||
![=∫_0 ^(π/4) (dx/(2−(1−2 sin^2 x))) =∫_0 ^(π/4) (dx/(2−cos 2x)) =(1/2)∫_0 ^(π/2) (dx/(2−cos x)) =(1/( (√3)))[tan^(−1) ((√3) tan (x/2))]_0 ^(π/2) =(π/( 3(√3)))](Q186653.png) | ||
| ||
Answered by ARUNG_Brandon_MBU last updated on 08/Feb/23 | ||
![I=∫_0 ^(π/4) (dx/(1+2sin^2 x))=∫_0 ^(π/4) ((sec^2 x)/(sec^2 x+2tan^2 x))dx =∫_0 ^(π/4) ((sec^2 x)/(3tan^2 x+1))dx=∫_0 ^1 (dt/(3t^2 +1)) =(1/( (√3)))[arctan((√3)t)]_0 ^1 =(π/(3(√3)))](Q186656.png) | ||
| ||