
Question Number 186026 by Michaelfaraday last updated on 31/Jan/23
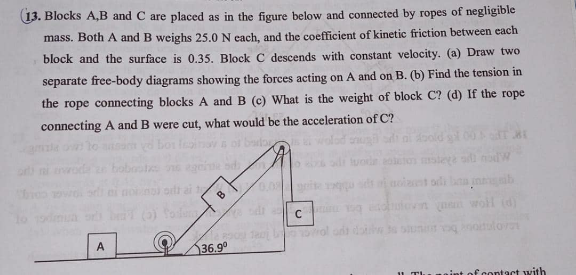
Answered by mr W last updated on 31/Jan/23
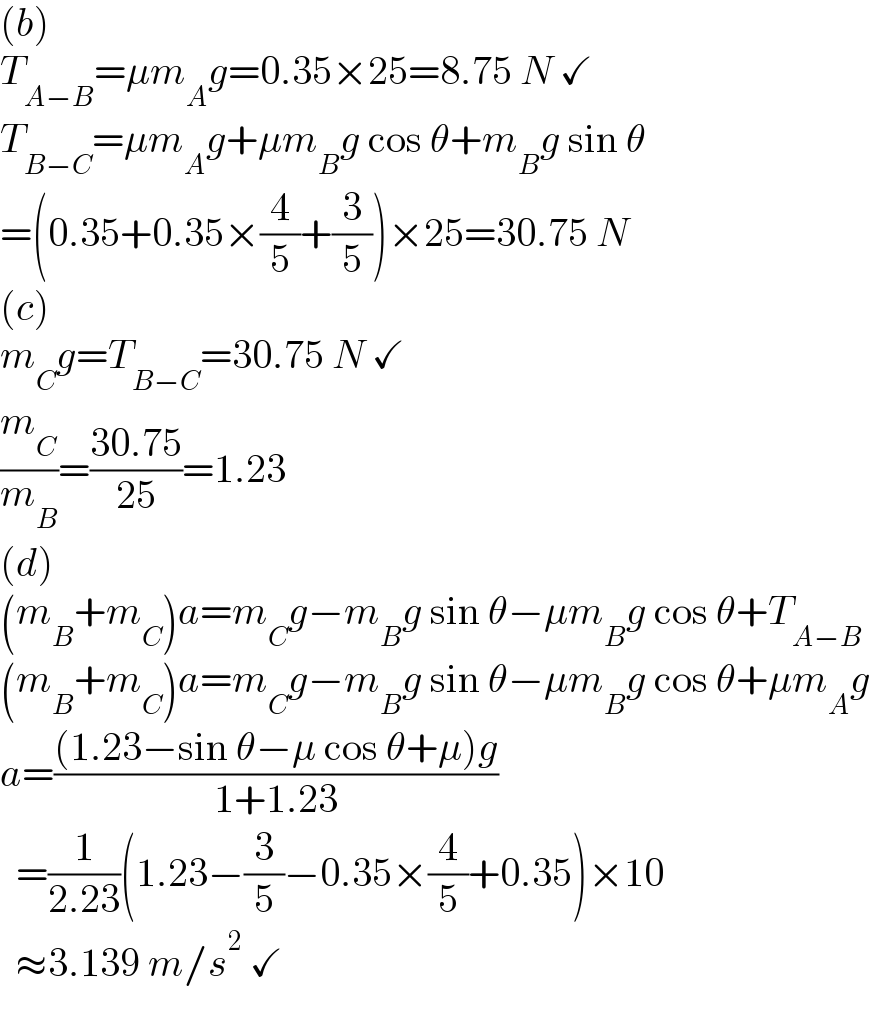
$$\left({b}\right) \\ $$$${T}_{{A}−{B}} =\mu{m}_{{A}} {g}=\mathrm{0}.\mathrm{35}×\mathrm{25}=\mathrm{8}.\mathrm{75}\:{N}\:\checkmark \\ $$$${T}_{{B}−{C}} =\mu{m}_{{A}} {g}+\mu{m}_{{B}} {g}\:\mathrm{cos}\:\theta+{m}_{{B}} {g}\:\mathrm{sin}\:\theta \\ $$$$=\left(\mathrm{0}.\mathrm{35}+\mathrm{0}.\mathrm{35}×\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{5}}\right)×\mathrm{25}=\mathrm{30}.\mathrm{75}\:{N} \\ $$$$\left({c}\right) \\ $$$${m}_{{C}} {g}={T}_{{B}−{C}} =\mathrm{30}.\mathrm{75}\:{N}\:\checkmark \\ $$$$\frac{{m}_{{C}} }{{m}_{{B}} }=\frac{\mathrm{30}.\mathrm{75}}{\mathrm{25}}=\mathrm{1}.\mathrm{23} \\ $$$$\left({d}\right) \\ $$$$\left({m}_{{B}} +{m}_{{C}} \right){a}={m}_{{C}} {g}−{m}_{{B}} {g}\:\mathrm{sin}\:\theta−\mu{m}_{{B}} {g}\:\mathrm{cos}\:\theta+{T}_{{A}−{B}} \\ $$$$\left({m}_{{B}} +{m}_{{C}} \right){a}={m}_{{C}} {g}−{m}_{{B}} {g}\:\mathrm{sin}\:\theta−\mu{m}_{{B}} {g}\:\mathrm{cos}\:\theta+\mu{m}_{{A}} {g} \\ $$$${a}=\frac{\left(\mathrm{1}.\mathrm{23}−\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta+\mu\right){g}}{\mathrm{1}+\mathrm{1}.\mathrm{23}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{23}}\left(\mathrm{1}.\mathrm{23}−\frac{\mathrm{3}}{\mathrm{5}}−\mathrm{0}.\mathrm{35}×\frac{\mathrm{4}}{\mathrm{5}}+\mathrm{0}.\mathrm{35}\right)×\mathrm{10} \\ $$$$\:\:\approx\mathrm{3}.\mathrm{139}\:{m}/{s}^{\mathrm{2}} \:\checkmark \\ $$
