Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 185938 by Mingma last updated on 30/Jan/23

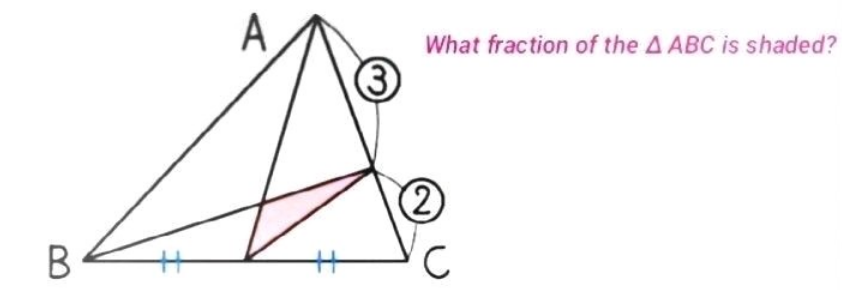
Answered by HeferH last updated on 30/Jan/23

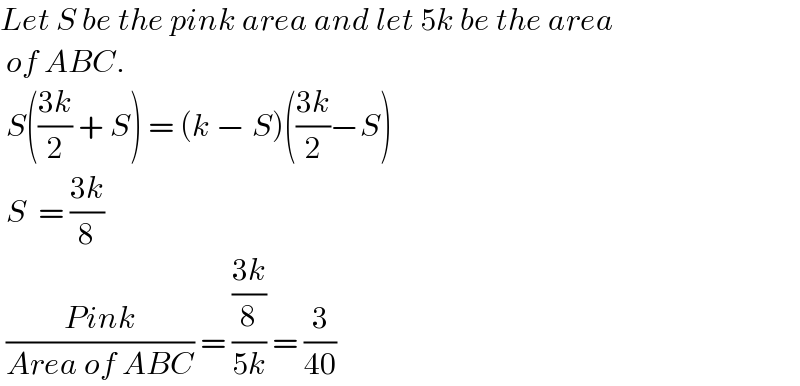
Let S be the pink area and let 5k be the area of ABC. S(((3k)/2) + S) = (k − S)(((3k)/2)−S) S = ((3k)/8) ((Pink)/(Area of ABC)) = (((3k)/8)/(5k)) = (3/(40))

$${Let}\:{S}\:{be}\:{the}\:{pink}\:{area}\:{and}\:{let}\:\mathrm{5}{k}\:{be}\:{the}\:{area} \\ $$$$\:{of}\:{ABC}. \\ $$$$\:{S}\left(\frac{\mathrm{3}{k}}{\mathrm{2}}\:+\:{S}\right)\:=\:\left({k}\:−\:{S}\right)\left(\frac{\mathrm{3}{k}}{\mathrm{2}}−{S}\right) \\ $$$$\:{S}\:\:=\:\frac{\mathrm{3}{k}}{\mathrm{8}} \\ $$$$\:\frac{{Pink}}{{Area}\:{of}\:{ABC}}\:=\:\frac{\frac{\mathrm{3}{k}}{\mathrm{8}}}{\mathrm{5}{k}}\:=\:\frac{\mathrm{3}}{\mathrm{40}}\:\: \\ $$

Commented by HeferH last updated on 30/Jan/23

Answered by mr W last updated on 30/Jan/23

Commented by mr W last updated on 30/Jan/23

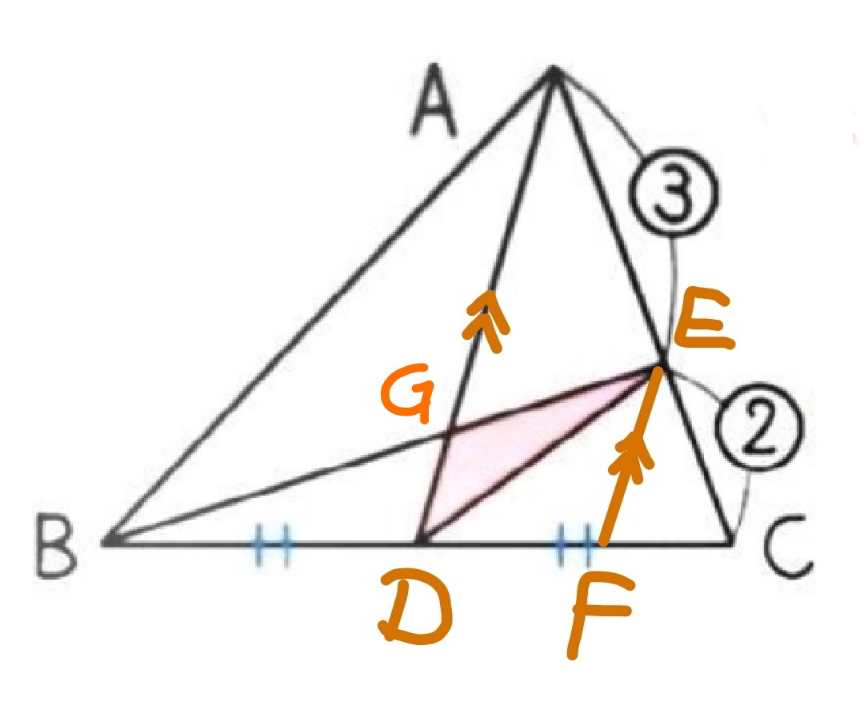
DF=(3/5)×DC=(3/5)×BD GE=(3/5)×BG=(3/8)×BE [GDE]=(3/8)×[BED] =(3/8)×(1/2)×[BEC] =(3/8)×(1/2)×(2/5)×[ABC] =(3/(40))×[ABC] ✓

$${DF}=\frac{\mathrm{3}}{\mathrm{5}}×{DC}=\frac{\mathrm{3}}{\mathrm{5}}×{BD} \\ $$$${GE}=\frac{\mathrm{3}}{\mathrm{5}}×{BG}=\frac{\mathrm{3}}{\mathrm{8}}×{BE} \\ $$$$\left[{GDE}\right]=\frac{\mathrm{3}}{\mathrm{8}}×\left[{BED}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{2}}×\left[{BEC}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{5}}×\left[{ABC}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{40}}×\left[{ABC}\right]\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com