
Question Number 18593 by Joel577 last updated on 25/Jul/17
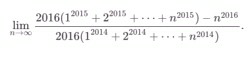
Answered by 433 last updated on 25/Jul/17
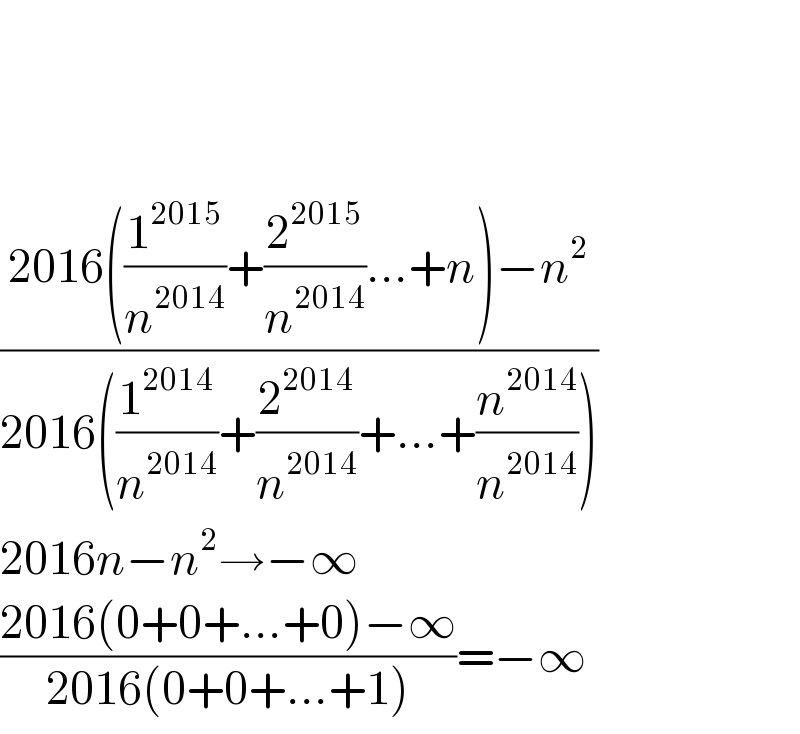
$$ \\ $$$$ \\ $$$$ \\ $$$$\frac{\mathrm{2016}\left(\frac{\mathrm{1}^{\mathrm{2015}} }{{n}^{\mathrm{2014}} }+\frac{\mathrm{2}^{\mathrm{2015}} }{{n}^{\mathrm{2014}} }...+{n}\right)−{n}^{\mathrm{2}} }{\mathrm{2016}\left(\frac{\mathrm{1}^{\mathrm{2014}} }{{n}^{\mathrm{2014}} }+\frac{\mathrm{2}^{\mathrm{2014}} }{{n}^{\mathrm{2014}} }+...+\frac{{n}^{\mathrm{2014}} }{{n}^{\mathrm{2014}} }\right)} \\ $$$$\mathrm{2016}{n}−{n}^{\mathrm{2}} \rightarrow−\infty \\ $$$$\frac{\mathrm{2016}\left(\mathrm{0}+\mathrm{0}+...+\mathrm{0}\right)−\infty}{\mathrm{2016}\left(\mathrm{0}+\mathrm{0}+...+\mathrm{1}\right)}=−\infty \\ $$
