Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 185915 by ajfour last updated on 29/Jan/23

Commented by ajfour last updated on 29/Jan/23

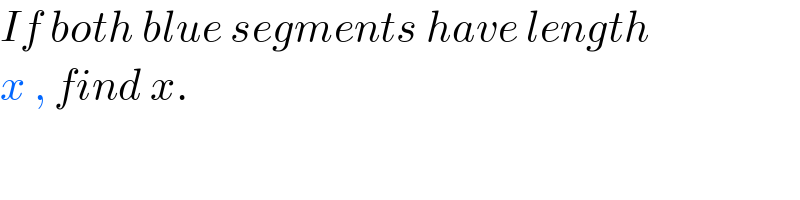
If both blue segments have length x , find x.

$${If}\:{both}\:{blue}\:{segments}\:{have}\:{length} \\ $$$${x}\:,\:{find}\:{x}. \\ $$

Answered by ajfour last updated on 29/Jan/23

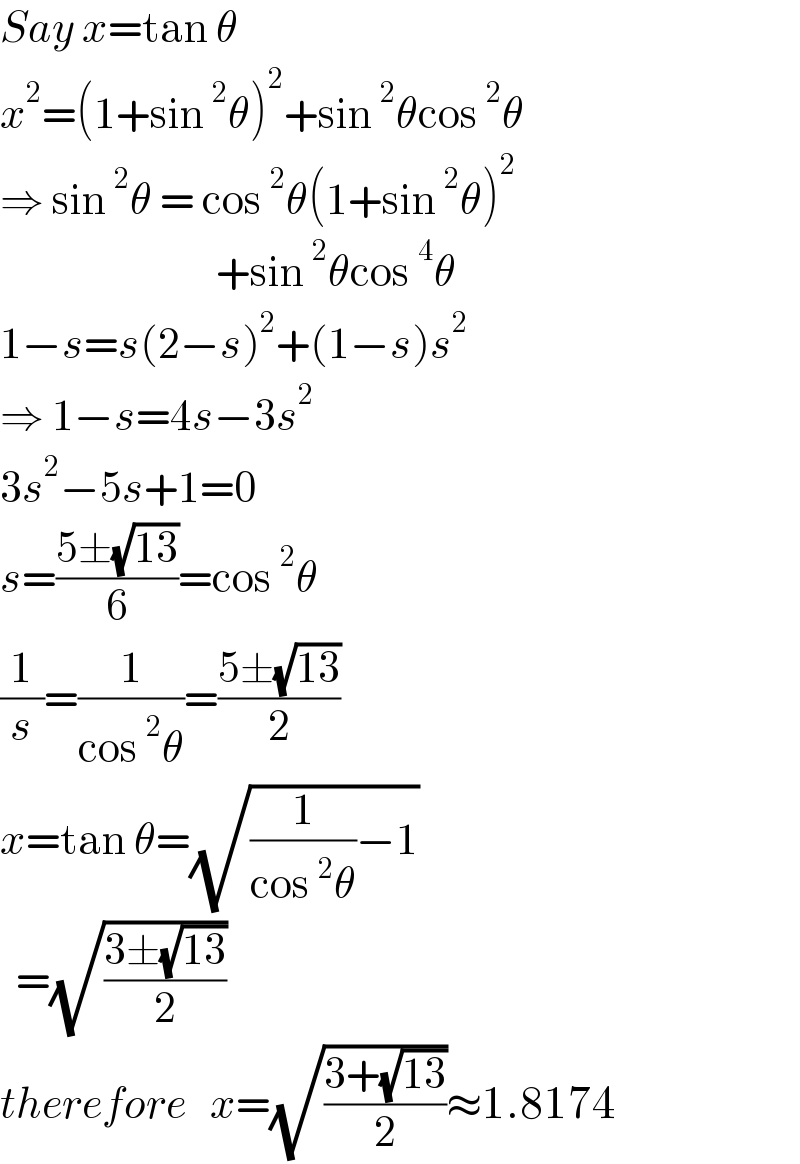
Say x=tan θ x^2 =(1+sin^2 θ)^2 +sin^2 θcos^2 θ ⇒ sin^2 θ = cos^2 θ(1+sin^2 θ)^2 +sin^2 θcos^4 θ 1−s=s(2−s)^2 +(1−s)s^2 ⇒ 1−s=4s−3s^2 3s^2 −5s+1=0 s=((5±(√(13)))/6)=cos^2 θ (1/s)=(1/(cos^2 θ))=((5±(√(13)))/2) x=tan θ=(√((1/(cos^2 θ))−1)) =(√((3±(√(13)))/2)) therefore x=(√((3+(√(13)))/2))≈1.8174

$${Say}\:{x}=\mathrm{tan}\:\theta \\ $$$${x}^{\mathrm{2}} =\left(\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \theta\right)^{\mathrm{2}} +\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:\mathrm{sin}\:^{\mathrm{2}} \theta\:=\:\mathrm{cos}\:^{\mathrm{2}} \theta\left(\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{4}} \theta \\ $$$$\mathrm{1}−{s}={s}\left(\mathrm{2}−{s}\right)^{\mathrm{2}} +\left(\mathrm{1}−{s}\right){s}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{1}−{s}=\mathrm{4}{s}−\mathrm{3}{s}^{\mathrm{2}} \\ $$$$\mathrm{3}{s}^{\mathrm{2}} −\mathrm{5}{s}+\mathrm{1}=\mathrm{0} \\ $$$${s}=\frac{\mathrm{5}\pm\sqrt{\mathrm{13}}}{\mathrm{6}}=\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\frac{\mathrm{1}}{{s}}=\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \theta}=\frac{\mathrm{5}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$${x}=\mathrm{tan}\:\theta=\sqrt{\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \theta}−\mathrm{1}} \\ $$$$\:\:=\sqrt{\frac{\mathrm{3}\pm\sqrt{\mathrm{13}}}{\mathrm{2}}} \\ $$$${therefore}\:\:\:{x}=\sqrt{\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\mathrm{2}}}\approx\mathrm{1}.\mathrm{8174} \\ $$

Commented by ajfour last updated on 29/Jan/23

Answered by mr W last updated on 29/Jan/23

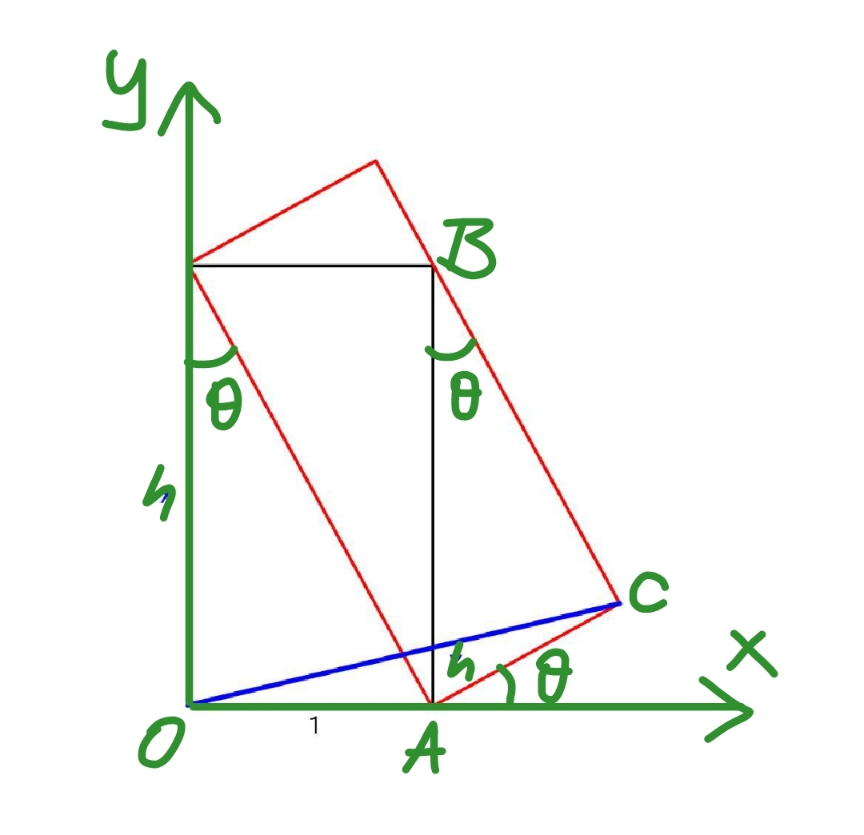
Commented by mr W last updated on 29/Jan/23

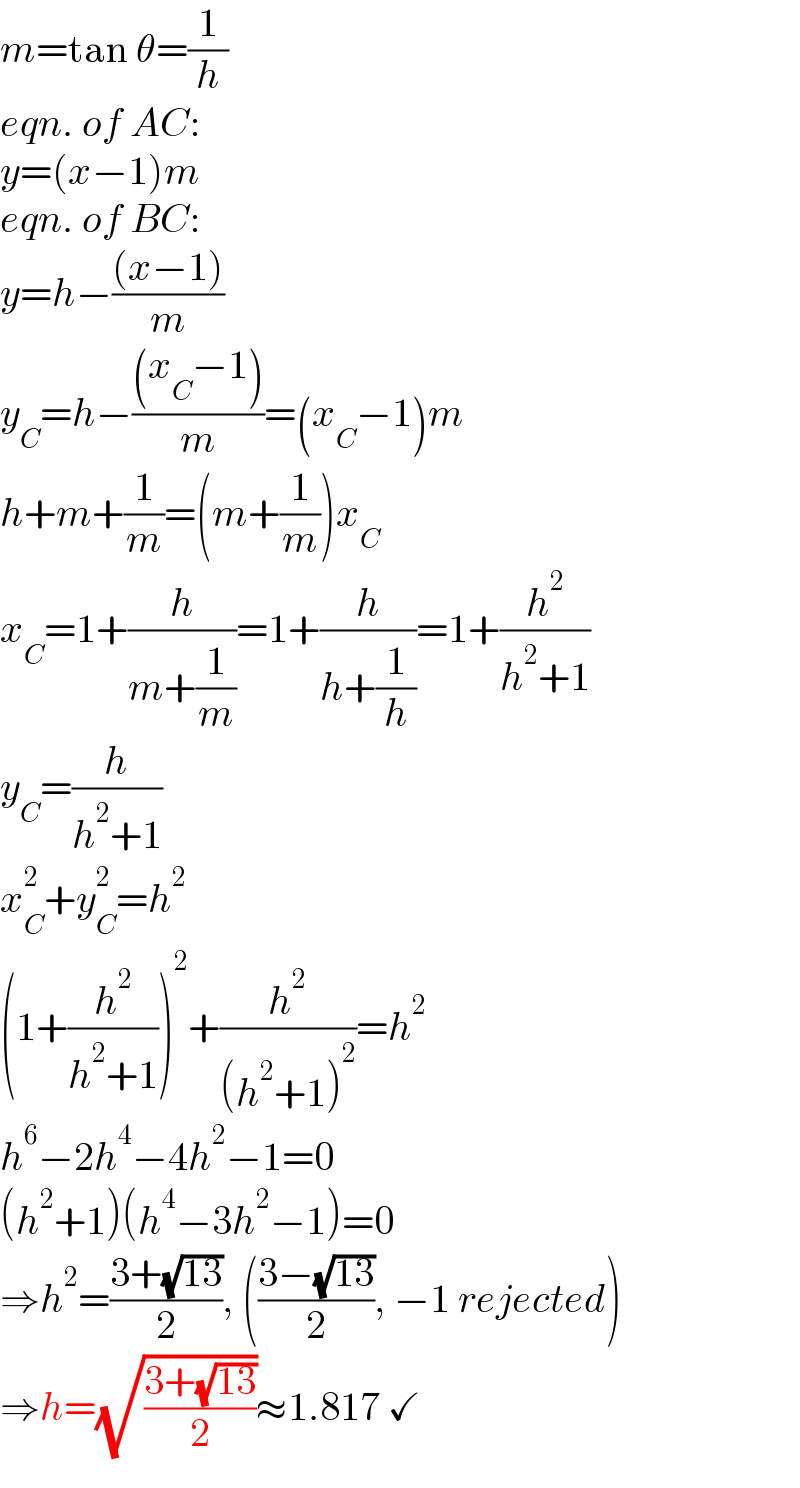
m=tan θ=(1/h) eqn. of AC: y=(x−1)m eqn. of BC: y=h−(((x−1))/m) y_C =h−(((x_C −1))/m)=(x_C −1)m h+m+(1/m)=(m+(1/m))x_C x_C =1+(h/(m+(1/m)))=1+(h/(h+(1/h)))=1+(h^2 /(h^2 +1)) y_C =(h/(h^2 +1)) x_C ^2 +y_C ^2 =h^2 (1+(h^2 /(h^2 +1)))^2 +(h^2 /((h^2 +1)^2 ))=h^2 h^6 −2h^4 −4h^2 −1=0 (h^2 +1)(h^4 −3h^2 −1)=0 ⇒h^2 =((3+(√(13)))/2), (((3−(√(13)))/2), −1 rejected) ⇒h=(√((3+(√(13)))/2))≈1.817 ✓

$${m}=\mathrm{tan}\:\theta=\frac{\mathrm{1}}{{h}} \\ $$$${eqn}.\:{of}\:{AC}: \\ $$$${y}=\left({x}−\mathrm{1}\right){m} \\ $$$${eqn}.\:{of}\:{BC}: \\ $$$${y}={h}−\frac{\left({x}−\mathrm{1}\right)}{{m}} \\ $$$${y}_{{C}} ={h}−\frac{\left({x}_{{C}} −\mathrm{1}\right)}{{m}}=\left({x}_{{C}} −\mathrm{1}\right){m} \\ $$$${h}+{m}+\frac{\mathrm{1}}{{m}}=\left({m}+\frac{\mathrm{1}}{{m}}\right){x}_{{C}} \\ $$$${x}_{{C}} =\mathrm{1}+\frac{{h}}{{m}+\frac{\mathrm{1}}{{m}}}=\mathrm{1}+\frac{{h}}{{h}+\frac{\mathrm{1}}{{h}}}=\mathrm{1}+\frac{{h}^{\mathrm{2}} }{{h}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}_{{C}} =\frac{{h}}{{h}^{\mathrm{2}} +\mathrm{1}} \\ $$$${x}_{{C}} ^{\mathrm{2}} +{y}_{{C}} ^{\mathrm{2}} ={h}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\frac{{h}^{\mathrm{2}} }{{h}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} +\frac{{h}^{\mathrm{2}} }{\left({h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }={h}^{\mathrm{2}} \\ $$$${h}^{\mathrm{6}} −\mathrm{2}{h}^{\mathrm{4}} −\mathrm{4}{h}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left({h}^{\mathrm{2}} +\mathrm{1}\right)\left({h}^{\mathrm{4}} −\mathrm{3}{h}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{h}^{\mathrm{2}} =\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\mathrm{2}},\:\left(\frac{\mathrm{3}−\sqrt{\mathrm{13}}}{\mathrm{2}},\:−\mathrm{1}\:{rejected}\right) \\ $$$$\Rightarrow{h}=\sqrt{\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\mathrm{2}}}\approx\mathrm{1}.\mathrm{817}\:\checkmark \\ $$

Commented by ajfour last updated on 29/Jan/23

Thank you sir.

$${Thank}\:{you}\:{sir}. \\ $$

Answered by HeferH last updated on 29/Jan/23

Commented by HeferH last updated on 29/Jan/23

a = (x^2 /(x^2 + 1)); b = (x/(x^2 + 1)) (1 + (x^2 /(x^2 +1)))^2 +((x/(x^2 +1)))^2 = x^2 (((2x^2 +1)/(x^2 +1)))^2 +((x/(x^2 +1)))^2 = x^2 (2x^2 +1)^2 +x^2 = x^2 (x^2 +1)^2 let x^2 = q 4q^2 +5q + 1 = q(q + 1)^2 (4q + 1)(q + 1) = q(q + 1)^2 q^2 −3q − 1 = 0 q = ((3±(√(13)))/2) ⇒ x = (√((3+(√(13)))/2)) ≈ 1.817

$${a}\:=\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+\:\mathrm{1}};\:{b}\:=\:\frac{{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}} \\ $$$$\:\left(\mathrm{1}\:+\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} \\ $$$$\:\left(\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} \\ $$$$\:\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} =\:{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:{let}\:{x}^{\mathrm{2}} \:=\:{q} \\ $$$$\:\mathrm{4}{q}^{\mathrm{2}} +\mathrm{5}{q}\:+\:\mathrm{1}\:=\:{q}\left({q}\:+\:\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\left(\mathrm{4}{q}\:+\:\mathrm{1}\right)\left({q}\:+\:\mathrm{1}\right)\:=\:{q}\left({q}\:+\:\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:{q}^{\mathrm{2}} −\mathrm{3}{q}\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:{q}\:=\:\frac{\mathrm{3}\pm\sqrt{\mathrm{13}}}{\mathrm{2}}\:\Rightarrow\:{x}\:=\:\sqrt{\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\mathrm{2}}}\:\approx\:\mathrm{1}.\mathrm{817} \\ $$

Commented by ajfour last updated on 29/Jan/23

thanks sir.

$${thanks}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com