
Question Number 185869 by Mingma last updated on 29/Jan/23
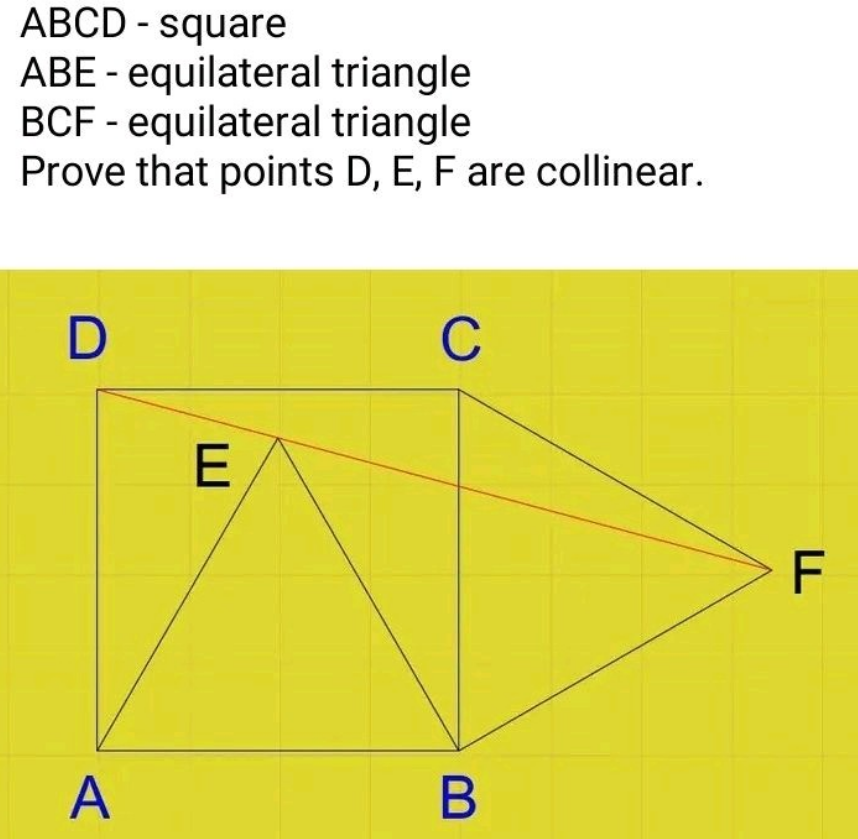
Answered by mr W last updated on 29/Jan/23
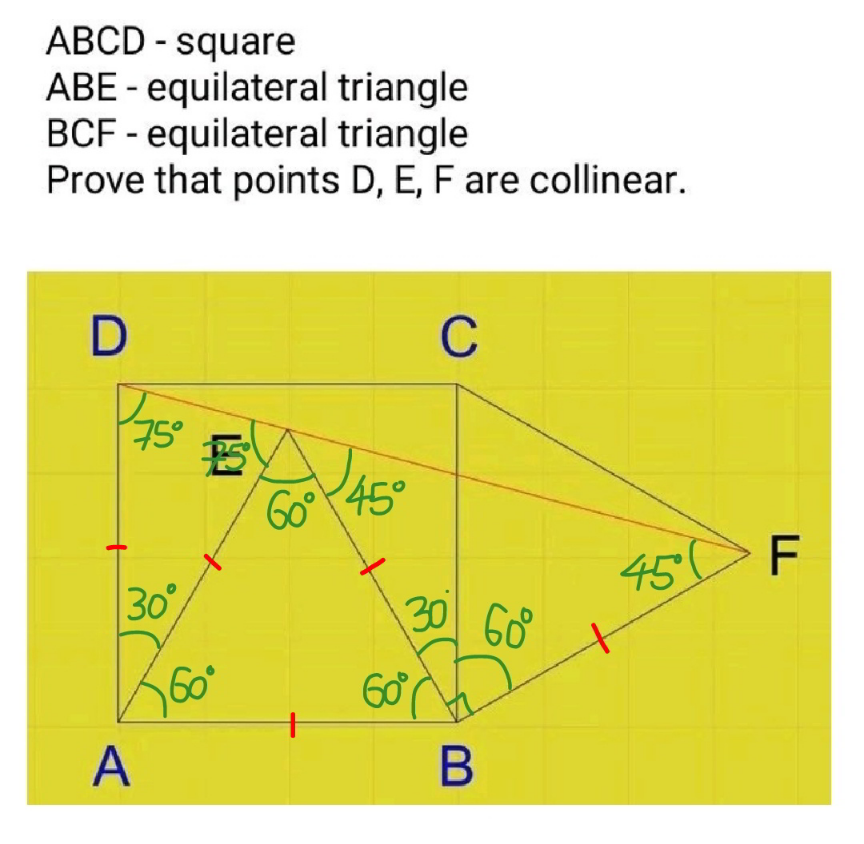
Commented by mr W last updated on 29/Jan/23
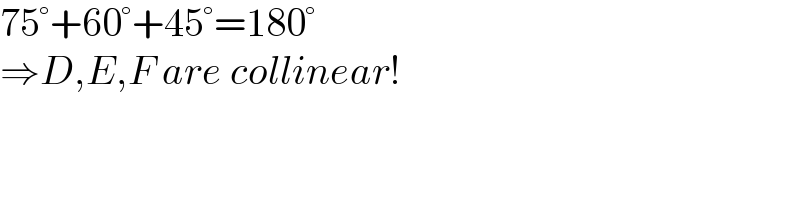
$$\mathrm{75}°+\mathrm{60}°+\mathrm{45}°=\mathrm{180}° \\ $$$$\Rightarrow{D},{E},{F}\:{are}\:{collinear}! \\ $$
Answered by ajfour last updated on 29/Jan/23
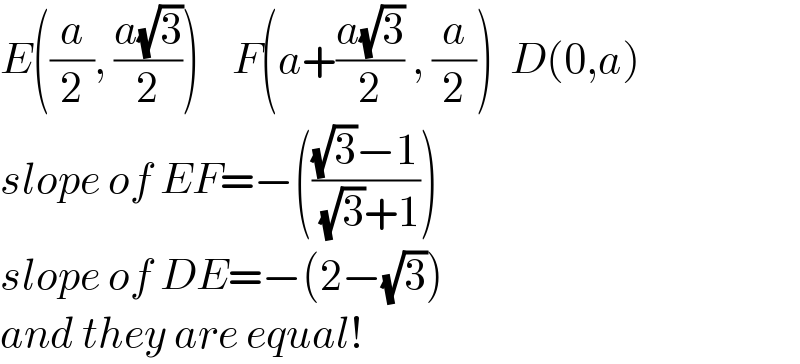
$${E}\left(\frac{{a}}{\mathrm{2}},\:\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\:\:\:{F}\left({a}+\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\:,\:\frac{{a}}{\mathrm{2}}\right)\:\:{D}\left(\mathrm{0},{a}\right) \\ $$$${slope}\:{of}\:{EF}=−\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\right) \\ $$$${slope}\:{of}\:{DE}=−\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$${and}\:{they}\:{are}\:{equal}! \\ $$
