
Question Number 185619 by Mingma last updated on 24/Jan/23
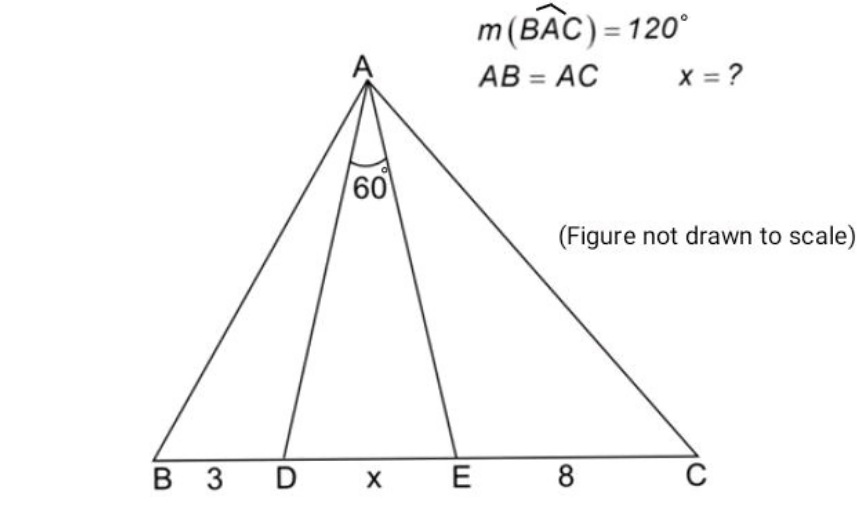
Commented by mr W last updated on 24/Jan/23
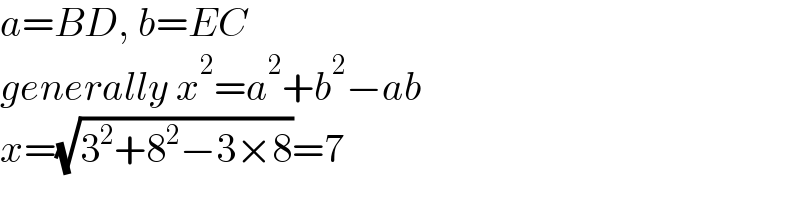
$${a}={BD},\:{b}={EC} \\ $$$${generally}\:{x}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab} \\ $$$${x}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{3}×\mathrm{8}}=\mathrm{7} \\ $$
Answered by mr W last updated on 24/Jan/23
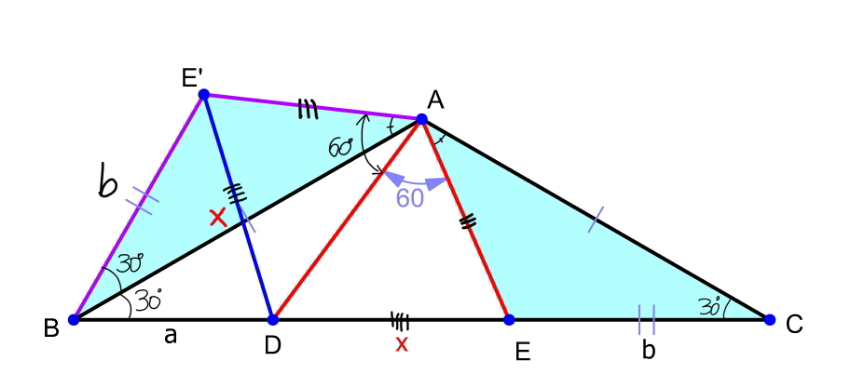
Commented by mr W last updated on 24/Jan/23
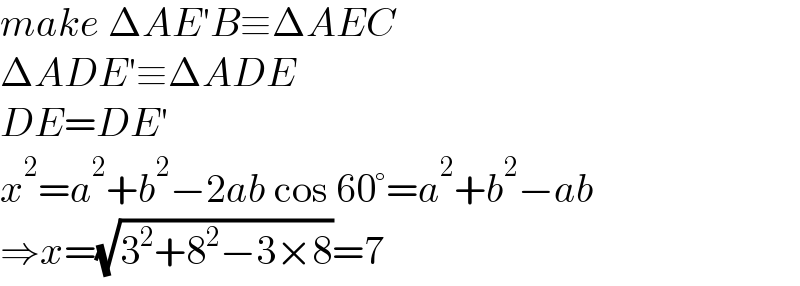
$${make}\:\Delta{AE}'{B}\equiv\Delta{AEC} \\ $$$$\Delta{ADE}'\equiv\Delta{ADE} \\ $$$${DE}={DE}' \\ $$$${x}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\mathrm{60}°={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{3}×\mathrm{8}}=\mathrm{7} \\ $$
