
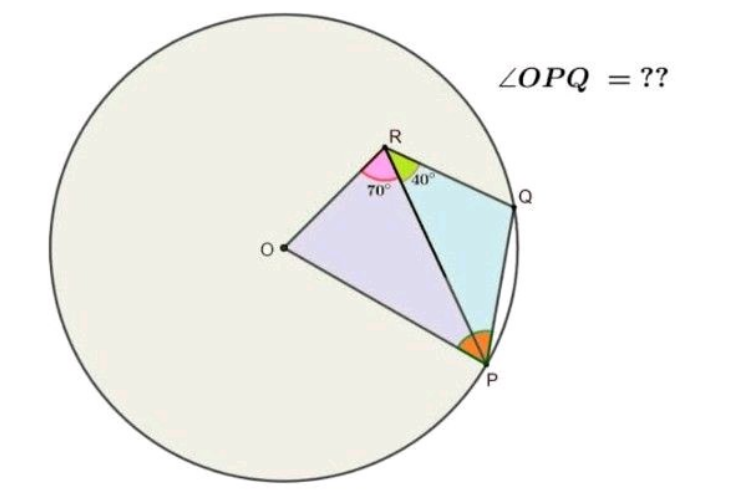
Question Number 185231 by Rupesh123 last updated on 18/Jan/23
Answered by Kalebwizeman last updated on 19/Jan/23

$$\mathrm{70}\:{degrees} \\ $$
Answered by Kalebwizeman last updated on 19/Jan/23

$${draw}\:{a}\:{line}\:{joining}\:{OQ} \\ $$$${angle}\:{POQ}\:{is}\:\mathrm{40}\:\left({same}\:{segment}\right) \\ $$$${and}\:{triangle}\:{POQ}\:{is}\:{isosceles} \\ $$$${so}\:{the}\:{required}\:{angle}\:{just}\:{one}\:{of}\:{the}\:{base}\:{angles} \\ $$
Commented by HeferH last updated on 19/Jan/23

$${but}\:{how}\:{POQ}\:{is}\:\mathrm{40}°\:? \\ $$
Answered by mr W last updated on 20/Jan/23

Commented by mr W last updated on 20/Jan/23
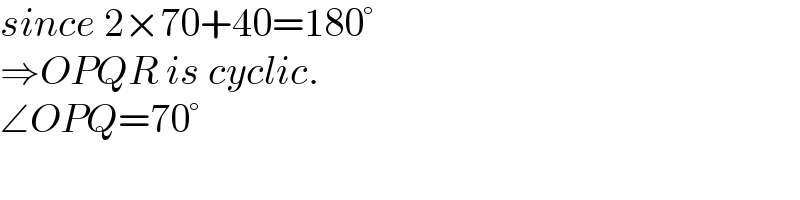
$${since}\:\mathrm{2}×\mathrm{70}+\mathrm{40}=\mathrm{180}° \\ $$$$\Rightarrow{OPQR}\:{is}\:{cyclic}. \\ $$$$\angle{OPQ}=\mathrm{70}° \\ $$
