Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 184481 by yaslm last updated on 07/Jan/23

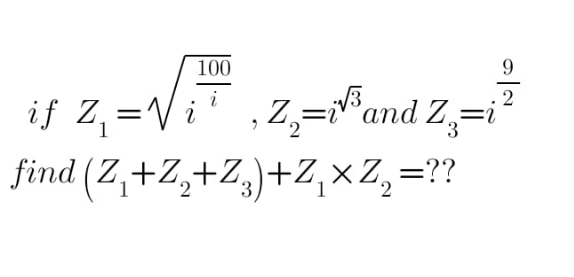
Answered by mahdipoor last updated on 07/Jan/23

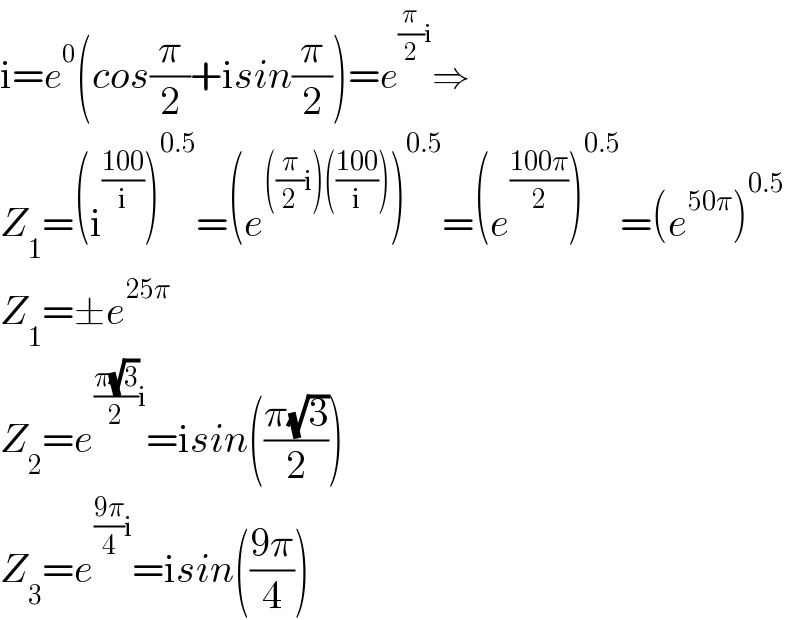
i=e^0 (cos(π/2)+isin(π/2))=e^((π/2)i) ⇒ Z_1 =(i^((100)/i) )^(0.5) =(e^(((π/2)i)(((100)/i))) )^(0.5) =(e^((100π)/2) )^(0.5) =(e^(50π) )^(0.5) Z_1 =±e^(25π) Z_2 =e^(((π(√3))/2)i) =isin(((π(√3))/2)) Z_3 =e^(((9π)/4)i) =isin(((9π)/4))

$$\mathrm{i}={e}^{\mathrm{0}} \left({cos}\frac{\pi}{\mathrm{2}}+\mathrm{i}{sin}\frac{\pi}{\mathrm{2}}\right)={e}^{\frac{\pi}{\mathrm{2}}\mathrm{i}} \Rightarrow \\ $$$${Z}_{\mathrm{1}} =\left(\mathrm{i}^{\frac{\mathrm{100}}{\mathrm{i}}} \right)^{\mathrm{0}.\mathrm{5}} =\left({e}^{\left(\frac{\pi}{\mathrm{2}}\mathrm{i}\right)\left(\frac{\mathrm{100}}{\mathrm{i}}\right)} \right)^{\mathrm{0}.\mathrm{5}} =\left({e}^{\frac{\mathrm{100}\pi}{\mathrm{2}}} \right)^{\mathrm{0}.\mathrm{5}} =\left({e}^{\mathrm{50}\pi} \right)^{\mathrm{0}.\mathrm{5}} \\ $$$${Z}_{\mathrm{1}} =\pm{e}^{\mathrm{25}\pi} \:\:\:\:\: \\ $$$${Z}_{\mathrm{2}} ={e}^{\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}} =\mathrm{i}{sin}\left(\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${Z}_{\mathrm{3}} ={e}^{\frac{\mathrm{9}\pi}{\mathrm{4}}\mathrm{i}} =\mathrm{i}{sin}\left(\frac{\mathrm{9}\pi}{\mathrm{4}}\right) \\ $$

Commented by yaslm last updated on 07/Jan/23

thanks complete sir

Commented by Frix last updated on 07/Jan/23

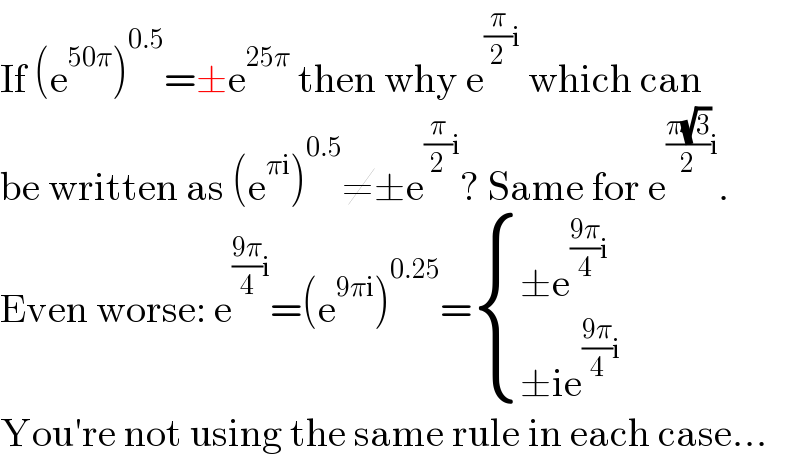
If (e^(50π) )^(0.5) =±e^(25π) then why e^((π/2)i) which can be written as (e^(πi) )^(0.5) ≠±e^((π/2)i) ? Same for e^(((π(√3))/2)i) . Even worse: e^(((9π)/4)i) =(e^(9πi) )^(0.25) = { ((±e^(((9π)/4)i) )),((±ie^(((9π)/4)i) )) :} You′re not using the same rule in each case...

$$\mathrm{If}\:\left(\mathrm{e}^{\mathrm{50}\pi} \right)^{\mathrm{0}.\mathrm{5}} =\pm\mathrm{e}^{\mathrm{25}\pi} \:\mathrm{then}\:\mathrm{why}\:\mathrm{e}^{\frac{\pi}{\mathrm{2}}\mathrm{i}} \:\mathrm{which}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{written}\:\mathrm{as}\:\left(\mathrm{e}^{\pi\mathrm{i}} \right)^{\mathrm{0}.\mathrm{5}} \neq\pm\mathrm{e}^{\frac{\pi}{\mathrm{2}}\mathrm{i}} ?\:\mathrm{Same}\:\mathrm{for}\:\mathrm{e}^{\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}} . \\ $$$$\mathrm{Even}\:\mathrm{worse}:\:\mathrm{e}^{\frac{\mathrm{9}\pi}{\mathrm{4}}\mathrm{i}} =\left(\mathrm{e}^{\mathrm{9}\pi\mathrm{i}} \right)^{\mathrm{0}.\mathrm{25}} =\begin{cases}{\pm\mathrm{e}^{\frac{\mathrm{9}\pi}{\mathrm{4}}\mathrm{i}} }\\{\pm\mathrm{ie}^{\frac{\mathrm{9}\pi}{\mathrm{4}}\mathrm{i}} }\end{cases} \\ $$$$\mathrm{You}'\mathrm{re}\:\mathrm{not}\:\mathrm{using}\:\mathrm{the}\:\mathrm{same}\:\mathrm{rule}\:\mathrm{in}\:\mathrm{each}\:\mathrm{case}... \\ $$

Answered by Frix last updated on 07/Jan/23

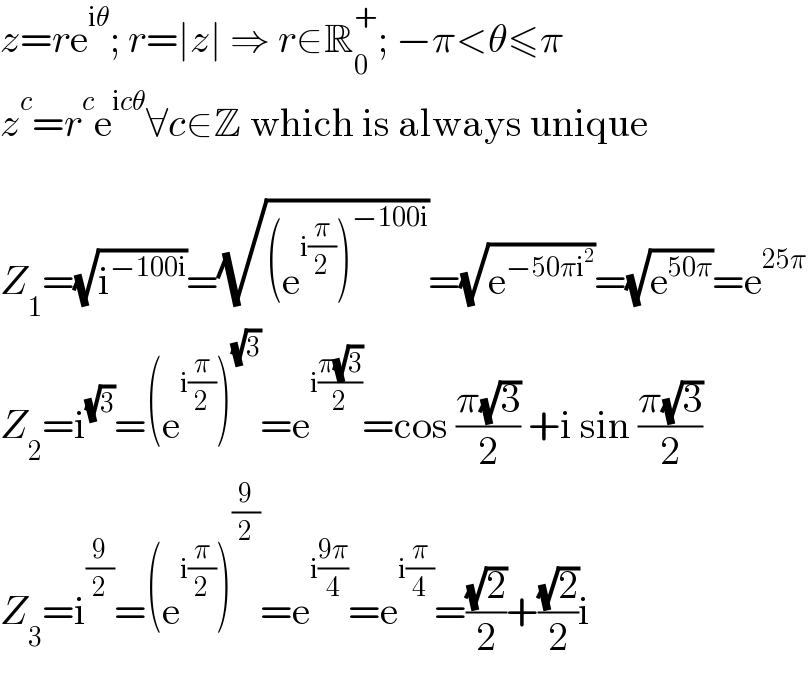
z=re^(iθ) ; r=∣z∣ ⇒ r∈R_0 ^+ ; −π<θ≤π z^c =r^c e^(icθ) ∀c∈Z which is always unique Z_1 =(√i^(−100i) )=(√((e^(i(π/2)) )^(−100i) ))=(√e^(−50πi^2 ) )=(√e^(50π) )=e^(25π) Z_2 =i^(√3) =(e^(i(π/2)) )^(√3) =e^(i((π(√3))/2)) =cos ((π(√3))/2) +i sin ((π(√3))/2) Z_3 =i^(9/2) =(e^(i(π/2)) )^(9/2) =e^(i((9π)/4)) =e^(i(π/4)) =((√2)/2)+((√2)/2)i

$${z}={r}\mathrm{e}^{\mathrm{i}\theta} ;\:{r}=\mid{z}\mid\:\Rightarrow\:{r}\in\mathbb{R}_{\mathrm{0}} ^{+} ;\:−\pi<\theta\leqslant\pi \\ $$$${z}^{{c}} ={r}^{{c}} \mathrm{e}^{\mathrm{i}{c}\theta} \forall{c}\in\mathbb{Z}\:\mathrm{which}\:\mathrm{is}\:\mathrm{always}\:\mathrm{unique} \\ $$$$ \\ $$$${Z}_{\mathrm{1}} =\sqrt{\mathrm{i}^{−\mathrm{100i}} }=\sqrt{\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} \right)^{−\mathrm{100i}} }=\sqrt{\mathrm{e}^{−\mathrm{50}\pi\mathrm{i}^{\mathrm{2}} } }=\sqrt{\mathrm{e}^{\mathrm{50}\pi} }=\mathrm{e}^{\mathrm{25}\pi} \\ $$$${Z}_{\mathrm{2}} =\mathrm{i}^{\sqrt{\mathrm{3}}} =\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} \right)^{\sqrt{\mathrm{3}}} =\mathrm{e}^{\mathrm{i}\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}}} =\mathrm{cos}\:\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}}\:+\mathrm{i}\:\mathrm{sin}\:\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${Z}_{\mathrm{3}} =\mathrm{i}^{\frac{\mathrm{9}}{\mathrm{2}}} =\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{9}}{\mathrm{2}}} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{9}\pi}{\mathrm{4}}} =\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com