
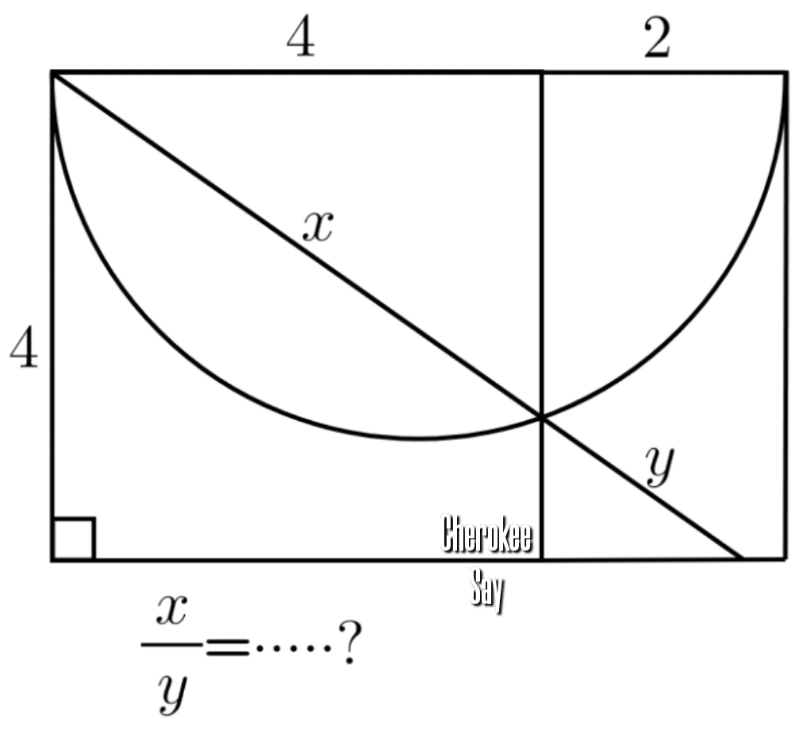
Question Number 184352 by cherokeesay last updated on 05/Jan/23
Answered by som(math1967) last updated on 05/Jan/23
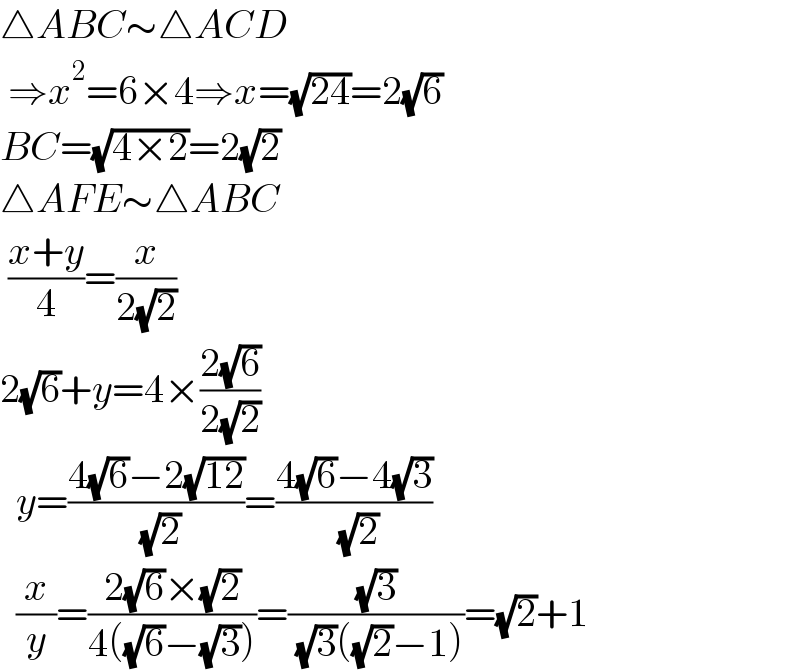
$$\bigtriangleup{ABC}\sim\bigtriangleup{ACD} \\ $$$$\:\Rightarrow{x}^{\mathrm{2}} =\mathrm{6}×\mathrm{4}\Rightarrow{x}=\sqrt{\mathrm{24}}=\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${BC}=\sqrt{\mathrm{4}×\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\bigtriangleup{AFE}\sim\bigtriangleup{ABC} \\ $$$$\:\frac{{x}+{y}}{\mathrm{4}}=\frac{{x}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{2}\sqrt{\mathrm{6}}+{y}=\mathrm{4}×\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\:\:{y}=\frac{\mathrm{4}\sqrt{\mathrm{6}}−\mathrm{2}\sqrt{\mathrm{12}}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{4}\sqrt{\mathrm{6}}−\mathrm{4}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\:\frac{{x}}{{y}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}×\sqrt{\mathrm{2}}}{\mathrm{4}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}\right)}=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}=\sqrt{\mathrm{2}}+\mathrm{1} \\ $$
Commented by som(math1967) last updated on 05/Jan/23
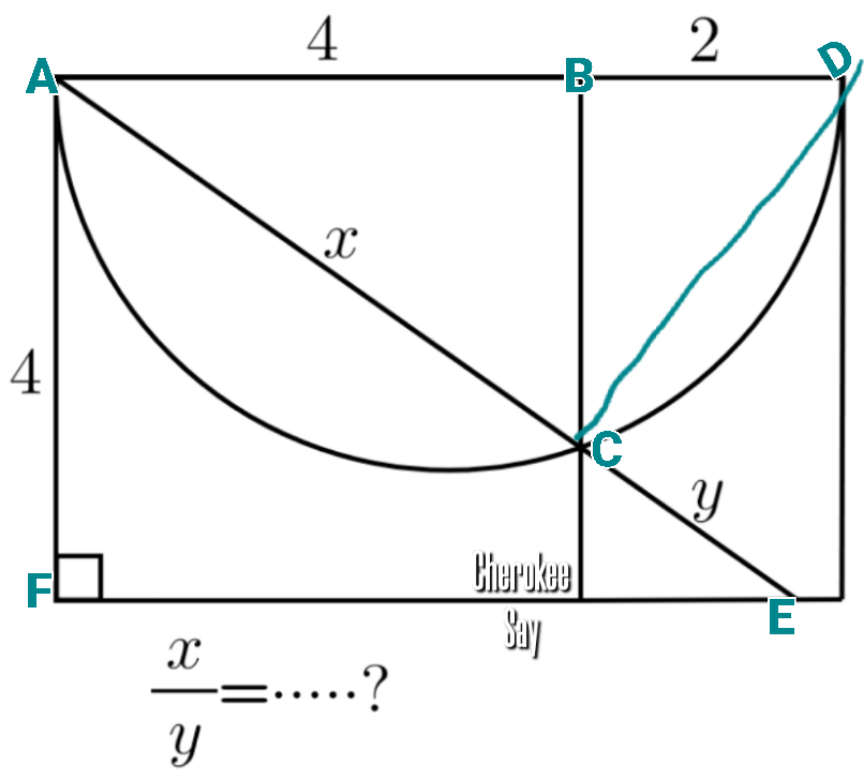
Commented by cherokeesay last updated on 05/Jan/23
$${nice}\:!\:{thank}\:{you}\:{sir}. \\ $$
Answered by mr W last updated on 05/Jan/23
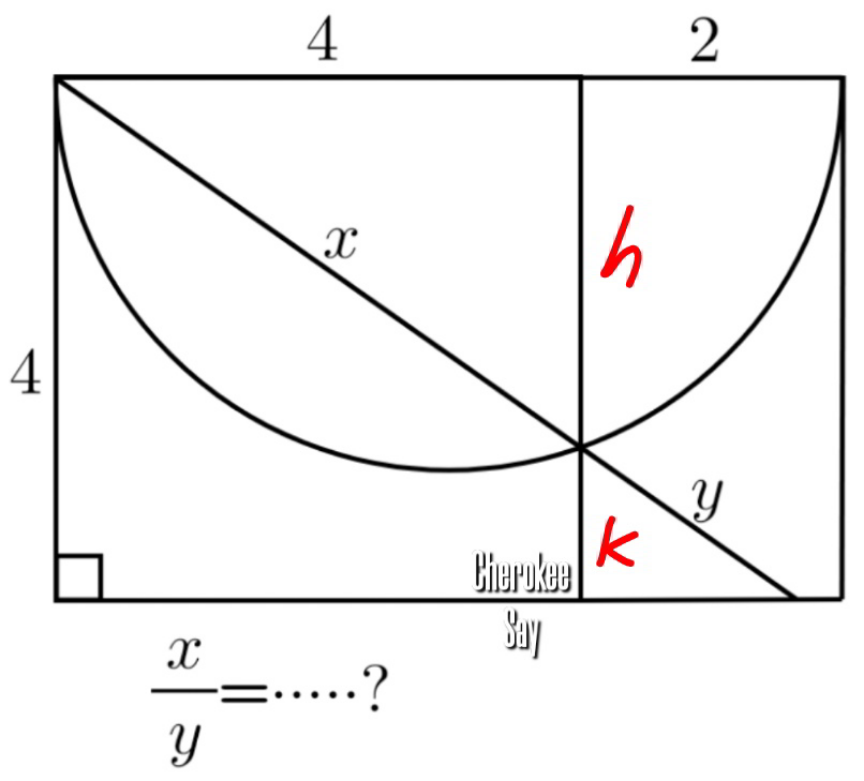
Commented by mr W last updated on 05/Jan/23
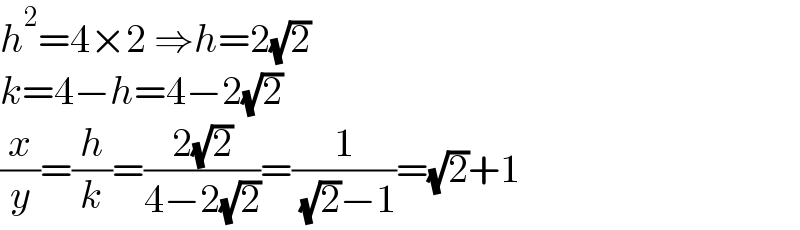
$${h}^{\mathrm{2}} =\mathrm{4}×\mathrm{2}\:\Rightarrow{h}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${k}=\mathrm{4}−{h}=\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\frac{{x}}{{y}}=\frac{{h}}{{k}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\sqrt{\mathrm{2}}+\mathrm{1} \\ $$
Commented by cherokeesay last updated on 05/Jan/23

$${thank}\:{you}\:{sir}. \\ $$
Answered by HeferH last updated on 05/Jan/23
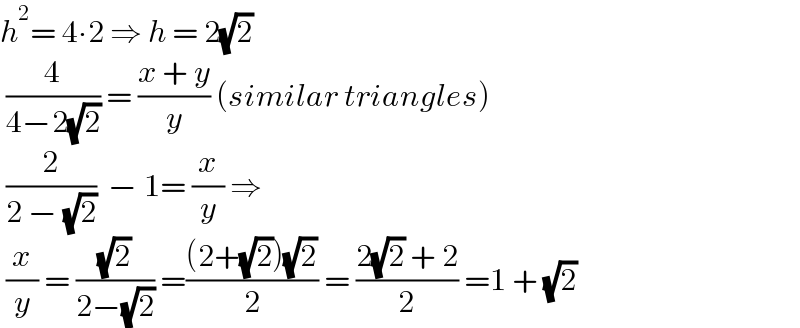
$${h}^{\mathrm{2}} =\:\mathrm{4}\centerdot\mathrm{2}\:\Rightarrow\:{h}\:=\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:\frac{\mathrm{4}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}\:=\:\frac{{x}\:+\:{y}}{{y}}\:\left({similar}\:{triangles}\right) \\ $$$$\:\frac{\mathrm{2}}{\mathrm{2}\:−\:\sqrt{\mathrm{2}}}\:\:−\:\mathrm{1}=\:\frac{{x}}{{y}}\:\Rightarrow\: \\ $$$$\:\frac{{x}}{{y}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}\:=\frac{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}\:+\:\mathrm{2}}{\mathrm{2}}\:=\mathrm{1}\:+\:\sqrt{\mathrm{2}}\: \\ $$
