Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 184240 by ajfour last updated on 04/Jan/23

Commented by ajfour last updated on 04/Jan/23

Find largest r given b.

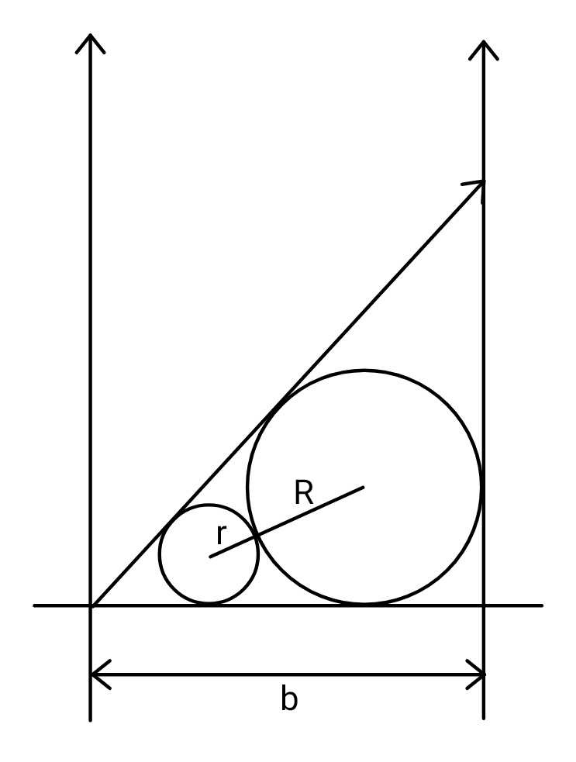
$${Find}\:{largest}\:{r}\:{given}\:{b}. \\ $$

Answered by mr W last updated on 04/Jan/23

Commented by mr W last updated on 04/Jan/23

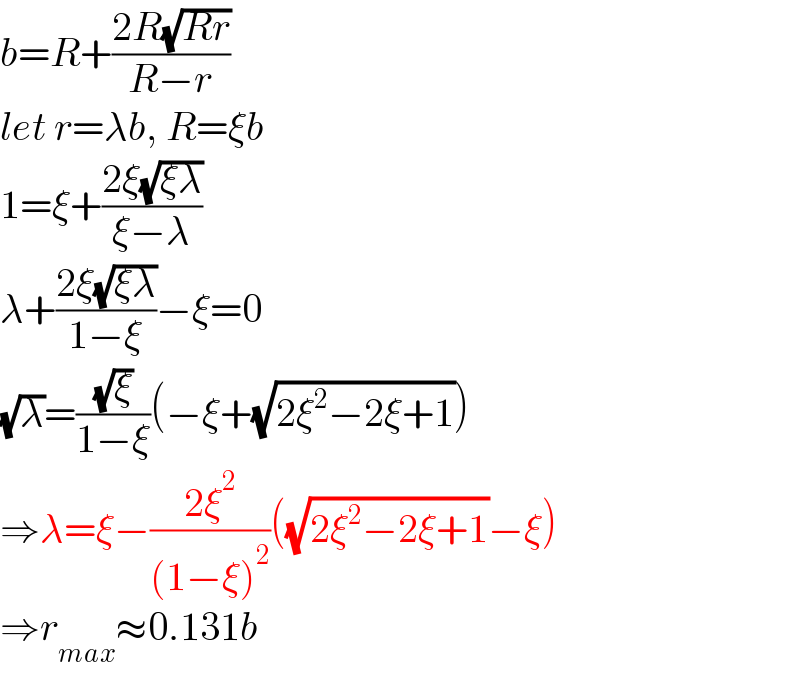
b=R+((2R(√(Rr)))/(R−r)) let r=λb, R=ξb 1=ξ+((2ξ(√(ξλ)))/(ξ−λ)) λ+((2ξ(√(ξλ)))/(1−ξ))−ξ=0 (√λ)=((√ξ)/(1−ξ))(−ξ+(√(2ξ^2 −2ξ+1))) ⇒λ=ξ−((2ξ^2 )/((1−ξ)^2 ))((√(2ξ^2 −2ξ+1))−ξ) ⇒r_(max) ≈0.131b

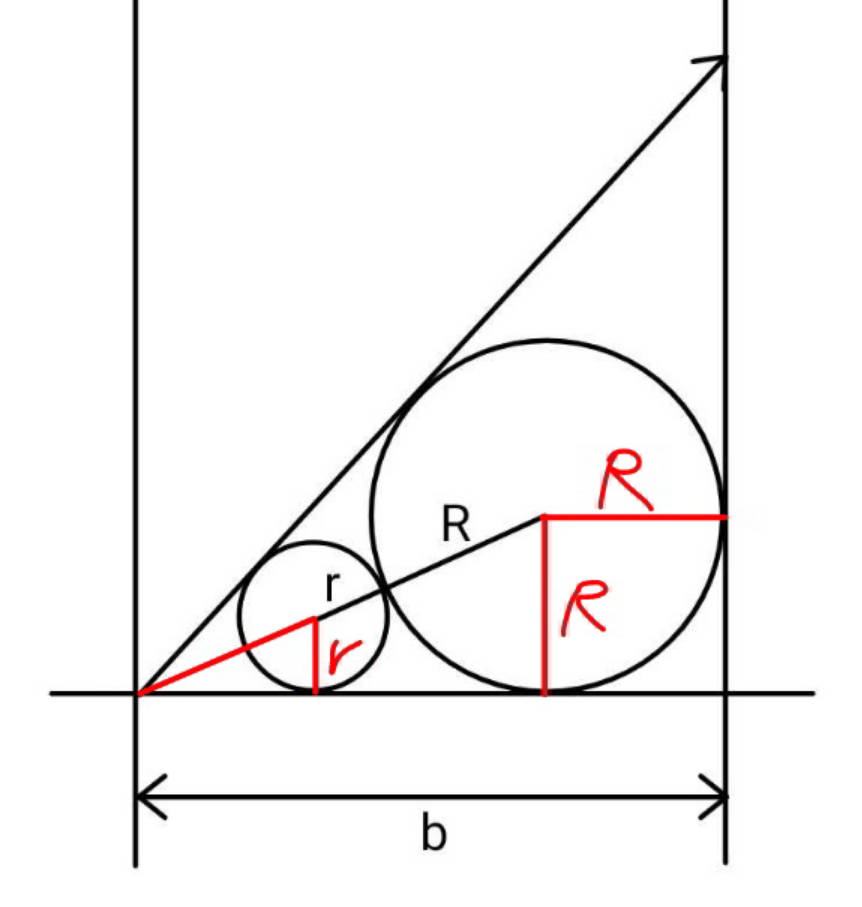
$${b}={R}+\frac{\mathrm{2}{R}\sqrt{{Rr}}}{{R}−{r}} \\ $$$${let}\:{r}=\lambda{b},\:{R}=\xi{b} \\ $$$$\mathrm{1}=\xi+\frac{\mathrm{2}\xi\sqrt{\xi\lambda}}{\xi−\lambda} \\ $$$$\lambda+\frac{\mathrm{2}\xi\sqrt{\xi\lambda}}{\mathrm{1}−\xi}−\xi=\mathrm{0} \\ $$$$\sqrt{\lambda}=\frac{\sqrt{\xi}}{\mathrm{1}−\xi}\left(−\xi+\sqrt{\mathrm{2}\xi^{\mathrm{2}} −\mathrm{2}\xi+\mathrm{1}}\right) \\ $$$$\Rightarrow\lambda=\xi−\frac{\mathrm{2}\xi^{\mathrm{2}} }{\left(\mathrm{1}−\xi\right)^{\mathrm{2}} }\left(\sqrt{\mathrm{2}\xi^{\mathrm{2}} −\mathrm{2}\xi+\mathrm{1}}−\xi\right) \\ $$$$\Rightarrow{r}_{{max}} \approx\mathrm{0}.\mathrm{131}{b} \\ $$

Commented by mr W last updated on 04/Jan/23

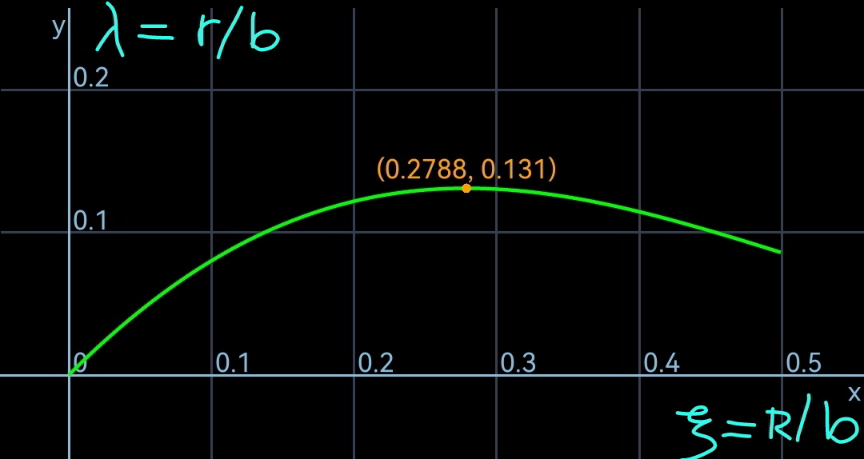
Answered by ajfour last updated on 04/Jan/23

cos 2θ=((R−r)/(R+r)) ⇒ r=R(((1−cos 2θ)/(1+cos 2θ)))=Rtan^2 θ b=rtan 2θ+2(√(Rr))+R say tan θ=m b=R(((2m^3 )/(1−m^2 ))+2m+1) r=((bm^2 )/(((2m^3 )/(1−m^2 ))+2m+1))=((bm^2 (m^2 −1))/(m^2 −2m−1)) ⇒ (r/b) =((m^2 (m−(1/m)))/(m−(1/m)−2)) r_(max) =0.13103b (dr/dm)=0 ⇒ [2m(m−(1/m))+m^2 (1+(1/m^2 ))](m−(1/m)−2) =m^2 (m−(1/m))(1+(1/m^2 )) ⇒ (3m^2 −1)(m−(1/m)−2) =(m^2 +1)(m−(1/m)) or 1−(2/((m−(1/m))))=((m^2 +1)/(3(m^2 −(1/3)))) ⇒ (m^2 −1)(m−(1/m))=(3m^2 −1) ⇒ (m^2 −1)^2 =m(3m^2 −1) ⇒ m≈0.6855

$$\mathrm{cos}\:\mathrm{2}\theta=\frac{{R}−{r}}{{R}+{r}} \\ $$$$\Rightarrow\:\:{r}={R}\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}\right)={R}\mathrm{tan}\:^{\mathrm{2}} \theta \\ $$$${b}={r}\mathrm{tan}\:\mathrm{2}\theta+\mathrm{2}\sqrt{{Rr}}+{R} \\ $$$${say}\:\:\mathrm{tan}\:\theta={m} \\ $$$$\:\:{b}={R}\left(\frac{\mathrm{2}{m}^{\mathrm{3}} }{\mathrm{1}−{m}^{\mathrm{2}} }+\mathrm{2}{m}+\mathrm{1}\right) \\ $$$${r}=\frac{{bm}^{\mathrm{2}} }{\frac{\mathrm{2}{m}^{\mathrm{3}} }{\mathrm{1}−{m}^{\mathrm{2}} }+\mathrm{2}{m}+\mathrm{1}}=\frac{{bm}^{\mathrm{2}} \left({m}^{\mathrm{2}} −\mathrm{1}\right)}{{m}^{\mathrm{2}} −\mathrm{2}{m}−\mathrm{1}} \\ $$$$\Rightarrow\:\frac{{r}}{{b}}\:=\frac{{m}^{\mathrm{2}} \left({m}−\frac{\mathrm{1}}{{m}}\right)}{{m}−\frac{\mathrm{1}}{{m}}−\mathrm{2}} \\ $$$$\:\:\:{r}_{{max}} =\mathrm{0}.\mathrm{13103}{b} \\ $$$$\frac{{dr}}{{dm}}=\mathrm{0}\:\:\Rightarrow \\ $$$$\left[\mathrm{2}{m}\left({m}−\frac{\mathrm{1}}{{m}}\right)+{m}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right)\right]\left({m}−\frac{\mathrm{1}}{{m}}−\mathrm{2}\right) \\ $$$$\:\:\:={m}^{\mathrm{2}} \left({m}−\frac{\mathrm{1}}{{m}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\left(\mathrm{3}{m}^{\mathrm{2}} −\mathrm{1}\right)\left({m}−\frac{\mathrm{1}}{{m}}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left({m}^{\mathrm{2}} +\mathrm{1}\right)\left({m}−\frac{\mathrm{1}}{{m}}\right) \\ $$$${or}\:\:\:\:\mathrm{1}−\frac{\mathrm{2}}{\left({m}−\frac{\mathrm{1}}{{m}}\right)}=\frac{{m}^{\mathrm{2}} +\mathrm{1}}{\mathrm{3}\left({m}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)} \\ $$$$\Rightarrow\:\:\left({m}^{\mathrm{2}} −\mathrm{1}\right)\left({m}−\frac{\mathrm{1}}{{m}}\right)=\left(\mathrm{3}{m}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\left({m}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ={m}\left(\mathrm{3}{m}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\Rightarrow\:\:{m}\approx\mathrm{0}.\mathrm{6855} \\ $$$$ \\ $$

Commented by mr W last updated on 04/Jan/23

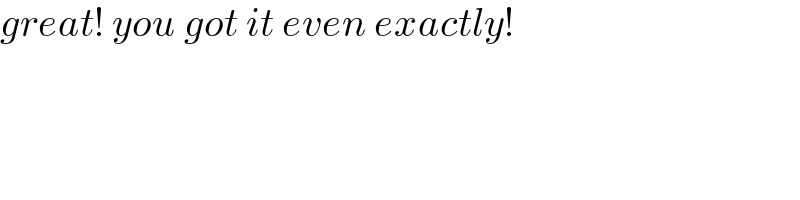
great! you got it even exactly!

$${great}!\:{you}\:{got}\:{it}\:{even}\:{exactly}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com