
Question Number 184121 by Noorzai last updated on 03/Jan/23

Commented by Rasheed.Sindhi last updated on 03/Jan/23

$${See}\:{Q}#\mathrm{182423} \\ $$$${Why}\:{have}\:{you}\:{repeated}\:{your}\:\boldsymbol{{own}} \\ $$$$\boldsymbol{{answered}}\:{question}? \\ $$
Commented by mr W last updated on 03/Jan/23

$${because}\:{he}\:{actually}\:{is}\:{not}\:{interested} \\ $$$${in}\:{the}\:{solution}\:{of}\:{the}\:{question}\:{and} \\ $$$${also}\:{doesn}'{t}\:{really}\:{want}\:{to}\:{learn}\:{from}\: \\ $$$${the}\:{solution},\:{maybe}\:{even}\:{doesn}'{t}\:{read}\: \\ $$$${it}.\:{he}\:{posts}\:{a}\:{question}\:{just}\:{in}\:{order} \\ $$$${to}\:{post}\:{a}\:{question}.\:{next}\:{time}\:{when}\:{he} \\ $$$${sees}\:{this}\:{question}\:{somewhere}\:{else}, \\ $$$${he}\:{will}\:{post}\:{it}\:{again}. \\ $$$${there}\:{are}\:{some}\:{users}\:{of}\:{this}\:{kind}\:{in} \\ $$$${this}\:{forum}.\:{they}\:{appear}\:{here},\:{post} \\ $$$${some}\:{questions},\:{then}\:{disappear}\:{and} \\ $$$${don}'{t}\:{given}\:{any}\:{response}\:{to}\:{the}\: \\ $$$${answers}\:{of}\:{their}\:{own}\:{questions}. \\ $$$${you}\:{may}\:{recognize}\:{such}\:{people},\:{because} \\ $$$${they}\:{never}\:{communicate}\:{with}\:{you}, \\ $$$${when}\:{you}\:{answer}\:{their}\:{questions}. \\ $$$${you}\:{even}\:{don}'{t}\:{know}\:{if}\:{they}\:{read}\:{your} \\ $$$${answers}\:{at}\:{all}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jan/23
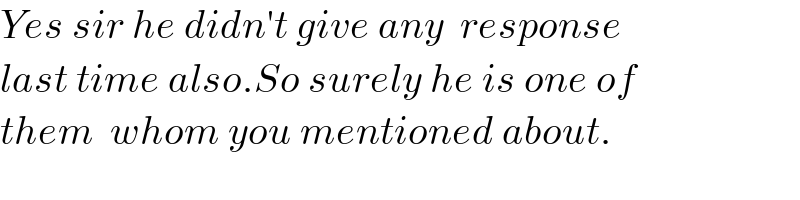
$${Yes}\:{sir}\:{he}\:{didn}'{t}\:{give}\:{any}\:\:{response} \\ $$$${last}\:{time}\:{also}.{So}\:{surely}\:{he}\:{is}\:{one}\:{of} \\ $$$${them}\:\:{whom}\:{you}\:{mentioned}\:{about}. \\ $$
Commented by SEKRET last updated on 03/Jan/23

$$\:\:\boldsymbol{\mathrm{maybe}}\:\:\boldsymbol{\mathrm{not}}\:\:\boldsymbol{\mathrm{well}}\:\:\boldsymbol{\mathrm{understood}} \\ $$
Answered by Rasheed.Sindhi last updated on 03/Jan/23
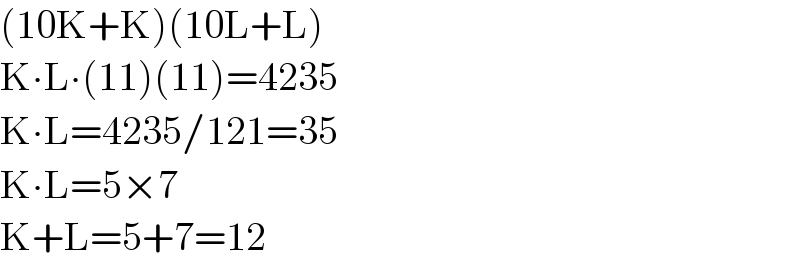
$$\left(\mathrm{10K}+\mathrm{K}\right)\left(\mathrm{10L}+\mathrm{L}\right) \\ $$$$\mathrm{K}\centerdot\mathrm{L}\centerdot\left(\mathrm{11}\right)\left(\mathrm{11}\right)=\mathrm{4235} \\ $$$$\mathrm{K}\centerdot\mathrm{L}=\mathrm{4235}/\mathrm{121}=\mathrm{35} \\ $$$$\mathrm{K}\centerdot\mathrm{L}=\mathrm{5}×\mathrm{7} \\ $$$$\mathrm{K}+\mathrm{L}=\mathrm{5}+\mathrm{7}=\mathrm{12} \\ $$
Commented by Noorzai last updated on 03/Jan/23
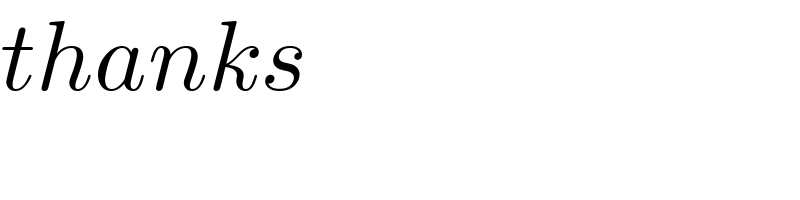
$${thanks} \\ $$
Answered by manolex last updated on 03/Jan/23
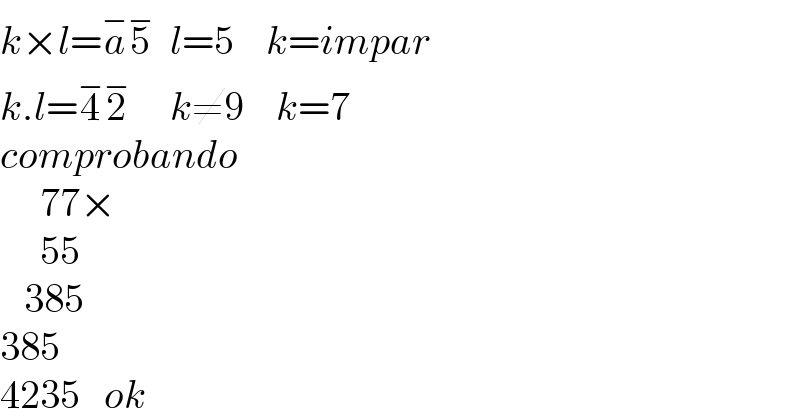
$${k}×{l}=\overset{−} {{a}}\overset{−} {\mathrm{5}}\:\:{l}=\mathrm{5}\:\:\:\:{k}={impar} \\ $$$${k}.{l}=\overset{−} {\mathrm{4}}\overset{−} {\mathrm{2}}\:\:\:\:\:{k}\neq\mathrm{9}\:\:\:\:{k}=\mathrm{7}\:\: \\ $$$${comprobando} \\ $$$$\:\:\:\:\:\mathrm{77}× \\ $$$$\:\:\:\:\:\mathrm{55} \\ $$$$\:\:\:\mathrm{385} \\ $$$$\mathrm{385} \\ $$$$\mathrm{4235}\:\:\:{ok} \\ $$
