
Question Number 184041 by Acem last updated on 02/Jan/23
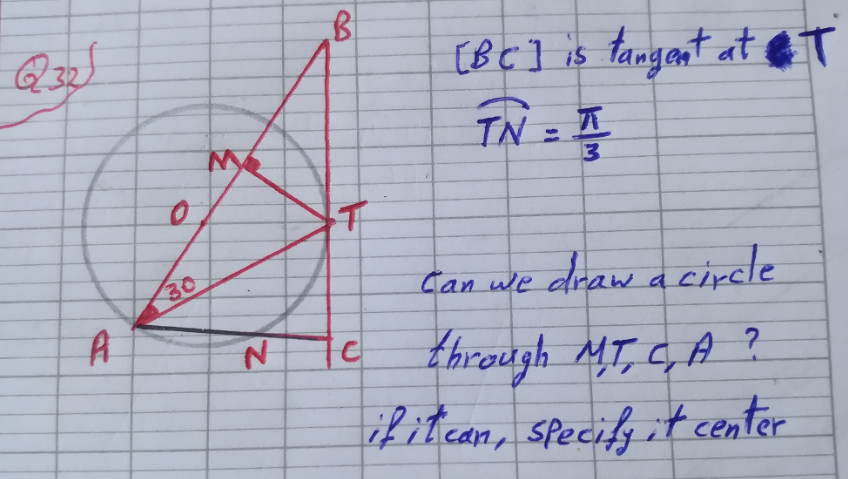
Answered by HeferH last updated on 02/Jan/23

$$\overset{\frown} {{TN}}\:=\:\frac{\pi}{\mathrm{3}}\:=\:\frac{\mathrm{180}°}{\mathrm{3}}\:=\:\mathrm{60}°\:\:\Rightarrow\:\angle{TAN}\:=\:\frac{\overset{\frown} {{TN}}}{\mathrm{2}}\:=\:\mathrm{30}° \\ $$$$\:\angle{AOT}\:=\:\mathrm{120}°\:\left(\bigtriangleup{AOT}\:{isosceles}\right)\: \\ $$$$\:\angle{ATC}\:=\:\frac{\overset{\frown} {{AT}}}{\mathrm{2}}\:=\:\mathrm{60}\:\:\Rightarrow\:\angle{ACT}\:=\:\mathrm{90}°\: \\ $$$$\:{MTCA}\:{is}\:{cyclic}, \\ $$$$\:{the}\:{center}\:{would}\:{be}\:{the}\:{mid}\:{point}\:{of}\:{AT} \\ $$
Answered by mr W last updated on 02/Jan/23
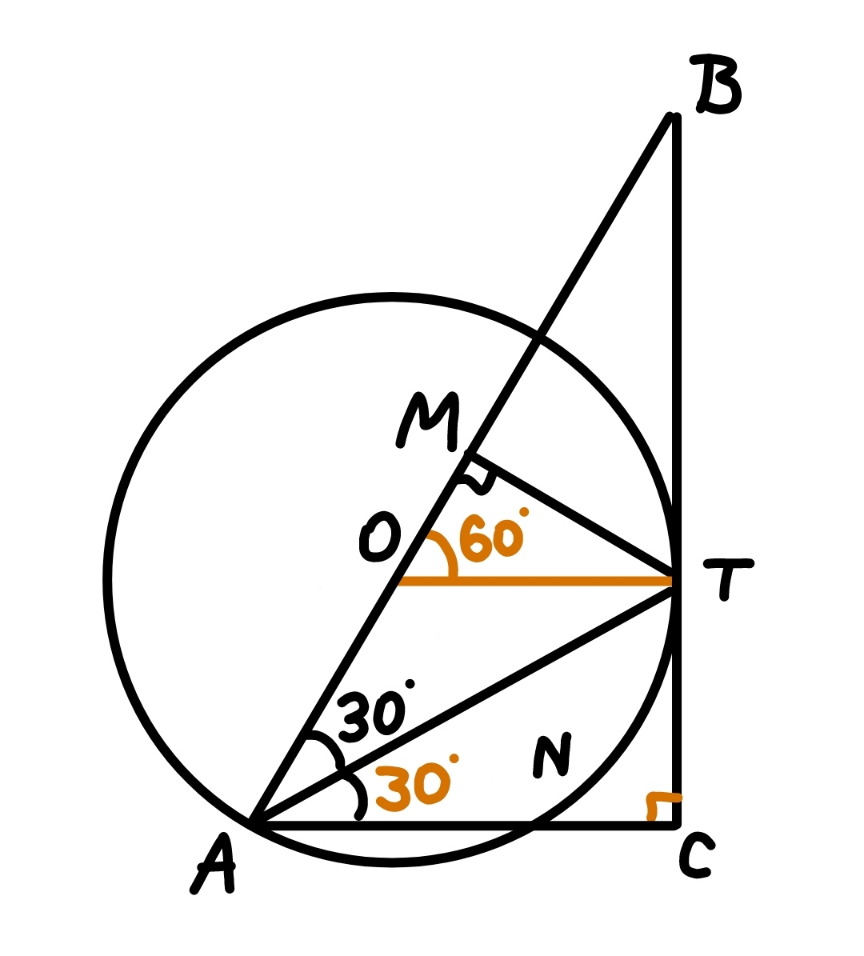
Commented by mr W last updated on 02/Jan/23

$$\angle{TAN}=\frac{\overset{\frown} {{TN}}}{\mathrm{2}}=\mathrm{30}° \\ $$$$\angle{BOT}=\mathrm{2}\angle{OAT}=\mathrm{60}°=\angle{OAC} \\ $$$$\Rightarrow{AC}//{OT} \\ $$$$\Rightarrow{AC}\bot{BC} \\ $$$$\Rightarrow\angle{ACB}=\mathrm{90}°=\angle{AMT} \\ $$$$\Rightarrow{ACTM}\:{are}\:{cyclic},\:{lie}\:{on}\:{a}\:{circle} \\ $$$$\:\:\:\:\:{with}\:{AT}\:{as}\:{diameter}.\:{Midpoint} \\ $$$$\:\:\:\:\:{of}\:{AT}\:{is}\:{the}\:{center}. \\ $$
