
Question Number 183962 by Acem last updated on 01/Jan/23
Commented by Acem last updated on 01/Jan/23
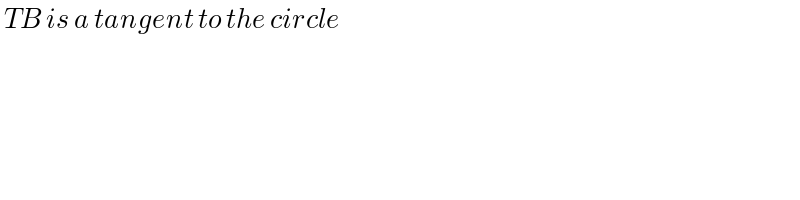
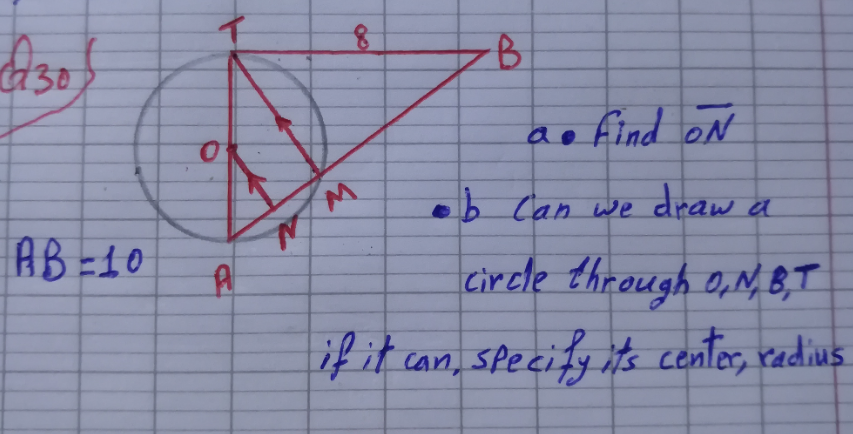
$$\:{TB}\:{is}\:{a}\:{tangent}\:{to}\:{the}\:{circle} \\ $$
Answered by mr W last updated on 01/Jan/23

$$\left({a}\right) \\ $$$$\frac{\sqrt{\mathrm{8}^{\mathrm{2}} −{TM}^{\mathrm{2}} }}{\mathrm{8}}=\frac{\mathrm{8}}{\mathrm{10}} \\ $$$$\Rightarrow{TM}=\frac{\mathrm{24}}{\mathrm{5}} \\ $$$${ON}=\frac{{TM}}{\mathrm{2}}=\frac{\mathrm{12}}{\mathrm{5}} \\ $$$$\left({b}\right) \\ $$$${yes},\:{with}\:{OB}\:{as}\:{diameter}\:{and} \\ $$$${center}\:{at}\:{midpoint}\:{of}\:{OB}. \\ $$$${radius}\:{r}=\frac{{OB}}{\mathrm{2}}=\frac{\sqrt{\mathrm{8}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\sqrt{\mathrm{73}}}{\mathrm{2}} \\ $$
Commented by Acem last updated on 02/Jan/23

$${Thanks}\:{Sir}! \\ $$
Answered by Acem last updated on 02/Jan/23

