Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 183847 by Michaelfaraday last updated on 30/Dec/22

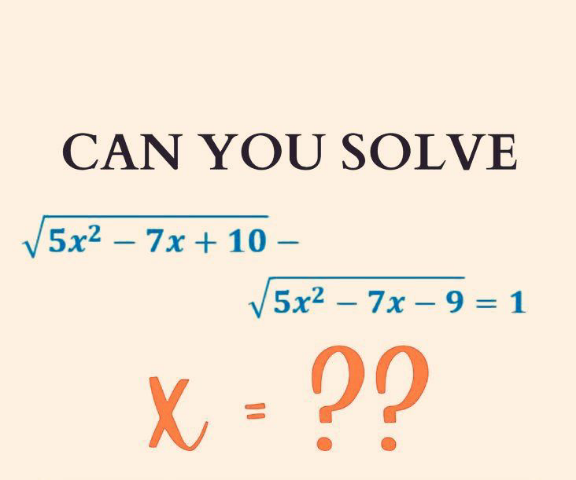
Answered by MJS_new last updated on 31/Dec/22

5x^2 −7x=t (√(t+10))−(√(t−9))=1 (√(100))−(√(81))=1 t=90 x=−((18)/5)∨x=5

$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}={t} \\ $$$$\sqrt{{t}+\mathrm{10}}−\sqrt{{t}−\mathrm{9}}=\mathrm{1} \\ $$$$\sqrt{\mathrm{100}}−\sqrt{\mathrm{81}}=\mathrm{1} \\ $$$${t}=\mathrm{90} \\ $$$${x}=−\frac{\mathrm{18}}{\mathrm{5}}\vee{x}=\mathrm{5} \\ $$

Commented by Michaelfaraday last updated on 31/Dec/22

thanks sir

$${thanks}\:{sir} \\ $$

Commented by MJS_new last updated on 31/Dec/22

sometimes you need sharp eyes instead of sharp brains

$$\mathrm{sometimes}\:\mathrm{you}\:\mathrm{need}\:\mathrm{sharp}\:\mathrm{eyes}\:\mathrm{instead}\:\mathrm{of} \\ $$$$\mathrm{sharp}\:\mathrm{brains} \\ $$

Answered by a.lgnaoui last updated on 31/Dec/22

(√(5x^2 −7x+10)) −(√((5x^2 −7x+10)−19)) )^2 =1 5x^2 −7x+10=z z+(z−19)−2(√(z(z−19)) =1 (√(z(z−19))) =10−z z(z−19)=100+z^2 −20z 100−z=0⇒z=100 5x^2 −7x−90=0 △=49+20×90=1849=43^2 x=((7±43)/(10)) x=5 x_1 =5 verification (√(125−35+10)) −(√(125−35−9)) =10−9=1

$$\left.\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}}\:−\sqrt{\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}\right)−\mathrm{19}}\:\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}={z} \\ $$$${z}+\left({z}−\mathrm{19}\right)−\mathrm{2}\sqrt{{z}\left({z}−\mathrm{19}\right.}\:=\mathrm{1} \\ $$$$\:\sqrt{{z}\left({z}−\mathrm{19}\right)}\:=\mathrm{10}−{z} \\ $$$$\:{z}\left({z}−\mathrm{19}\right)=\mathrm{100}+{z}^{\mathrm{2}} −\mathrm{20}{z} \\ $$$$\mathrm{100}−{z}=\mathrm{0}\Rightarrow{z}=\mathrm{100} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{90}=\mathrm{0} \\ $$$$\bigtriangleup=\mathrm{49}+\mathrm{20}×\mathrm{90}=\mathrm{1849}=\mathrm{43}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:{x}=\frac{\mathrm{7}\pm\mathrm{43}}{\mathrm{10}}\:\:\:\:\:{x}=\mathrm{5} \\ $$$${x}_{\mathrm{1}} =\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:{verification} \\ $$$$\sqrt{\mathrm{125}−\mathrm{35}+\mathrm{10}}\:−\sqrt{\mathrm{125}−\mathrm{35}−\mathrm{9}}\:=\mathrm{10}−\mathrm{9}=\mathrm{1} \\ $$$$ \\ $$

Commented by Michaelfaraday last updated on 31/Dec/22

thanks sir

$${thanks}\:{sir} \\ $$

Answered by mr W last updated on 31/Dec/22

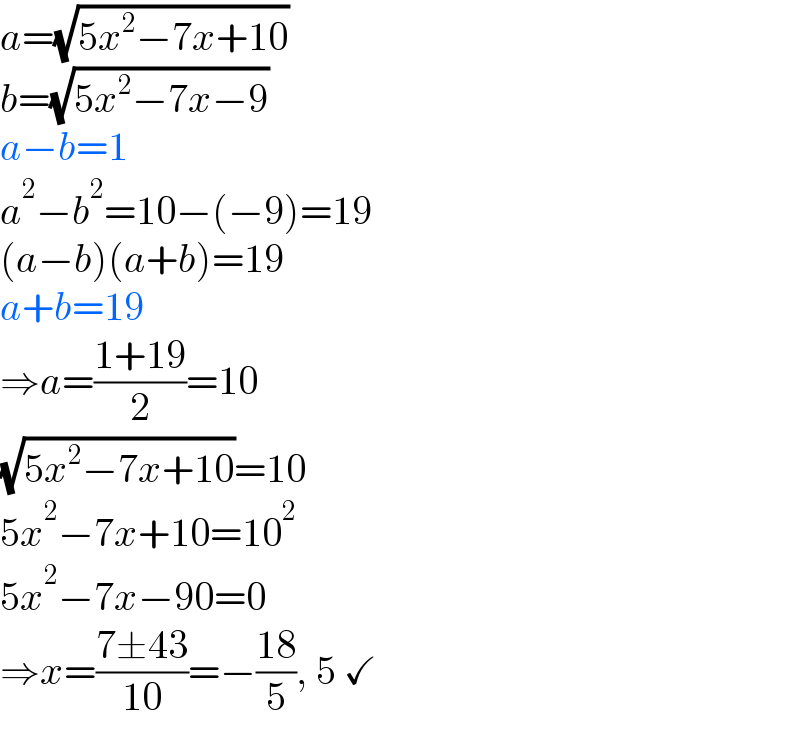
a=(√(5x^2 −7x+10)) b=(√(5x^2 −7x−9)) a−b=1 a^2 −b^2 =10−(−9)=19 (a−b)(a+b)=19 a+b=19 ⇒a=((1+19)/2)=10 (√(5x^2 −7x+10))=10 5x^2 −7x+10=10^2 5x^2 −7x−90=0 ⇒x=((7±43)/(10))=−((18)/5), 5 ✓

$${a}=\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}} \\ $$$${b}=\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{9}} \\ $$$${a}−{b}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{10}−\left(−\mathrm{9}\right)=\mathrm{19} \\ $$$$\left({a}−{b}\right)\left({a}+{b}\right)=\mathrm{19} \\ $$$${a}+{b}=\mathrm{19} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}+\mathrm{19}}{\mathrm{2}}=\mathrm{10} \\ $$$$\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}}=\mathrm{10} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}=\mathrm{10}^{\mathrm{2}} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{90}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{7}\pm\mathrm{43}}{\mathrm{10}}=−\frac{\mathrm{18}}{\mathrm{5}},\:\mathrm{5}\:\checkmark \\ $$

Commented by Michaelfaraday last updated on 31/Dec/22

wow,thanks sir

$${wow},{thanks}\:{sir} \\ $$

Answered by manxsol last updated on 31/Dec/22

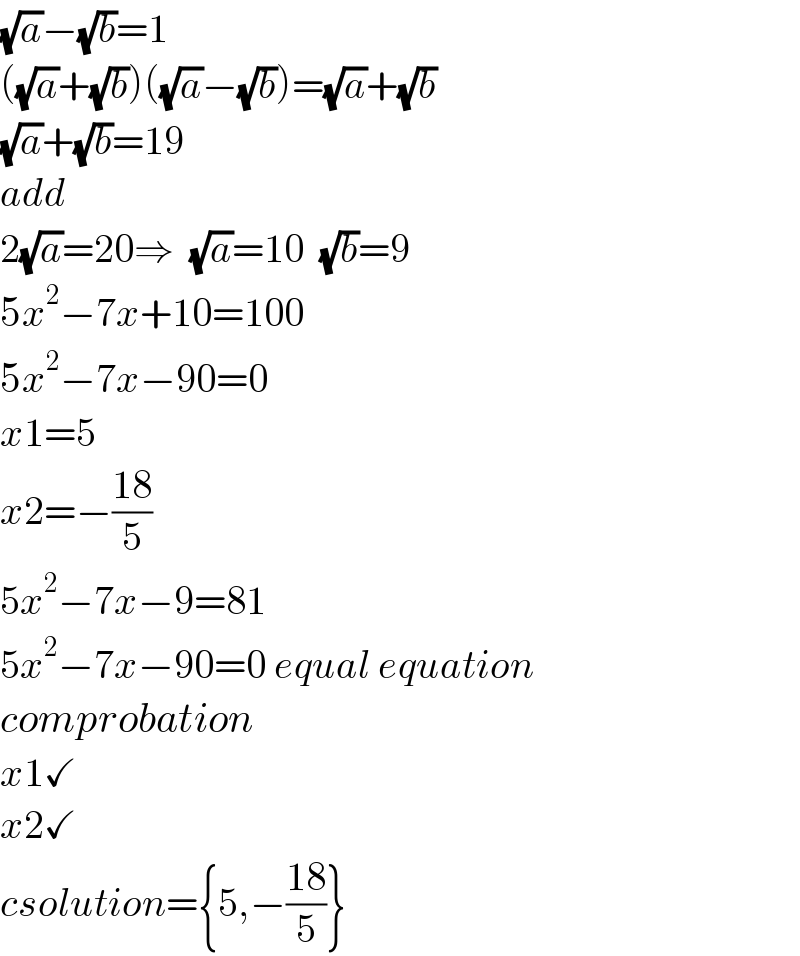
(√a)−(√b)=1 ((√a)+(√b))((√a)−(√b))=(√a)+(√b) (√a)+(√b)=19 add 2(√a)=20⇒ (√a)=10 (√b)=9 5x^2 −7x+10=100 5x^2 −7x−90=0 x1=5 x2=−((18)/5) 5x^2 −7x−9=81 5x^2 −7x−90=0 equal equation comprobation x1✓ x2✓ csolution={5,−((18)/5)}

$$\sqrt{{a}}−\sqrt{{b}}=\mathrm{1} \\ $$$$\left(\sqrt{{a}}+\sqrt{{b}}\right)\left(\sqrt{{a}}−\sqrt{{b}}\right)=\sqrt{{a}}+\sqrt{{b}} \\ $$$$\sqrt{{a}}+\sqrt{{b}}=\mathrm{19} \\ $$$${add} \\ $$$$\mathrm{2}\sqrt{{a}}=\mathrm{20}\Rightarrow\:\:\sqrt{{a}}=\mathrm{10}\:\:\sqrt{{b}}=\mathrm{9} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}=\mathrm{100} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{90}=\mathrm{0} \\ $$$${x}\mathrm{1}=\mathrm{5} \\ $$$${x}\mathrm{2}=−\frac{\mathrm{18}}{\mathrm{5}} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{9}=\mathrm{81} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{90}=\mathrm{0}\:{equal}\:{equation} \\ $$$${comprobation} \\ $$$${x}\mathrm{1}\checkmark \\ $$$${x}\mathrm{2}\checkmark \\ $$$${csolution}=\left\{\mathrm{5},−\frac{\mathrm{18}}{\mathrm{5}}\right\} \\ $$

Commented by Michaelfaraday last updated on 31/Dec/22

thanks sir

$${thanks}\:{sir} \\ $$

Answered by Rasheed.Sindhi last updated on 31/Dec/22

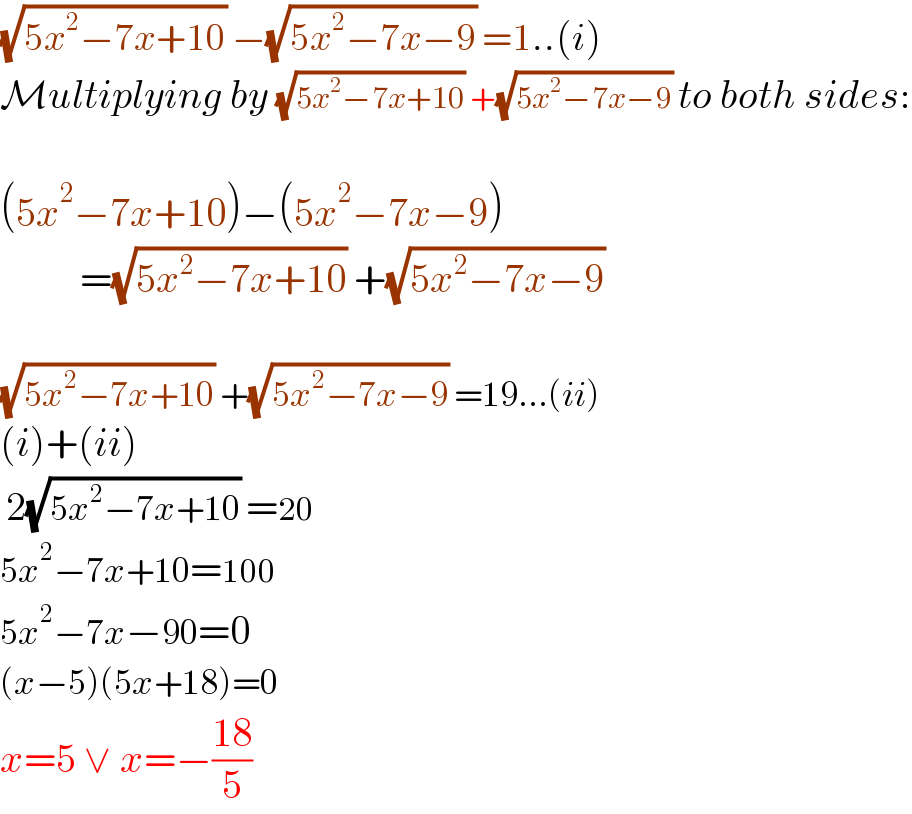
(√(5x^2 −7x+10)) −(√(5x^2 −7x−9)) =1..(i) Multiplying by (√(5x^2 −7x+10)) +(√(5x^2 −7x−9)) to both sides: (5x^2 −7x+10)−(5x^2 −7x−9) =(√(5x^2 −7x+10)) +(√(5x^2 −7x−9)) (√(5x^2 −7x+10)) +(√(5x^2 −7x−9)) =19...(ii) (i)+(ii) 2(√(5x^2 −7x+10)) =20 5x^2 −7x+10=100 5x^2 −7x−90=0 (x−5)(5x+18)=0 x=5 ∨ x=−((18)/5)

$$\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}}\:−\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{9}}\:=\mathrm{1}..\left({i}\right) \\ $$$$\mathcal{M}{ultiplying}\:{by}\:\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}}\:+\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{9}}\:{to}\:{both}\:{sides}: \\ $$$$ \\ $$$$\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}\right)−\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{9}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}}\:+\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{9}}\: \\ $$$$ \\ $$$$\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}}\:+\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{9}}\:=\mathrm{19}...\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right) \\ $$$$\:\mathrm{2}\sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}}\:=\mathrm{20} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{10}=\mathrm{100} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{90}=\mathrm{0} \\ $$$$\left({x}−\mathrm{5}\right)\left(\mathrm{5}{x}+\mathrm{18}\right)=\mathrm{0} \\ $$$${x}=\mathrm{5}\:\vee\:{x}=−\frac{\mathrm{18}}{\mathrm{5}}\: \\ $$

Commented by Michaelfaraday last updated on 31/Dec/22

thanks sir

$${thanks}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com