
Question Number 183845 by Michaelfaraday last updated on 30/Dec/22
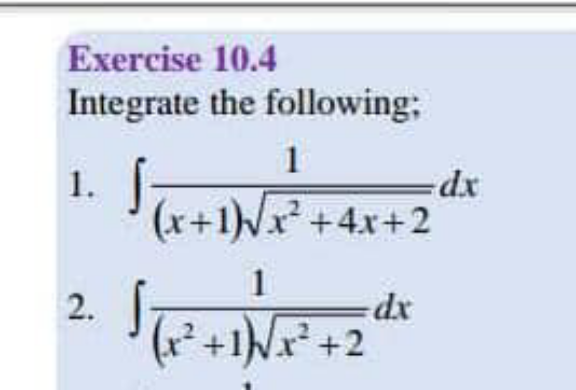
Answered by MJS_new last updated on 31/Dec/22
![∫(dx/((x+1)(√(x^2 +4x+2))))= [t=((x+2+(√(x^2 +4x+2)))/( (√2))) → dx=((√(x^2 +4x+2))/t)dt] =2∫(dt/( (√2)t^2 −2t+(√2)))=2arctan ((√2)t−1) = =2arctan (x+1+(√(x^2 +4x+2))) +C](Q183857.png)
$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}+\mathrm{2}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}}{{t}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{\:\sqrt{\mathrm{2}}{t}^{\mathrm{2}} −\mathrm{2}{t}+\sqrt{\mathrm{2}}}=\mathrm{2arctan}\:\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)\:= \\ $$$$=\mathrm{2arctan}\:\left({x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}\right)\:+{C} \\ $$
Answered by MJS_new last updated on 31/Dec/22
![∫(dx/((x^2 +1)(√(x^2 +2))))= [t=((x+(√(x^2 +2)))/( (√2))) → dx=((√(x^2 +2))/t)dx] =2∫(t/(t^4 +1))dt=arctan t^2 = =arctan (x^2 +1+x(√(x^2 +2))) +C](Q183858.png)
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}{{t}}{dx}\right] \\ $$$$=\mathrm{2}\int\frac{{t}}{{t}^{\mathrm{4}} +\mathrm{1}}{dt}=\mathrm{arctan}\:{t}^{\mathrm{2}} \:= \\ $$$$=\mathrm{arctan}\:\left({x}^{\mathrm{2}} +\mathrm{1}+{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\right)\:+{C} \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22

$${thanks}\:{sir} \\ $$
