
Question Number 183644 by mr W last updated on 28/Dec/22
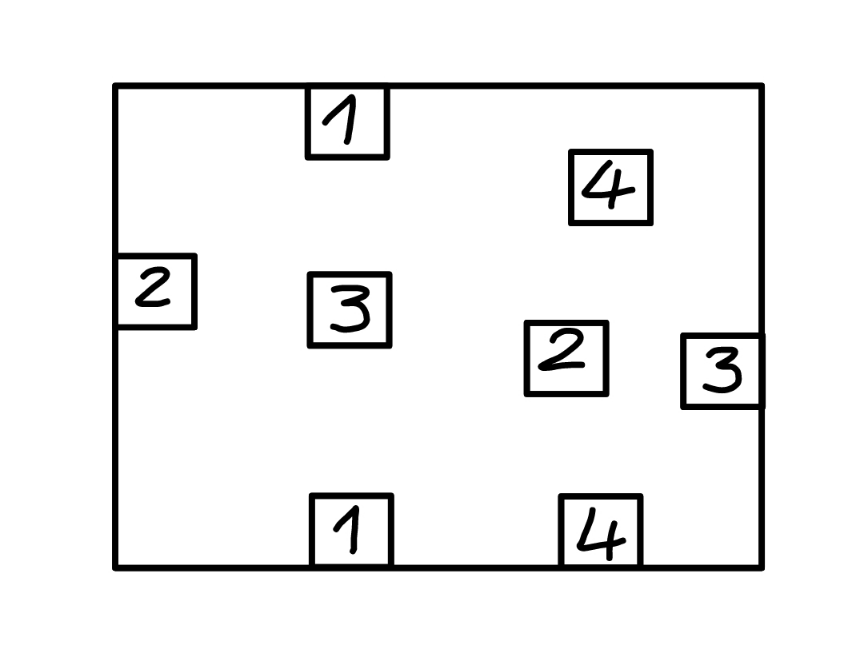
Commented by mr W last updated on 28/Dec/22

$${connect}\:{the}\:{boxes}\:{with}\:{same}\:{numbers}, \\ $$$${without}\:{leaving}\:{the}\:{board}\:{and}\:{without} \\ $$$${intersection}. \\ $$
Answered by qaz last updated on 28/Dec/22
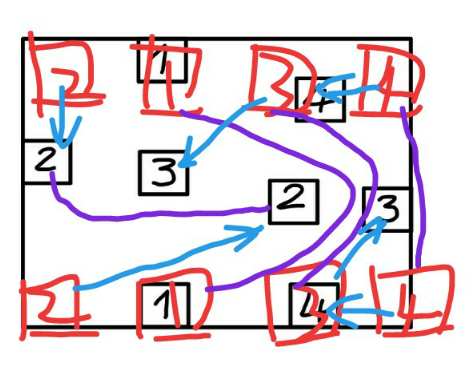
Answered by Rasheed.Sindhi last updated on 28/Dec/22

$${connect}\:\:{upper}\:\:{and}\:\:{lower}\:\:{edge}\:{in} \\ $$$${order}\:{to}\:{make}\:{the}\:{board}\:{horizontal} \\ $$$${cylinder}\:{with}\:{number}\:{outside}. \\ $$
Commented by Rasheed.Sindhi last updated on 28/Dec/22
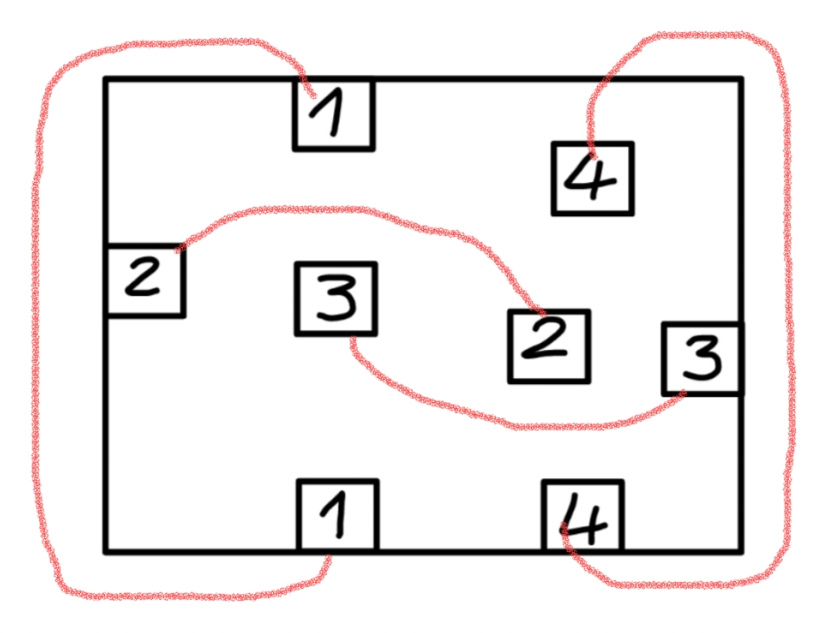
Commented by mr W last updated on 28/Dec/22

$${nice}\:{idea}! \\ $$$${but}\:{we}\:{have}\:\:{a}\:{hard}\:{board}\:{which}\:{can}\: \\ $$$${not}\:{be}\:{bent}.\:{just}\:{consider}\:{it}\:{as}\:{a}\:{IC}\: \\ $$$${board}\:{similarly}\:{like}\:{this}: \\ $$
Commented by mr W last updated on 28/Dec/22

Commented by Rasheed.Sindhi last updated on 28/Dec/22
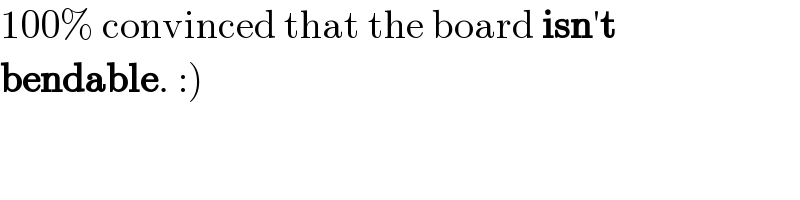
$$\mathrm{100\%}\:\mathrm{convinced}\:\mathrm{that}\:\mathrm{the}\:\mathrm{board}\:\boldsymbol{\mathrm{isn}}'\boldsymbol{\mathrm{t}} \\ $$$$\left.\boldsymbol{\mathrm{bendable}}.\::\right) \\ $$
Commented by Frix last updated on 28/Dec/22
$$\mathrm{Maybe}\:\mathrm{we}\:\mathrm{could}\:\mathrm{bend}\:\mathrm{the}\:\mathrm{space}\:\mathrm{around}\:\mathrm{it} \\ $$$$\mathrm{instead}? \\ $$
Commented by Rasheed.Sindhi last updated on 29/Dec/22
$${Nice}\:{idea}\:{sir}!\:{Only}\:{mathematician} \\ $$$${can}\:{think}\:{such}\:{ideas}. \\ $$
Answered by Rasheed.Sindhi last updated on 28/Dec/22
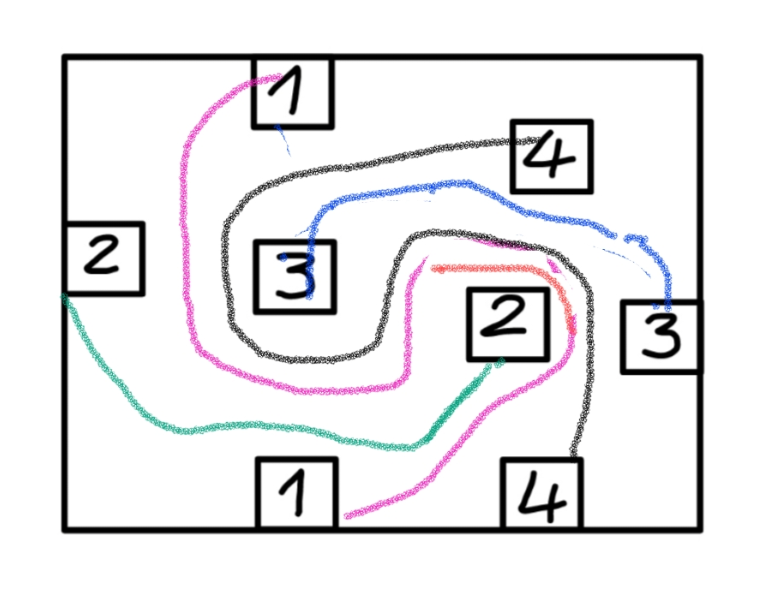
Commented by mr W last updated on 28/Dec/22

$${great}! \\ $$
Commented by mr W last updated on 28/Dec/22
$${an}\:{other}\:{possibility}: \\ $$
Commented by mr W last updated on 28/Dec/22
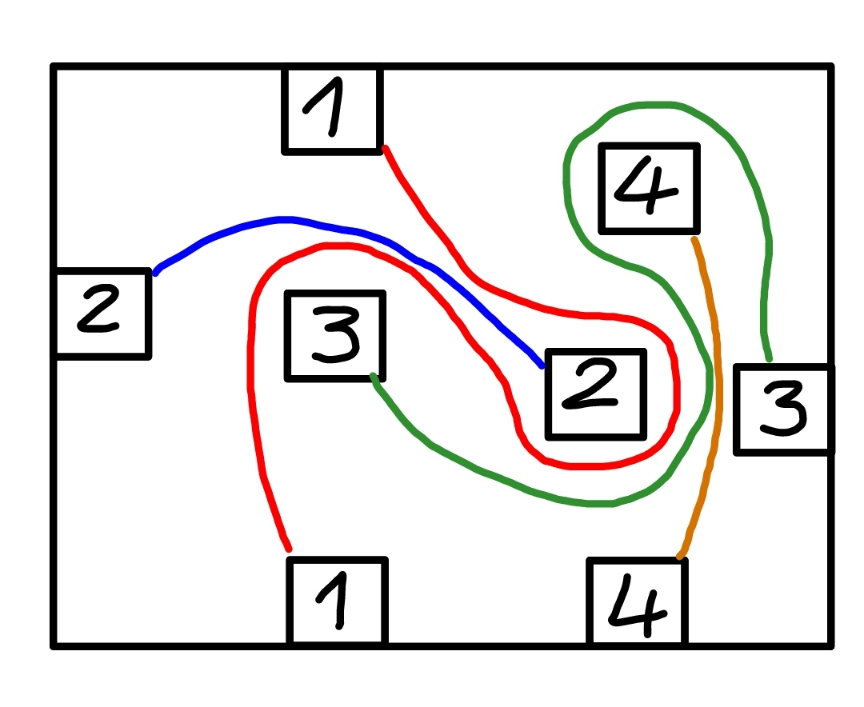
Commented by Rasheed.Sindhi last updated on 28/Dec/22

$$\mathcal{N}{ice}\:{sir}! \\ $$
Answered by MathematicalUser2357 last updated on 04/Nov/23

Sorry the image is too big
