Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 18342 by mondodotto@gmail.com last updated on 19/Jul/17

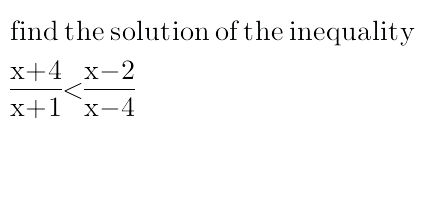
Answered by alex041103 last updated on 19/Jul/17

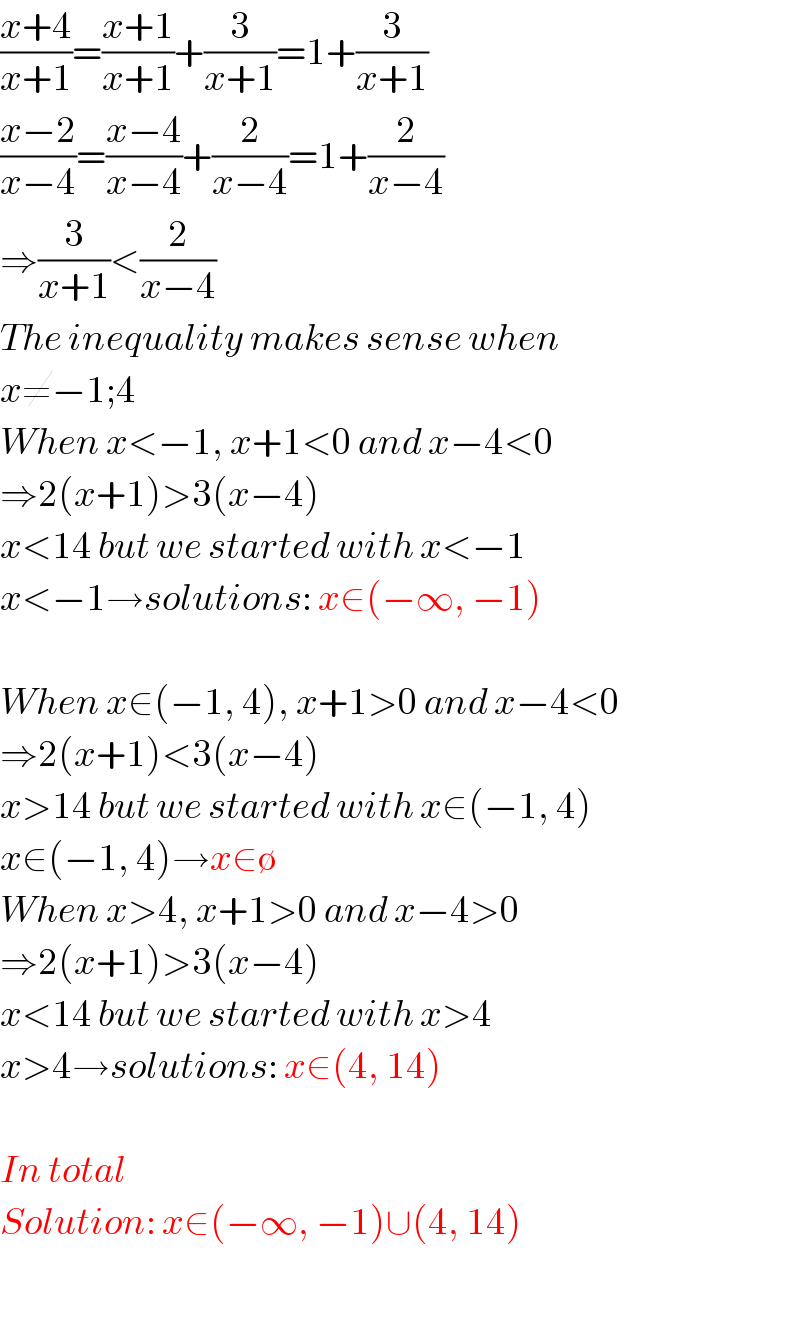
((x+4)/(x+1))=((x+1)/(x+1))+(3/(x+1))=1+(3/(x+1)) ((x−2)/(x−4))=((x−4)/(x−4))+(2/(x−4))=1+(2/(x−4)) ⇒(3/(x+1))<(2/(x−4)) The inequality makes sense when x≠−1;4 When x<−1, x+1<0 and x−4<0 ⇒2(x+1)>3(x−4) x<14 but we started with x<−1 x<−1→solutions: x∈(−∞, −1) When x∈(−1, 4), x+1>0 and x−4<0 ⇒2(x+1)<3(x−4) x>14 but we started with x∈(−1, 4) x∈(−1, 4)→x∈∅ When x>4, x+1>0 and x−4>0 ⇒2(x+1)>3(x−4) x<14 but we started with x>4 x>4→solutions: x∈(4, 14) In total Solution: x∈(−∞, −1)∪(4, 14)

$$\frac{{x}+\mathrm{4}}{{x}+\mathrm{1}}=\frac{{x}+\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{3}}{{x}+\mathrm{1}}=\mathrm{1}+\frac{\mathrm{3}}{{x}+\mathrm{1}} \\ $$$$\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}=\frac{{x}−\mathrm{4}}{{x}−\mathrm{4}}+\frac{\mathrm{2}}{{x}−\mathrm{4}}=\mathrm{1}+\frac{\mathrm{2}}{{x}−\mathrm{4}} \\ $$$$\Rightarrow\frac{\mathrm{3}}{{x}+\mathrm{1}}<\frac{\mathrm{2}}{{x}−\mathrm{4}} \\ $$$${The}\:{inequality}\:{makes}\:{sense}\:{when} \\ $$$${x}\neq−\mathrm{1};\mathrm{4} \\ $$$${When}\:{x}<−\mathrm{1},\:{x}+\mathrm{1}<\mathrm{0}\:{and}\:{x}−\mathrm{4}<\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left({x}+\mathrm{1}\right)>\mathrm{3}\left({x}−\mathrm{4}\right) \\ $$$${x}<\mathrm{14}\:{but}\:{we}\:{started}\:{with}\:{x}<−\mathrm{1} \\ $$$${x}<−\mathrm{1}\rightarrow{solutions}:\:{x}\in\left(−\infty,\:−\mathrm{1}\right) \\ $$$$ \\ $$$${When}\:{x}\in\left(−\mathrm{1},\:\mathrm{4}\right),\:{x}+\mathrm{1}>\mathrm{0}\:{and}\:{x}−\mathrm{4}<\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left({x}+\mathrm{1}\right)<\mathrm{3}\left({x}−\mathrm{4}\right) \\ $$$${x}>\mathrm{14}\:{but}\:{we}\:{started}\:{with}\:{x}\in\left(−\mathrm{1},\:\mathrm{4}\right) \\ $$$${x}\in\left(−\mathrm{1},\:\mathrm{4}\right)\rightarrow{x}\in\emptyset \\ $$$${When}\:{x}>\mathrm{4},\:{x}+\mathrm{1}>\mathrm{0}\:{and}\:{x}−\mathrm{4}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left({x}+\mathrm{1}\right)>\mathrm{3}\left({x}−\mathrm{4}\right) \\ $$$${x}<\mathrm{14}\:{but}\:{we}\:{started}\:{with}\:{x}>\mathrm{4} \\ $$$${x}>\mathrm{4}\rightarrow{solutions}:\:{x}\in\left(\mathrm{4},\:\mathrm{14}\right) \\ $$$$ \\ $$$${In}\:{total} \\ $$$${Solution}:\:{x}\in\left(−\infty,\:−\mathrm{1}\right)\cup\left(\mathrm{4},\:\mathrm{14}\right) \\ $$$$ \\ $$

Answered by ajfour last updated on 19/Jul/17

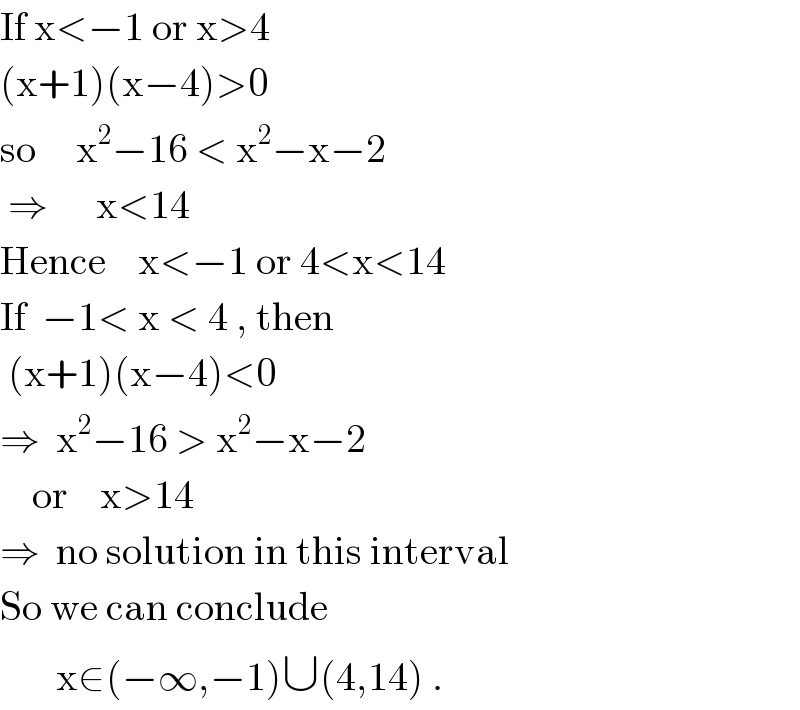
If x<−1 or x>4 (x+1)(x−4)>0 so x^2 −16 < x^2 −x−2 ⇒ x<14 Hence x<−1 or 4<x<14 If −1< x < 4 , then (x+1)(x−4)<0 ⇒ x^2 −16 > x^2 −x−2 or x>14 ⇒ no solution in this interval So we can conclude x∈(−∞,−1)∪(4,14) .

$$\mathrm{If}\:\mathrm{x}<−\mathrm{1}\:\mathrm{or}\:\mathrm{x}>\mathrm{4} \\ $$$$\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{4}\right)>\mathrm{0} \\ $$$$\mathrm{so}\:\:\:\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{16}\:<\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2} \\ $$$$\:\Rightarrow\:\:\:\:\:\:\mathrm{x}<\mathrm{14} \\ $$$$\mathrm{Hence}\:\:\:\:\mathrm{x}<−\mathrm{1}\:\mathrm{or}\:\mathrm{4}<\mathrm{x}<\mathrm{14} \\ $$$$\mathrm{If}\:\:−\mathrm{1}<\:\mathrm{x}\:<\:\mathrm{4}\:,\:\mathrm{then} \\ $$$$\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{4}\right)<\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{16}\:>\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2} \\ $$$$\:\:\:\:\mathrm{or}\:\:\:\:\mathrm{x}>\mathrm{14} \\ $$$$\Rightarrow\:\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{this}\:\mathrm{interval} \\ $$$$\mathrm{So}\:\mathrm{we}\:\mathrm{can}\:\mathrm{conclude} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}\in\left(−\infty,−\mathrm{1}\right)\cup\left(\mathrm{4},\mathrm{14}\right)\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com