
Question Number 183281 by mr W last updated on 24/Dec/22
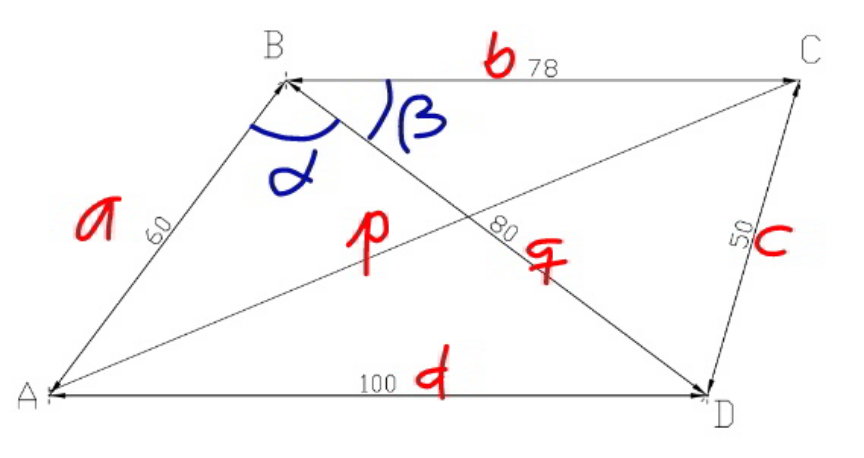
Commented by mr W last updated on 24/Dec/22

$${find}\:{the}\:{length}\:{of}\:{AC}. \\ $$
Answered by mr W last updated on 25/Dec/22
![cos α=((a^2 +q^2 −d^2 )/(2aq)) ⇒sin α=((√([q^2 −(a−d)^2 ][(a+d)^2 −q^2 ]))/(2aq)) cos β=((b^2 +q^2 −c^2 )/(2bq)) ⇒sin β=((√([q^2 −(b−c)^2 ][(b+c)^2 −q^2 ]))/(2bq)) p^2 =a^2 +b^2 −2ab cos (α+β) p^2 =a^2 +b^2 −2ab{((a^2 +q^2 −d^2 )/(2aq))×((b^2 +q^2 −c^2 )/(2bq))−((√([q^2 −(a−d)^2 ][(a+d)^2 −q^2 ]))/(2aq))×((√([q^2 −(b−c)^2 ][(b+c)^2 −q^2 ]))/(2bq))} p^2 =a^2 +b^2 −(((a^2 −d^2 +q^2 )(b^2 −c^2 +q^2 )−(√([(a+d)^2 −q^2 ][(a−d)^2 −q^2 ][(b+c)^2 −q^2 ][(b−c)^2 −q^2 ])))/(2q^2 )) p^2 =(((a^2 +b^2 +c^2 +d^2 −q^2 )q^2 −(a^2 −d^2 )(b^2 −c^2 )+(√([(a+d)^2 −q^2 ][(a−d)^2 −q^2 ][(b+c)^2 −q^2 ][(b−c)^2 −q^2 ])))/(2q^2 )) ⇒p=(1/q)(√(((a^2 +b^2 +c^2 +d^2 −q^2 )q^2 −(a^2 −d^2 )(b^2 −c^2 )+(√([(a+d)^2 −q^2 ][(a−d)^2 −q^2 ][(b+c)^2 −q^2 ][(b−c)^2 −q^2 ])))/2)) p=(1/(80))(√(((60^2 +78^2 +50^2 +100^2 −80^2 )×80^2 −(60^2 −100^2 )(78^2 −50^2 )+(√([(60+100)^2 −80^2 ][(60−100)^2 −80^2 ][(78+50)^2 −80^2 ][(78−50)^2 −80^2 ])))/2)) =30(√(17))≈123.693](Q183282.png)
$$\mathrm{cos}\:\alpha=\frac{{a}^{\mathrm{2}} +{q}^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{2}{aq}}\:\Rightarrow\mathrm{sin}\:\alpha=\frac{\sqrt{\left[{q}^{\mathrm{2}} −\left({a}−{d}\right)^{\mathrm{2}} \right]\left[\left({a}+{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]}}{\mathrm{2}{aq}} \\ $$$$\mathrm{cos}\:\beta=\frac{{b}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{bq}}\:\Rightarrow\mathrm{sin}\:\beta=\frac{\sqrt{\left[{q}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right]\left[\left({b}+{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]}}{\mathrm{2}{bq}} \\ $$$${p}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\left(\alpha+\beta\right) \\ $$$${p}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\left\{\frac{{a}^{\mathrm{2}} +{q}^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{2}{aq}}×\frac{{b}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{bq}}−\frac{\sqrt{\left[{q}^{\mathrm{2}} −\left({a}−{d}\right)^{\mathrm{2}} \right]\left[\left({a}+{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]}}{\mathrm{2}{aq}}×\frac{\sqrt{\left[{q}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right]\left[\left({b}+{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]}}{\mathrm{2}{bq}}\right\} \\ $$$${p}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\frac{\left({a}^{\mathrm{2}} −{d}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)−\sqrt{\left[\left({a}+{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({a}−{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({b}+{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({b}−{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]}}{\mathrm{2}{q}^{\mathrm{2}} } \\ $$$${p}^{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{q}^{\mathrm{2}} \right){q}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)+\sqrt{\left[\left({a}+{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({a}−{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({b}+{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({b}−{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]}}{\mathrm{2}{q}^{\mathrm{2}} } \\ $$$$\Rightarrow{p}=\frac{\mathrm{1}}{{q}}\sqrt{\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{q}^{\mathrm{2}} \right){q}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)+\sqrt{\left[\left({a}+{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({a}−{d}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({b}+{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\left[\left({b}−{c}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]}}{\mathrm{2}}} \\ $$$$ \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{80}}\sqrt{\frac{\left(\mathrm{60}^{\mathrm{2}} +\mathrm{78}^{\mathrm{2}} +\mathrm{50}^{\mathrm{2}} +\mathrm{100}^{\mathrm{2}} −\mathrm{80}^{\mathrm{2}} \right)×\mathrm{80}^{\mathrm{2}} −\left(\mathrm{60}^{\mathrm{2}} −\mathrm{100}^{\mathrm{2}} \right)\left(\mathrm{78}^{\mathrm{2}} −\mathrm{50}^{\mathrm{2}} \right)+\sqrt{\left[\left(\mathrm{60}+\mathrm{100}\right)^{\mathrm{2}} −\mathrm{80}^{\mathrm{2}} \right]\left[\left(\mathrm{60}−\mathrm{100}\right)^{\mathrm{2}} −\mathrm{80}^{\mathrm{2}} \right]\left[\left(\mathrm{78}+\mathrm{50}\right)^{\mathrm{2}} −\mathrm{80}^{\mathrm{2}} \right]\left[\left(\mathrm{78}−\mathrm{50}\right)^{\mathrm{2}} −\mathrm{80}^{\mathrm{2}} \right]}}{\mathrm{2}}} \\ $$$$\:\:=\mathrm{30}\sqrt{\mathrm{17}}\approx\mathrm{123}.\mathrm{693} \\ $$
Commented by manxsol last updated on 24/Dec/22
$${behold}\:{the}\:{surprise} \\ $$
Commented by manxsol last updated on 24/Dec/22
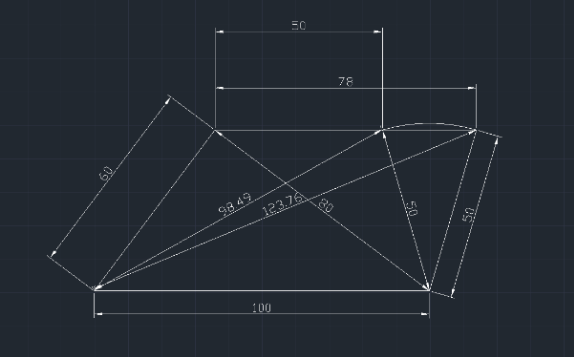
Commented by mr W last updated on 25/Dec/22
$${i}\:{can}'{t}\:{see}\:{what}\:{you}\:{meant}\:{with}\:{the} \\ $$$${surprise}.\:{you}\:{should}\:{specify}\:{what}\:{is} \\ $$$${given}\:{and}\:{what}\:{is}\:{to}\:{find}. \\ $$
Answered by Acem last updated on 24/Dec/22
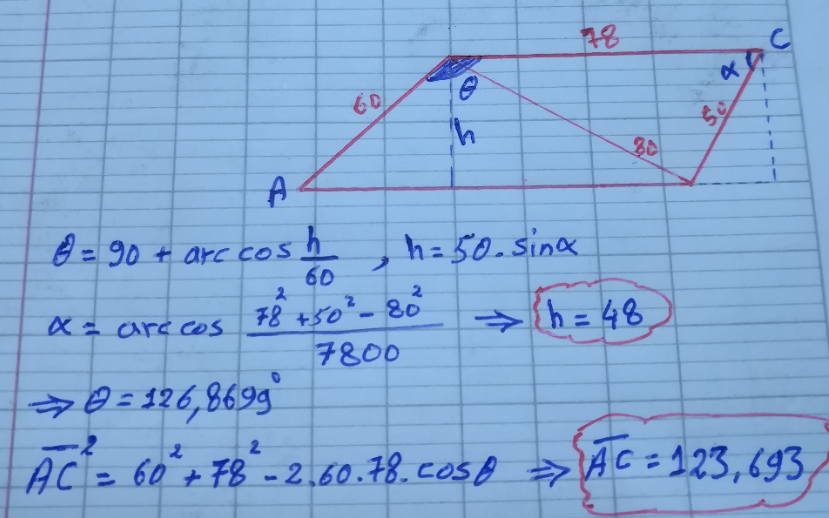
Commented by manxsol last updated on 25/Dec/22
$${if}\:{we}\:{put}\:{side}\:\mathrm{78}\:{unknown}\:;\:{we}\:{have}\:{two}\:{solution}\:\mathrm{123}\:{and}\:\mathrm{50}.\:{saludos}\:{Sir}\:{Acem} \\ $$
Commented by Acem last updated on 25/Dec/22

$${Saludos}\:{para}\:{ti}\:{mi}\:{querido}\:{amigo}! \\ $$
Commented by Acem last updated on 25/Dec/22
$${My}\:{friend},\:{did}\:{you}\:{mean}\:{that}\:{the}\:{side} \\ $$$$\:{BC}\:{is}\:{unknown}? \\ $$$$\:{if}\:{not},\:{then}\:{how}\:{will}\:{we}\:{have}\:{another}\:{solution} \\ $$$$\:{such}\:{AC}\:=\:\mathrm{50}? \\ $$
Commented by Acem last updated on 25/Dec/22

$$\:{Do}\:{you}\:{mean}\:{BC}=\:\mathrm{50}?\:{how}?\:{i}\:{saw}\:{your}\:{solution} \\ $$$$\:{but}\:{BC}\:{is}\:\mathrm{78}\:{and}\:{the}\:{question}\:{is}\:{to}\:{find}\:{AC} \\ $$$$\:{Well},\:{let}\:{me}\:{know}\:{what}\:{do}\:{you}\:{mean} \\ $$
